User Manual 4.7 Interpolation Methods : Différence entre versions
(Page créée avec « __NOTOC__ == Introduction == === Scope === In this section, a focus is realised on the following interpolation methods: spline, bicubic, tricubic, Lagrange and Newton, co... ») |
(Aucune différence)
|
Version actuelle en date du 7 mai 2021 à 07:34
Introduction
Scope
In this section, a focus is realised on the following interpolation methods: spline, bicubic, tricubic, Lagrange and Newton, covariance matrix and linear in 1D, 2D or 3D interpolation.
Javadoc
The interpolation objects are available in the package fr.cnes.sirius.patrius.math.analysis.interpolation and in the package fr.cnes.sirius.patrius.propagation.analytical.covariance.
Links
None as of now.
Useful Documents
None as of now.
Package Overview
The package fr.cnes.sirius.patrius.math.analysis.interpolation contains all the interpolation classes described in this section.
Features Description
Spline interpolation
The spline interpolator generates an interpolating function [math]f(x): \mathbb{R} \rightarrow \mathbb{R}[/math]. The user gives as entries 2 sets of values, the values of x, y. The interpolator gives the function f such as [math]y=f(x)[/math].
For the linear equation [math]y=2x+1[/math]
double x[] = { 0.0, 1.0, 2.0 }; double y[] = { 1.0, 3.0, 5.0 }; UnivariateInterpolator interpolator = new SplineInterpolator(); UnivariateFunction function = interpolator.interpolate(x, y); double value = function .value(0.5);
Bicubic interpolation
The bicubic interpolator generates an interpolating function [math]f(x,y): \mathbb{R}^2 \rightarrow \mathbb{R}[/math]. The interpolator computes internally the coefficients of the bicubic function that is the interpolating function. The user gives as entries 3 sets of values, the values of x, y and z. The interpolator gives the function f such as [math]z=f(x,y)[/math].
For the equation of the plane [math]z=2x-3y + 5[/math]
double x[] = { 3, 4, 5, 6.5 }; double y[] = {-4, -3, -1, 2, 2.5 }; double z[][] = {{ 23, 20, 14, 5, 3.5 }, { 25, 22, 16, 7, 5.5 }, { 27, 24, 18, 9, 7.5 }, { 30, 27, 21, 12, 10.5 }}; BivariateGridInterpolator interpolator = new BicubicSplineInterpolator(); BivariateFunction function = interpolator.interpolate(x, y, z);
Tricubic interpolation
The tricubic interpolator generates an interpolating function [math]f(x,y,z): \mathbb{R}^3 \rightarrow \mathbb{R}[/math]. The interpolator computes internally the coefficients of the tricubic function that is the interpolating function. The user gives as entries 4 sets of values, the values of x, y, z and w. The interpolator gives the function f such as [math]w=f(x,y,z)[/math].
For the equation of the plane [math]w=2x- 3y - z + 5[/math]
double x[] = { 3.0, 4.0, 5.0, 6.5 }; double y[] = {-4.0, -3.0, -1.0, 2.0, 2.5 }; double z[] = {-12.0, -8.0, -5.5, -3.0, 0.0, 2.5 }; double w[][][] = {{{ 35, 31, 28.5, 26, 23, 20.5 }, { 32, 28, 25.5, 23, 20, 17.5 }, { 26, 22, 19.5, 17, 14, 11.5 }, { 17, 13, 10.5, 8, 5, 2.5 }, { 15.5, 11.5, 9, 6.5, 3.5, 1 }}, {{ 37, 33, 30.5, 28, 25, 22.5 }, { 34, 30, 27.5, 25, 22, 19.5 }, { 28, 24, 21.5, 19, 16, 13.5 }, { 19, 15, 12.5, 10, 7, 4.7 }, { 17.5, 13.5, 11, 8.5, 5.5, 3 }}, {{ 39, 35, 32.5, 30, 27, 24.7 }, { 36, 32, 39.5, 27, 24, 21.5 }, { 30, 26, 23.5, 21, 18, 15.5 }, { 21, 17, 14.7, 12, 9, 6.5 }, { 19.5, 15.5, 13, 10.5, 7.5, 5 }}, {{ 42, 38, 35.5, 33, 30, 27.5 }, { 39, 35, 32.5, 30, 27, 24.7 }, { 33, 29, 26.5, 24, 21, 18.5 }, { 24, 20, 17.5, 15, 12, 9.5 }, { 22.5, 18.5, 16, 13.5, 10.5, 8 }}}; TrivariateGridInterpolator interpolator = new TricubicSplineInterpolator(); TrivariateFunction function = interpolator.interpolate(x, y, z, w);
Lagrange interpolation
The Lagrange interpolator generates an interpolating function [math]f(x): \mathbb{R} \rightarrow \mathbb{R}[/math]. The user gives as entries 2 sets of values, the values of x, y. The interpolator gives the function f such as [math]y=f(x)[/math].
For the linear equation [math]y=2x+1[/math]
double x[] = { 0.0, 1.0, 2.0 }; double y[] = { 1.0, 3.0, 5.0 }; UnivariateFunction interpolator = new PolynomialFunctionLagrangeForm(x,y); double value = interpolator.value(0.5);
Newton interpolation
The Newton interpolator generates an interpolating function [math]f(x): \mathbb{R} \rightarrow \mathbb{R}[/math]. The user gives as entries 2 sets of values, the coefficients [math]c_i[/math]and the centers [math]x_i[/math]such as the polynomial function [math]P(x)=c_0 + c_1 (x - x_0) + ... + c_n (x - x_n)[/math]. The interpolator gives the function f such as [math]y=P(x)[/math].
For the linear equation [math]y=2x+1[/math]
double c_i[] = { 3.0, 2.0 }; double x_i[] = { 1.0 }; UnivariateFunction interpolator = new PolynomialFunctionNewtonForm(c_i,x_i); double value = interpolator.value(0.5);
Covariance matrix interpolation
The purpose of this interpolation algorithm is to compute the covariance matrix at a given date through a simplified model of the transition matrix. When a covariance in PV coordinates is searched for an object orbiting around an celestial body, a simple dynamical model can be used, meaning limited to the newtonian attraction, plus a constant acceleration. The value of this constant acceleration will not change the transition matrix.
The transition matrix between a date [math]t_1[/math] and a date [math]t[/math] can be approximated :
- at order 0 : by [math]\phi_1(t_1, t) = I_{3 \times 3}[/math]
- at order 1 : by [math]\phi_1(t_1, t) = I_{3 \times 3} + J_{PV} ( t- t_1)[/math]
- at order 2 : by[math]\phi_1(t_1, t) =I_{3 \times 3} + J_{PV} ( t- t_1)+ 0.5 * J_{PV}^2 ( t - t_1)^2[/math]
where [math]J_{PV} = \left(\begin{array}{cc} 0_{3 \times 3} & I_{3 \times 3} \\ A & 0_{3 \times 3} \end{array} \right)[/math], [math]J_{PV}^2 = \left(\begin{array}{cc} A & 0_{3 \times 3} \\ 0_{3 \times 3} & A \end{array} \right)[/math] and [math]A =- \frac{ GM}{r^3}\left(I_{3 \times 3} - 3 \frac{ PP^T}{r^2}\right)[/math], where [math]A[/math] is considered as a constant on the interval [math][t_1,t][/math] and [math]P[/math] is the satellite position vector.
We denote by [math]M(t)[/math] the covariance matrix at instant t. Let [math]t \in [t_1,t][/math] . The transition matrices [math]\phi_1(t_1, t)[/math] and [math]\phi_2(t_2, t)[/math] are given by the above formula, and since matrix [math]A[/math] is constant on [math][t_1,t_2][/math], we have that the covariance matrix at instant [math]t[/math] is given by [math]M(t) = (1- \alpha) \phi_1(t_1, t) M(t_1)\phi_1^T(t_1, t) + \alpha \phi_2(t_2, t) M(t_2)\phi_2^T(t_2, t),[/math] with [math]\alpha = \frac{t-t_1}{t_2-t_1}[/math].
Linear interpolation
These classes allow linear piecewise interpolations in dimensions 1, 2 or 3.
1D interpolation
Let [math]f[/math] be a real function [math]\mathbb{R} \rightarrow \mathbb{R}[/math] and [math][x_1,x_2][/math] the interpolation interval, where [math]f(x_1),f(x_2)[/math] are known. For all [math]x \in [x_1,x_2][/math], the interpolated value [math]f(x)[/math] is given by [math]f(x) = f(x_1) + (x-x_1) \frac{f(x_2)- f(x_1)}{x_2-x_1}.[/math]
2D interpolation
The two dimensional interpolation will be two successive 1D interpolations. Let [math]f[/math] be a real function [math]\mathbb{R}^2 \rightarrow \mathbb{R}[/math] and [math][x_1,x_2] \times [y_1,y_2][/math] the interpolation interval. First, a 1D interpolation in the [math]y[/math] direction is made, leading to [math]f(x,y_1) = f(x_1,y_1) + (y-y_1) \frac{f(x_2,y_1)- f(x_1,y_1)}{y_2-y_1},[/math]
[math]f(x,y_2) = f(x_1,y_2) + (y-y_1) \frac{f(x_2,y_2)- f(x_1,y_2)}{y_2-y_1}.[/math]
Then a second 1D interpolation is made in the [math]x[/math] direction with the previous two interpolated values : [math]f(x,y) = f(x,y_1) + (x-x_1) \frac{f(x,y_2)- f(x, y_1)}{x_2-x_1}.[/math]
3D interpolation
Let [math]f[/math] be a real function [math]\mathbb{R}^3 \rightarrow \mathbb{R}[/math] and [math][x_1,x_2] \times [y_1,y_2] \times [z_1,z_2][/math] the interpolation interval. There will be [math]2^3- 1[/math] successives 1D interpolations.
[math]f(x,y,z)[/math] is interpolated from [math]f(x,y,z_1)[/math] and [math]f(x,y,z_2)[/math].
[math]f(x,y,z_1)[/math] is interpolated from [math]f(x,y_1,z_1)[/math] and [math]f(x,y_2,z_1)[/math].
[math]f(x,y,z_2)[/math] is interpolated from [math]f(x,y_1,z_2)[/math] and [math]f(x,y_2,z_2)[/math].
[math]f(x,y_1,z_1)[/math] is interpolated from [math]f(x_1,y_1,z_1)[/math] and [math]f(x_2,y_1,z_1)[/math].
[math]f(x,y_2,z_1)[/math] is interpolated from [math]f(x_1,y_2,z_1)[/math] and [math]f(x_2,y_2,z_1)[/math].
[math]f(x,y_1,z_2)[/math] is interpolated from [math]f(x_1,y_1,z_2)[/math] and [math]f(x_2,y_1,z_1)[/math].
[math]f(x,y_2,z_2)[/math] is interpolated from [math]f(x_1,y_2,z_2)[/math] and [math]f(x_2,y_2,z_2)[/math].
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
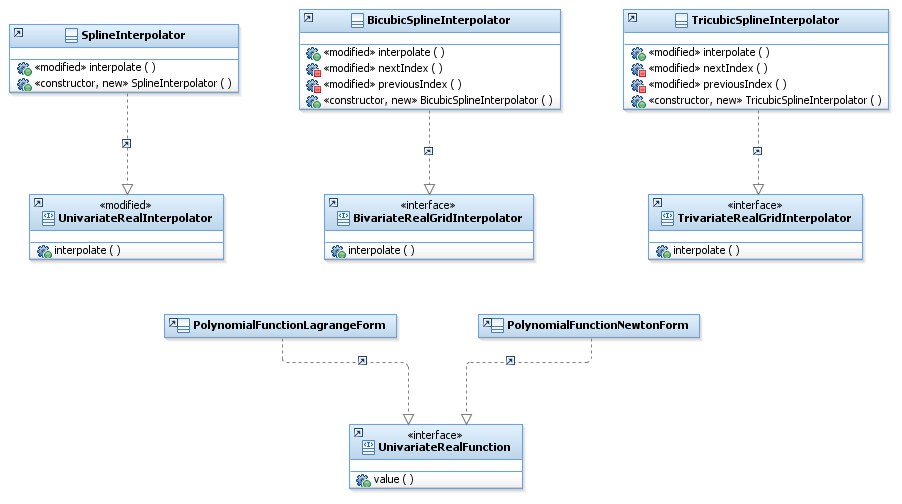
Interfaces
The library defines the following interfaces related to interpolation :
| Interface | Summary | Javadoc |
|---|---|---|
| UnivariateInterpolator | Interface for a univariate interpolating function. | ... |
| BivariateGridInterpolator | Interface for a bivariate interpolating function where the sample points must be specified on a regular grid. | ... |
| TrivariateGridInterpolator | Interface for a trivariate interpolating function where the sample points must be specified on a regular grid. | ... |
| UnivariateFunction | Interface for a univariate function | ... |
Classes
This section is about the following classes related to interpolation :
| Class | Summary | Javadoc |
|---|---|---|
| SplineInterpolator | Spline interpolator for a univariate real function. | ... |
| BicubicSplineInterpolator | Bicubic spline interpolator for a bivariate real function. | ... |
| TricubicSplineInterpolator | Tricubic spline interpolator for a trivariate real function. | ... |
| PolynomialFunctionLagrangeForm | Lagrange interpolator, directly usable as a univariate real function. | ... |
| PolynomialFunctionNewtonForm | Newton interpolator, directly usable as a univariate real function. | ... |
| Class | Summary | Javadoc |
|---|---|---|
| CovarianceInterpolation | Interpolator of a covariance matrix based on its two surrounding covariance matrices. | ... |
| OrbitCovariance | Class containing a covariance matrix and its associated AbsoluteDate. New class replacing older class CovarianceMatrix | ... |
| Class | Summary | Javadoc |
|---|---|---|
| CovarianceInterpolation | Interpolator of a covariance matrix based on its two surrounding covariance matrices. | ... |
| OrbitCovariance | Class containing a covariance matrix and its associated AbsoluteDate. New class replacing older class CovarianceMatrix | ... |
| Class | Summary | Javadoc |
|---|---|---|
| AbstractLinearIntervalsFunction | Abstract class for linear interpolations. | ... |
| UniLinearIntervalsFunction | Linear one-dimensional function. | ... |
| BiLinearIntervalsFunction | Linear two-dimensional function. | ... |
| TriLinearIntervalsFunction | Linear three-dimensional function. | ... |
| UniLinearIntervalsInterpolator | Interpolator of linear one-dimensional functions. | ... |
| BiLinearIntervalsInterpolator | Interpolator of linear two-dimensional functions. | ... |
| TriLinearIntervalsInterpolator | Interpolator of linear three-dimensional functions. | ... |