User Manual 3.3 Numerical ordinary differential equations
Sommaire
Introduction
Scope
This library can compute solutions for ordinary differential equations, as numerical approximations. The problems are usually in the form of : Compute an estimate of y(t) from t=t0 to t=t1, knowing the derivative y'=f(t,y), and y(t0)=y0.
The library can also handle multiple discrete events detection based on the results of the ongoing estimation, which can be used to dynamically alter the conditions of the problem being solved, or even stop the integration (for instance : when the function y reaches an expected value, the value of t at this point being the information needed, there is no need to go on).
IMPORTANT : these functionalities are all provided by the underlying Apache Commons Math library. Therefore, this section will focus on general usability, and will point to existing (mainly Javadoc) documentation for the specifics. The only addition to the Commons Math library is the 6^^th^^ order Runge-Kutta integrator that derives from the general RungeKutta classes.
Javadoc
Integrators
The ODE integrators are provided in the following packages :
| Library | Javadoc |
|---|---|
| Commons Math | Package org.apache.commons.math3.ode |
| Commons Math | Package org.apache.commons.math3.ode.nonstiff |
| Commons Math | Package org.apache.commons.math3.ode.sampling |
Event handling
The events are managed in the following package :
| Library | Javadoc |
|---|---|
| Commons Math | Package org.apache.commons.math3.ode.events |
Links
None as of now.
Useful Documents
A general purpose explanation of this section can be found here :
http://en.wikipedia.org/wiki/Numerical_ordinary_differential_equations
Package Overview
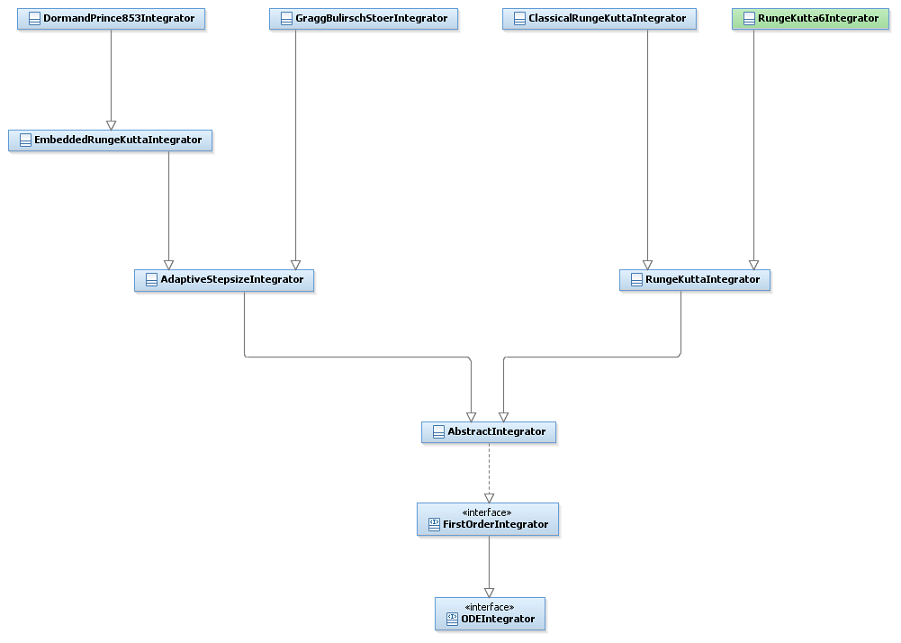
Integrators :
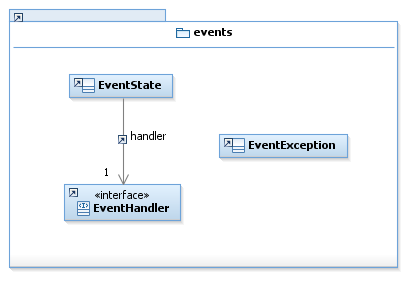
Events package :
Features Description
Integrators
The integrators provided by the Commons Math project include :
- the Classical Runge Kutta integrator,
- the Dormand Prince 8(5, 3) integrator and
- the Gragg Bulirsch Stoer integrator.
An additional integrator has been included in Commons Math Addons :
- the 6^^th^^ order Runge-Kutta integretor.
The ODE package documentation can be found Modèle:SiteLink label="here" jd="CM" suffix="userguide/ode.html"/.
Events
Event handling during an integrator run is a core functionality of the underlying Apache Commons Math library, therefore this is already well-documented in the Javadoc (please see the relevant section). This here is a short summary of how event handling works.
How to monitor events
*create an EventHandler implementation
You need to create an EventHandler implementation for the event you want to trace.
The most important method here is the g() method :
double g(double t, double[] y) throws EventException;
This method (which takes as input a solution of the integration problem at a given "time" t) should be designed so thatwhen the event occurs, the sign of the method changes. It should also be continuous.
The other methods of the interface are :
-
int eventOccurred(double t,
double[] y, boolean increasing, boolean forward)
throws EventException;This method is called when an event happens. It should return :
- STOP if the integration computation should stop
- RESET_STATE if the event handler wants to change the state vector before the integration resumes (the resetState method will be called)
- RESET_DERIVATIVES if the state vector's derivatives need to be recomputed before the integration resumes
- CONTINUE if the integration should continue as if nothing happened
-
void resetState(double t, double[] y) throws EventException
This method is called when eventOccured has returned RESET_STATE. This method should modify the y array, which will change the way the integration performs.
*add the EventHandler to an appropriate integrator Using an EventHandler on a given integration problem is simple : just add it to the integrator instance before computing the solution.
integrator.addEventHandler(eventHandler, maxCheckInterval, convergence, maxIterationCount);Aside from the EventHandler itself, the other parameters are :- maxCheckInterval : Maximal time interval between events handler checks.
- convergence : precision needed for the event "time" value.
- iterationCount : maximum number of iterations to find the event "time" value when an event has been identified. Reaching this number means there is a problem with finding the event quickly enough (so, this counter is a way to interrupt an event search that takes too long, since finding an event should be fast if the g() function is continuous).
*run the integrator Please see the relevant section.
About the EventState class
The EventState class is a very important class for event detection (one EventState instance is needed for each EventHandler to work), but since the integrator instantiates EventStates when needed, a regular user never needs to interact directy with an EventState object. Therefore, describing the EventState class is out of the scope of this document; all relevant information can be found in the Javadoc if needed.
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
Interfaces
|=(% colspan="3" %)Interface|=(% colspan="6" %)Summary|=Javadoc |(% colspan="3" %)FirstOrderIntegrator|(% colspan="6" %)This interface represents a first order integrator for differential equations.|... |(% colspan="3" %)ODEIntegrator|(% colspan="6" %)This interface defines the common parts shared by integrators for first and second order differential equations.|...
|=(% colspan="3" %)Interface|=(% colspan="6" %)Summary|=Javadoc |(% colspan="3" %)EventHandler|(% colspan="6" %)This interface represents a handler for discrete events triggered during ODE integration.|...
Classes
|=(% colspan="3" %)Interface|=(% colspan="6" %)Summary|=Javadoc |(% colspan="3" %)AbstractIntegrator|(% colspan="6" %)Base class managing common boilerplate for all integrators.|... |(% colspan="3" %)AdaptiveStepsizeIntegrator|(% colspan="6" %)This abstract class holds the common part of all adaptive stepsize integrators for Ordinary Differential Equations.|... |(% colspan="3" %)ClassicalRungeKuttaIntegrator|(% colspan="6" %)This class implements the classical fourth order Runge-Kutta integrator for Ordinary Differential Equations (it is the most often used Runge-Kutta method).|... |(% colspan="3" %)RungeKutta6Integrator|(% colspan="6" %)This class implements the sixth order Runge-Kutta integrator for Ordinary Differential Equations (it is used as the default Stela Integretor). Warning: this integrator currently has an underlying linear step interpolator.|... |(% colspan="3" %)DormandPrince54Integrator|(% colspan="6" %)This class implements the 5(4) Dormand-Prince integrator for Ordinary Differential Equations.|... |(% colspan="3" %)DormandPrince853Integrator|(% colspan="6" %)This class implements the 8(5,3) Dormand-Prince integrator for Ordinary Differential Equations.|... |(% colspan="3" %)GraggBulirschStoerIntegrator|(% colspan="6" %)This class implements a Gragg-Bulirsch-Stoer integrator for Ordinary Differential Equations.|... |(% colspan="3" %)RungeKuttaIntegrator|(% colspan="6" %)This class implements the common part of all fixed step Runge-Kutta integrators for Ordinary Differential Equations.|...
|=(% colspan="3" %)Interface|=(% colspan="6" %)Summary|=Javadoc |(% colspan="3" %)EventState|(% colspan="6" %)This class handles the state for one EventHandler during integration steps.|...
Tutorials
Tutorial 1
Modèle:SpecialInclusion prefix=$theme sub section="Tuto1"/
Tutorial 2
Modèle:SpecialInclusion prefix=$theme sub section="Tuto2"/
 Tips & Tricks
Tips & Tricks
-