« User Manual 3.3 Kinematics » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| (7 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 8 : | Ligne 8 : | ||
The kinematics objects are available in the package org.orekit.attitudes.kinematics in the Orekit library. | The kinematics objects are available in the package org.orekit.attitudes.kinematics in the Orekit library. | ||
|= | {| class="wikitable" | ||
| | |- | ||
! scope="col"| Library | |||
! scope="col"| Javadoc | |||
|- | |||
|Orekit | |||
|[{{JavaDoc3.3}}/org/orekit/attitudes/kinematics/package-summary.html Package org.orekit.attitudes.kinematics] | |||
|} | |||
=== Links === | === Links === | ||
| Ligne 19 : | Ligne 25 : | ||
=== Package Overview === | === Package Overview === | ||
The following diagram represents the main classes of the <code>org.orekit.attitudes.kinematics</code> package: | The following diagram represents the main classes of the <code>org.orekit.attitudes.kinematics</code> package: | ||
[[File:kinematics.png|center]] | |||
== Features Description == | == Features Description == | ||
| Ligne 27 : | Ligne 32 : | ||
A quaternion can be differentiated using various methods: | A quaternion can be differentiated using various methods: | ||
* The quaternion differentiation’s formula <math>\ | * The quaternion differentiation’s formula <math>\dot{Q}_{S/R} = \frac{1}{2}Q_{S/R}\Omega_{S/R}^{[S]}</math>. | ||
This formula connects time derivative of the quaternion q(t) with the vector of angular velocity W(t). | |||
* When the quaternion is represented by a set of differentiable functions (Fourier series or polynomials), a direct analytic computation can be performed to get its derivative; | * When the quaternion is represented by a set of differentiable functions (Fourier series or polynomials), a direct analytic computation can be performed to get its derivative; | ||
| Ligne 47 : | Ligne 52 : | ||
* compute the spin from the Euler or Cardan angles and their derivatives; | * compute the spin from the Euler or Cardan angles and their derivatives; | ||
* using a direct analytic computation (when the function representing its variation over time is available). | * using a direct analytic computation (when the function representing its variation over time is available). | ||
=== Time-dependent orientation function=== | === Time-dependent orientation function=== | ||
| Ligne 72 : | Ligne 62 : | ||
* return the function representing the derivative of the quaternion components, by the <code>derivative()</code> method. A numerical differentiation method is used to compute the derivatives, nevertheless the classes inheriting the <code>AbstractOrientationFunction</code> can override this method and return the analytical function representing the derivatives, when possible. | * return the function representing the derivative of the quaternion components, by the <code>derivative()</code> method. A numerical differentiation method is used to compute the derivatives, nevertheless the classes inheriting the <code>AbstractOrientationFunction</code> can override this method and return the analytical function representing the derivatives, when possible. | ||
* compute the function representing the spin using the <math>\Omega_{S/R}^{[S]} = 2Q_{S/R}\ | * compute the function representing the spin using the <math>\Omega_{S/R}^{[S]} = 2Q_{S/R}\dot{Q}_{S/R}</math> formula, by the <code>computeSpinFunction()</code> method. The derivatives of the quaternion are computed thanks to the <code>derivative()</code> method. | ||
* estimate the function representing the spin using two rotations corresponding to two different dates (the velocity is supposed to be constant during the time interval between the two rotations), by the <code>estimateRateFunction(dt)</code> method. | * estimate the function representing the spin using two rotations corresponding to two different dates (the velocity is supposed to be constant during the time interval between the two rotations), by the <code>estimateRateFunction(dt)</code> method. | ||
| Ligne 95 : | Ligne 85 : | ||
As a time-dependent quaternion can be represented by the <code>OrientationFunction</code> interface, the derivative of the quaternion can be computed using the <code>derivative()</code> method. As this method is implemented by the user, he can choose to use a numerical differentiation method or to compute the exact derivative, when possible. | As a time-dependent quaternion can be represented by the <code>OrientationFunction</code> interface, the derivative of the quaternion can be computed using the <code>derivative()</code> method. As this method is implemented by the user, he can choose to use a numerical differentiation method or to compute the exact derivative, when possible. | ||
The derivative of a quaternion can be also computed using the kinematics equation: <math>\ | The derivative of a quaternion can be also computed using the kinematics equation: <math>\dot{Q}_{S/R} = \frac{1}{2}Q_{S/R}\Omega_{S/R}^{[S]}</math>. | ||
This equation is implemented by the following method in the kinematics toolkit: | This equation is implemented by the following method in the kinematics toolkit: | ||
< | |||
<syntaxhighlight lang="java">public static Quaternion differentiateQuaternion(final Quaternion q, final Vector3D spin)</syntaxhighlight> | |||
=== Integrate a quaternion === | === Integrate a quaternion === | ||
| Ligne 126 : | Ligne 117 : | ||
* Estimation: two rotations corresponding to two different dates are used to compute the spin (the velocity is supposed to be constant during the time interval between the two rotations). | * Estimation: two rotations corresponding to two different dates are used to compute the spin (the velocity is supposed to be constant during the time interval between the two rotations). | ||
This function is implemented by the following method in the kinematics toolkit: | This function is implemented by the following method in the kinematics toolkit: | ||
* <math>\Omega_{S/R}^{[S]} = 2Q_{S/R}\ | <syntaxhighlight lang="java">public static Vector3D estimateSpin(final Rotation start, final Rotation end, final double dt)</syntaxhighlight>. | ||
* <math>\Omega_{S/R}^{[S]} = 2Q_{S/R}\dot{Q}_{S/R}</math>, when knowing the derivative of the quaternion. | |||
This equation is implemented by the following kinematics toolkit method: | This equation is implemented by the following kinematics toolkit method: | ||
< | |||
<syntaxhighlight lang="java">public static Vector3D computeSpin(final Quaternion q, final Quaternion qd)</syntaxhighlight>. | |||
* Using the derivative of the Euler or Cardan angles: | * Using the derivative of the Euler or Cardan angles: | ||
** Euler (not to be used when the angles are small): | ** Euler (not to be used when the angles are small): | ||
<math>\Omega_{S/R}^{[S]} = \left[ \begin{array}{c} \dot{\psi}\sin(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\sin(\theta)\cos(\phi)- \dot{\theta}\sin(\phi) \\ \dot{\psi}\cos(\theta) + \dot{\phi} \end{array} \right]</math> | <math>\Omega_{S/R}^{[S]} = \left[ \begin{array}{c} \dot{\psi}\sin(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\sin(\theta)\cos(\phi)- \dot{\theta}\sin(\phi) \\ \dot{\psi}\cos(\theta) + \dot{\phi} \end{array} \right]</math> | ||
** Cardan (only to be used when the angles are small): | ** Cardan (only to be used when the angles are small): | ||
<math>\Omega_{S/R}^{[S]} = \left[ \begin{array}{c}-\dot{\psi}\sin(\theta)+\dot{\phi} \\ \dot{\psi}\cos(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\cos(\theta)\cos(\phi) - \dot{\theta}\sin(\phi) \end{array} \right]</math> | <math>\Omega_{S/R}^{[S]} = \left[ \begin{array}{c}-\dot{\psi}\sin(\theta)+\dot{\phi} \\ \dot{\psi}\cos(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\cos(\theta)\cos(\phi) - \dot{\theta}\sin(\phi) \end{array} \right]</math> | ||
These formula are implemented by the following kinematics toolkit method: | These formula are implemented by the following kinematics toolkit method: | ||
< | |||
<syntaxhighlight lang="java">public static Vector3D computeSpin(final double[] ang, final double[] angd, final RotationOrder order)</syntaxhighlight>. | |||
* Analytic computation: if the spin is represented by a function, its instantaneous value must be obtained by direct analytic computation (the <code>IVector3DFunction</code> classes have been created for this purpose) | * Analytic computation: if the spin is represented by a function, its instantaneous value must be obtained by direct analytic computation (the <code>IVector3DFunction</code> classes have been created for this purpose) | ||
== Getting Started == | |||
TBD | |||
== Contents == | |||
=== Interfaces === | |||
{| class="wikitable" | |||
|- | |||
! scope="col"| Interface | |||
! scope="col"| Summary | |||
! scope="col"| Javadoc | |||
|- | |||
|'''OrientationFunction''' | |||
|This interface represents a generic univariate orientation function. | |||
|[{{JavaDoc3.3}}/org/orekit/attitudes/kinematics/OrientationFunction.html ...] | |||
|- | |||
|'''Vector3DFunction''' | |||
|This interface represents a generic univariate 3-D vector function. | |||
|[{{JavaDoc3.3}}/org/orekit/attitudes/kinematics/Vector3DFunction.html ...] | |||
|} | |||
=== Classes === | |||
{| class="wikitable" | |||
|- | |||
! scope="col"| Class | |||
! scope="col"| Summary | |||
! scope="col"| Javadoc | |||
|- | |||
|'''AbstractOrientationFunction''' | |||
|This class represents an orientation function. | |||
|[{{JavaDoc3.3}}/org/orekit/attitudes/kinematics/AbstractOrientationFunction.html ...] | |||
|- | |||
|'''AbstractVector3DFunction''' | |||
|This class represents a spin function, or a spin n-th derivative function. | |||
|[{{JavaDoc3.3}}/org/orekit/attitudes/kinematics/AbstractVector3DFunction.html ...] | |||
|} | |||
== Tutorials == | == Tutorials == | ||
| Ligne 151 : | Ligne 183 : | ||
== [[File:lightBulb.png]] Tips & Tricks == | == [[File:lightBulb.png]] Tips & Tricks == | ||
{{specialInclusion prefix=$theme_sub section="Tips"/}} | {{specialInclusion prefix=$theme_sub section="Tips"/}} | ||
[[Category:User_Manual_3.3_Attitude]] | |||
Dernière version du 26 février 2018 à 16:53
Introduction
Scope
The purpose is to extend the current Orekit attitude package with classes and methods to compute and process kinematics operations.
Javadoc
The kinematics objects are available in the package org.orekit.attitudes.kinematics in the Orekit library.
| Library | Javadoc |
|---|---|
| Orekit | Package org.orekit.attitudes.kinematics |
Links
Modèle:SpecialInclusion prefix=$theme sub section="Links"/
Useful Documents
Modèle:SpecialInclusion prefix=$theme sub section="UsefulDocs"/
Package Overview
The following diagram represents the main classes of the org.orekit.attitudes.kinematics package:
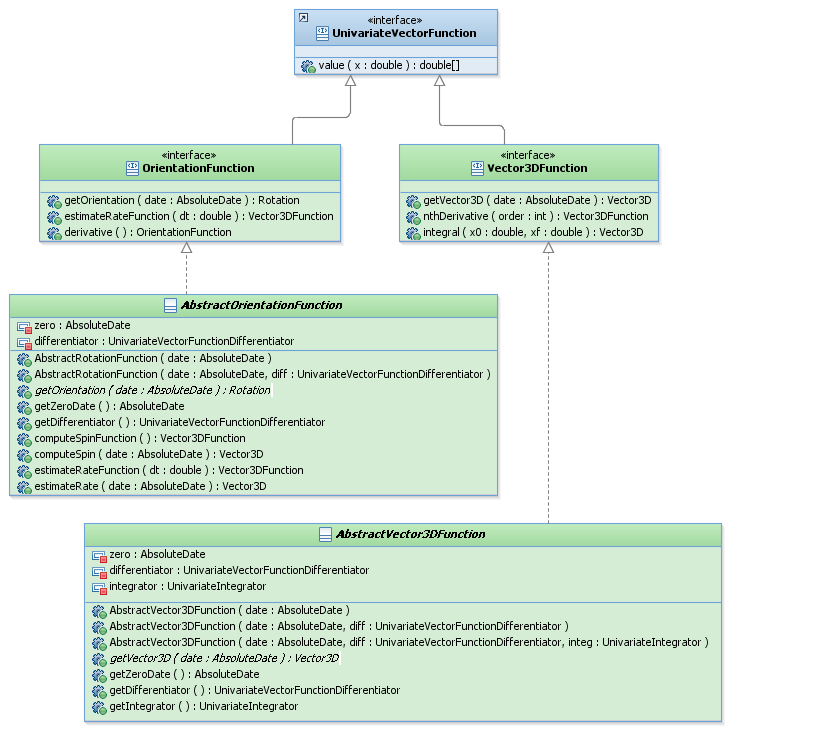
Features Description
Quaternions differentiation
A quaternion can be differentiated using various methods:
- The quaternion differentiation’s formula [math]\displaystyle{ \dot{Q}_{S/R} = \frac{1}{2}Q_{S/R}\Omega_{S/R}^{[S]} }[/math].
This formula connects time derivative of the quaternion q(t) with the vector of angular velocity W(t).
- When the quaternion is represented by a set of differentiable functions (Fourier series or polynomials), a direct analytic computation can be performed to get its derivative;
- Numerical differentiation (using finite difference, Ridders differentiation method, ...)
Quaternion integration
A rotation can be integrated, knowing its spin time function, using these methods:
- Wilcox method, with available approximations orders 1 to 4
- Edwards method, that corresponds to an order 3 approximation
Spin computation
The spin can be represented by a vector (instantaneous spin), or by a time-dependent function. The computation of the instantanous value of the spin can be made by one of the following methods:
- estimate the spin from two rotations corresponding to two different dates;
- using the kinematics equation when a quaternion and its derivative are known;
- compute the spin from the Euler or Cardan angles and their derivatives;
- using a direct analytic computation (when the function representing its variation over time is available).
Time-dependent orientation function
The interface OrientationFunction and the abstract class AbstractOrientationFunction have been added to the kinematics package in order to represent a time-dependent orientation function.
These classes provide the following functionalities:
- return the orientation at a date, by the
getOrientation(AbsoluteDate)method; it is an abstract method because it is specific to the orientation (or attitude) law the user wants to implement;
- return the function representing the derivative of the quaternion components, by the
derivative()method. A numerical differentiation method is used to compute the derivatives, nevertheless the classes inheriting theAbstractOrientationFunctioncan override this method and return the analytical function representing the derivatives, when possible.
- compute the function representing the spin using the [math]\displaystyle{ \Omega_{S/R}^{[S]} = 2Q_{S/R}\dot{Q}_{S/R} }[/math] formula, by the
computeSpinFunction()method. The derivatives of the quaternion are computed thanks to thederivative()method.
- estimate the function representing the spin using two rotations corresponding to two different dates (the velocity is supposed to be constant during the time interval between the two rotations), by the
estimateRateFunction(dt)method.
- return the spin at a date, by the
computeSpin(AbsoluteDate), orestimateRate(AbsoluteDate, dt)methods (they call thecomputeSpinFunction()andestimateRateFunction(dt)methods)
Time-dependent spin function
The interface Vector3DFunction and the abstract class AbstractVector3DFunction have been added to the kinematics package in order to represent a time-dependent vector 3D function; a vector 3D function is used to represent the spin, or the n-th derivative of the spin.
These classes provide the following functionalities:
- return the vector at a date, by the
getVector3D(AbsoluteDate)method; it is an abstract method because it is specific to the spin (or derivative of the spin) the user wants to implement;
- return the function representing the n-th derivative of the vector, by the
nthDerivative(order)method. A numerical differentiation method is used to compute the derivatives, nevertheless the classes inheriting theAbstractVector3DFunctioncan override this method and return the analytical function representing the derivatives, when possible.
This method uses the Commons Math classes contained in the differentiation package, in particular the DerivativeStructure class, which allows to compute the n-th derivatives of a function at a point;
- return the integral of the function by the
integral(x0, xf)method. A numerical integration method is used to compute the integral, nevertheless the classes inheriting theAbstractVector3DFunctioncan override this method and return the analytical function representing the integral, when possible.
The DynamicsElements object is created from a spin function and it gathers the n-th derivatives of spin at a given date; an attribute of this class is contained in the Attitude class.
Differentiate a quaternion
As a time-dependent quaternion can be represented by the OrientationFunction interface, the derivative of the quaternion can be computed using the derivative() method. As this method is implemented by the user, he can choose to use a numerical differentiation method or to compute the exact derivative, when possible.
The derivative of a quaternion can be also computed using the kinematics equation: [math]\displaystyle{ \dot{Q}_{S/R} = \frac{1}{2}Q_{S/R}\Omega_{S/R}^{[S]} }[/math]. This equation is implemented by the following method in the kinematics toolkit:
public static Quaternion differentiateQuaternion(final Quaternion q, final Vector3D spin)
Integrate a quaternion
The rotation integration is to be made by the following methods of the KinematicsToolkit class :
- Wilcox method :
Rotation finalRot = KinematicsToolkit.integrate(IntegrationType.WILCOX_1,
initOrientation, initDate, finalDate, spin, dt);
The order integer is the approximation order : the ones available are 1 to 4.
- Edwards method :
Rotation finalRot = KinematicsToolkit.integrate(IntegrationType.EDWARDS,
initOrientation, initDate, finalDate, spin, dt);
Differentiate and integrate a vector
In a similar way to the orientation function, a new class has been added in order to represent a time-dependent 3-D vector function. This class implements the Vector3DFunction interface, and it contains the methods to compute the derivative of the vector or its integral over a time period. The computation can be done using a numerical method or it can be analytical, when possible.
Compute the spin
The Kinematics package contains some methods aiming to compute the instantaneous spin. These methods are listed hereafter:
- Estimation: two rotations corresponding to two different dates are used to compute the spin (the velocity is supposed to be constant during the time interval between the two rotations).
This function is implemented by the following method in the kinematics toolkit:
public static Vector3D estimateSpin(final Rotation start, final Rotation end, final double dt)
.
- [math]\displaystyle{ \Omega_{S/R}^{[S]} = 2Q_{S/R}\dot{Q}_{S/R} }[/math], when knowing the derivative of the quaternion.
This equation is implemented by the following kinematics toolkit method:
public static Vector3D computeSpin(final Quaternion q, final Quaternion qd)
.
- Using the derivative of the Euler or Cardan angles:
- Euler (not to be used when the angles are small):
[math]\displaystyle{ \Omega_{S/R}^{[S]} = \left[ \begin{array}{c} \dot{\psi}\sin(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\sin(\theta)\cos(\phi)- \dot{\theta}\sin(\phi) \\ \dot{\psi}\cos(\theta) + \dot{\phi} \end{array} \right] }[/math]
- Cardan (only to be used when the angles are small):
[math]\displaystyle{ \Omega_{S/R}^{[S]} = \left[ \begin{array}{c}-\dot{\psi}\sin(\theta)+\dot{\phi} \\ \dot{\psi}\cos(\theta)\sin(\phi) + \dot{\theta}\cos(\phi) \\ \dot{\psi}\cos(\theta)\cos(\phi) - \dot{\theta}\sin(\phi) \end{array} \right] }[/math]
These formula are implemented by the following kinematics toolkit method:
public static Vector3D computeSpin(final double[] ang, final double[] angd, final RotationOrder order)
.
- Analytic computation: if the spin is represented by a function, its instantaneous value must be obtained by direct analytic computation (the
IVector3DFunctionclasses have been created for this purpose)
Getting Started
TBD
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| OrientationFunction | This interface represents a generic univariate orientation function. | ... |
| Vector3DFunction | This interface represents a generic univariate 3-D vector function. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| AbstractOrientationFunction | This class represents an orientation function. | ... |
| AbstractVector3DFunction | This class represents a spin function, or a spin n-th derivative function. | ... |
Tutorials
Tutorial 1
Modèle:SpecialInclusion prefix=$theme sub section="Tuto1"/
Tutorial 2
Modèle:SpecialInclusion prefix=$theme sub section="Tuto2"/