« User Manual 3.3 Root-Finding Algorithms » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| (5 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 99 : | Ligne 99 : | ||
The library defines the following interfaces related to solvers: | The library defines the following interfaces related to solvers: | ||
|=Interface|= | {| class="wikitable" | ||
|'''UnivariateSolver'''|Interface for a univariate solver|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/UnivariateSolver.html ...] | |- | ||
|''' | ! scope="col"| Interface | ||
! scope="col"| Summary | |||
! scope="col"| Javadoc | |||
|- | |||
|'''UnivariateSolver''' | |||
|Interface for a univariate solver | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/UnivariateSolver.html ...] | |||
|- | |||
|'''UnivariateDifferentiableSolver''' | |||
|Interface for a differentiable univariate real solver | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/DifferentiableUnivariateSolver.html ...] | |||
|} | |||
=== Classes === | === Classes === | ||
This section is about the following classes related to solvers : | This section is about the following classes related to solvers : | ||
|=Class|= | {| class="wikitable" | ||
|'''BrentSolver'''|Brent solver implementation.|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/BrentSolver.html ...] | |- | ||
|''' | ! scope="col"| Class | ||
|'''BisectionSolver'''|Bisection solver implementation.|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/BisectionSolver.html ...] | ! scope="col"| Summary | ||
|'''MullerSolver'''|Müller solver implementation.|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/MullerSolver.html ...] | ! scope="col"| Javadoc | ||
|- | |||
|'''BrentSolver''' | |||
|Brent solver implementation. | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/BrentSolver.html ...] | |||
|- | |||
|'''NewtonRaphsonSolver''' | |||
|Newton-Raphson solver implementation. | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/NewtonSolver.html ...] | |||
|- | |||
|'''BisectionSolver''' | |||
|Bisection solver implementation. | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/BisectionSolver.html ...] | |||
|- | |||
|'''MullerSolver''' | |||
|Müller solver implementation. | |||
|[{{JavaDoc3.3}}/org/apache/commons/math3/analysis/solvers/MullerSolver.html ...] | |||
|} | |||
=== Brent method === | === Brent method === | ||
The'''''Brent's method''''' is a root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods. The idea is to use the secant method or inverse quadratic interpolation if possible, because they converge faster, but to fall back to the more robust bisection method if necessary. | The '''''Brent's method''''' is a root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods. The idea is to use the secant method or inverse quadratic interpolation if possible, because they converge faster, but to fall back to the more robust bisection method if necessary. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 169 : | Ligne 197 : | ||
=== Newton method === | === Newton method === | ||
The'''''Newton's method''''' (also known as the Newton–Raphson method) is a method for finding successively better approximations to the roots of a real-valued function. The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line, and one computes the x-intercept of this tangent line. This x-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated. | The '''''Newton's method''''' (also known as the Newton–Raphson method) is a method for finding successively better approximations to the roots of a real-valued function. The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line, and one computes the x-intercept of this tangent line. This x-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated. | ||
IMPORTANT : the Newton solver only works for differentiable functions, this is reflected in the interface and class inheritances. | IMPORTANT : the Newton solver only works for differentiable functions, this is reflected in the interface and class inheritances. | ||
| Ligne 217 : | Ligne 245 : | ||
=== Bisection method === | === Bisection method === | ||
The'''''bisection method''''' is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow. | The '''''bisection method''''' is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 243 : | Ligne 271 : | ||
=== Müller method === | === Müller method === | ||
The'''''Müller's method''''' is based on the secant method, which constructs at every iteration a line through two points on the graph of f. Instead, Müller's method uses three points, constructs the parabola through these three points, and takes the intersection of the x-axis with the parabola to be the next approximation. | The '''''Müller's method''''' is based on the secant method, which constructs at every iteration a line through two points on the graph of f. Instead, Müller's method uses three points, constructs the parabola through these three points, and takes the intersection of the x-axis with the parabola to be the next approximation. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 288 : | Ligne 316 : | ||
* read the solvers' javadoc carefully, | * read the solvers' javadoc carefully, | ||
* always check if the solvers' results are appropriate. | * always check if the solvers' results are appropriate. | ||
[[Category:User_Manual_3.3_Mathematics]] | |||
Dernière version du 27 février 2018 à 13:43
Introduction
Scope
This section is about the root-finding algorithms for univariate real functions provided by the library. First we explain how to use the root-finding algorithms. Then a focus is made on the following root finding methods: Brent, Newton, Bisection and Müller.
Javadoc
All solvers are in the following package : org.apache.commons.math3.analysis.solvers
Links
None as of now.
Useful Documents
None as of now.
Package Overview
The package org.apache.commons.math3.analysis.solvers contains all the solvers described here.
Features Description
About root finding
This library provides root-finding algorithms for real univariate functions, all coming from the commons-math library. The function for which a root is searched has to be provided as a UnivariateFunction. The root-finding algorithm is implemented through the UnivariateSolver interface.
A very generic example would be :
UnivariateFunction f = <some function>;
UnivariateSolver solver = <some solver>;
int numberOfEvals = 100;
double startInterval = 5.;
double endInterval = 10.;
double root = solver.solve(numberOfEvals , f, startInterval , endInterval);
This means the solver with look for a root value of f in the interval [5. , 10.], and will have to do so in no more than 100 evaluation steps.
Test functions
We will demonstrate the use of root-finding algorithms with two test input functions : a periodic function and a linear function. These functions are defined as follows : sinus function : SinFunction
public class SinFunction implements DifferentiableUnivariateFunction {
public double value(double x) {
return FastMath.sin(x);
}
public UnivariateFunction derivative() {
return new UnivariateFunction() {
public double value(double x) {
return FastMath.cos(x);
}
};
}
linear function : XMinus5Function
public class XMinus5Function implements DifferentiableUnivariateFunction {
public double value(double x) {
return x- 5;
}
public UnivariateFunction derivative() {
return new UnivariateFunction() {
public double value(double x) {
return 1.0;
}
};
}
Available solvers
The library provides around ten solvers, but the following have been more thoroughly tested :
- BrentSolver
- NewtonSolver
- BisectionSolver
- MullerSolver
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
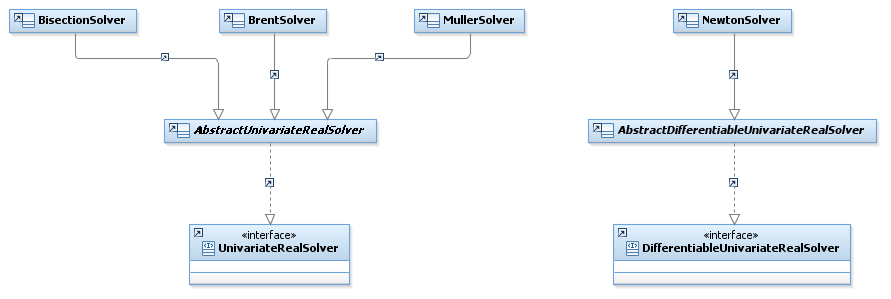
Interfaces
The library defines the following interfaces related to solvers:
| Interface | Summary | Javadoc |
|---|---|---|
| UnivariateSolver | Interface for a univariate solver | ... |
| UnivariateDifferentiableSolver | Interface for a differentiable univariate real solver | ... |
Classes
This section is about the following classes related to solvers :
| Class | Summary | Javadoc |
|---|---|---|
| BrentSolver | Brent solver implementation. | ... |
| NewtonRaphsonSolver | Newton-Raphson solver implementation. | ... |
| BisectionSolver | Bisection solver implementation. | ... |
| MullerSolver | Müller solver implementation. | ... |
Brent method
The Brent's method is a root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods. The idea is to use the secant method or inverse quadratic interpolation if possible, because they converge faster, but to fall back to the more robust bisection method if necessary.
UnivariateFunction f = new SinFunction ();
double r;
UnivariateSolver solver = new BrentSolver();
r = solver.solve(100, f, 3, 4);
Result : r = PI
UnivariateFunction f = new XMinus5Function ();
double r;
UnivariateSolver solver = new BrentSolver();
r = solver.solve(100, f, 1, 2);
Result : NoBracketingException exception
behavior deteriorated in case of several roots in the interval :
UnivariateFunction f = new SinFunction ();
double r;
UnivariateSolver solver = new BrentSolver();
r = solver.solve(100, f, 1, 20);
Result : r = PI
UnivariateFunction f = new SinFunction ();
double r;
UnivariateSolver solver = new BrentSolver();
r = solver.solve(100, f, 2, 20);
Result : r = 3 PI
UnivariateFunction f = new SinFunction ();
double r;
UnivariateSolver solver = new BrentSolver();
r = solver.solve(100, f, 7, 20);
Result : NoBracketingException exception
Newton method
The Newton's method (also known as the Newton–Raphson method) is a method for finding successively better approximations to the roots of a real-valued function. The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line, and one computes the x-intercept of this tangent line. This x-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated.
IMPORTANT : the Newton solver only works for differentiable functions, this is reflected in the interface and class inheritances.
DifferentiableUnivariateFunction f = new XMinus5Function ();
double r;
DifferentiableUnivariateSolver solver = new NewtonSolver();
r = solver.solve(100, f, 1, 6);
Result : r = 5
aberrant behavior :
DifferentiableUnivariateFunction f = new SinFunction();
double r;
DifferentiableUnivariateSolver solver = new NewtonSolver();
r = solver.solve(100, f, 1, 2);
Result : r =- 4 PI
DifferentiableUnivariateFunction f = new SinFunction();
double r;
DifferentiableUnivariateSolver solver = new NewtonSolver();
r = solver.solve(100, f, 1, 3);
Result : r = PI
DifferentiableUnivariateFunction f = new XMinus5Function ();
double r;
DifferentiableUnivariateSolver solver = new NewtonSolver();
r = solver.solve(100, f, 5.1, 20);
Result : r = 5
Bisection method
The bisection method is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow.
UnivariateFunction f = new XMinus5Function ();
double r;
UnivariateSolver solver = new BisectionSolver();
r = solver.solve(100, f, 3, 4);
Result : r = PI
behavior deteriorated :
UnivariateFunction f = new XMinus5Function ();
double r;
UnivariateSolver solver = new BisectionSolver();
r = solver.solve(100, f, 5.1, 20);
Result : r = 20 (the upper bound of the interval)
Müller method
The Müller's method is based on the secant method, which constructs at every iteration a line through two points on the graph of f. Instead, Müller's method uses three points, constructs the parabola through these three points, and takes the intersection of the x-axis with the parabola to be the next approximation.
UnivariateFunction f = new XMinus5Function ();
double r;
UnivariateSolver solver = new MullerSolver();
r = solver.solve(100, f, 1, 6);
Result : r = 5
UnivariateFunction f = new XMinus5Function ();
double r;
UnivariateSolver solver = new MullerSolver();
r = solver.solve(100, f, 2, 3);
Result : NoBracketingException exception
UnivariateFunction f = new SinFunction ();
double r;
UnivariateSolver solver = new MullerSolver();
r = solver.solve(100, f, 1, 20);
Result : NoBracketingException exception
Tutorials
Tutorial 1
Modèle:SpecialInclusion prefix=$theme sub section="Tuto1"/
Tutorial 2
Modèle:SpecialInclusion prefix=$theme sub section="Tuto2"/
 Tips & Tricks
Tips & Tricks
Summing up : the solvers appear to behave in unexpected ways when the initial conditions are not "ideal". Therefore It is advised, when using the solvers, to :
- avoid non-ideal initial conditions,
- read the solvers' javadoc carefully,
- always check if the solvers' results are appropriate.