User Manual 3.4.1 Spheroids : Différence entre versions
(Page créée avec « ==== Definition ==== A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellip... ») |
|||
| Ligne 3 : | Ligne 3 : | ||
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal equatorial radii. Assuming the XYZ coordinate system is such that the spheroid is centered and axis-aligned, the spheroids equation is given by: | A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal equatorial radii. Assuming the XYZ coordinate system is such that the spheroid is centered and axis-aligned, the spheroids equation is given by: | ||
| − | + | <center><math>\mathcal{S} = \left\{ (x, y, z) \in \mathbb{R}^3 \middle/ {x^2 + y^2 \over a^2} + {z^2 \over b^2} = 1\right\}</math></center> | |
| − | + | ||
| − | + | [[File:spheroid.PNG|center]] | |
| − | [[ | + | |
| − | The equatorial radius is called the transverse radius whereas the polar radius | + | The equatorial radius is called the transverse radius whereas the polar radius <math>b</math> is the conjugate radius. |
==== Implementation ==== | ==== Implementation ==== | ||
| − | The Spheroid object in the SIRIUS library implements the [ | + | The Spheroid object in the SIRIUS library implements the [MAT_GEO_EllipsoidInterface Ellipsoid interface]. Please refer to the [{{JavaDoc3.4.1}}/org/apache/commons/math3/geometry/euclidean/threed/Spheroid.html Javadoc] for a complete list of public methods. |
==== Instantiation ==== | ==== Instantiation ==== | ||
| − | In order to instantiate a spheroid object, the user must specify the spheroids' center, it's axis of revolution and both semi-axis (the transverse radius | + | In order to instantiate a spheroid object, the user must specify the spheroids' center, it's axis of revolution and both semi-axis (the transverse radius <math>a</math> and the conjugate radius <math>b</math>). For example : |
| − | + | <syntaxhighlight lang="java"> | |
// Spheroid parameters | // Spheroid parameters | ||
Vector3D position = new Vector3D(1, 2, 3); | Vector3D position = new Vector3D(1, 2, 3); | ||
| Ligne 27 : | Ligne 25 : | ||
// The spheroid itself | // The spheroid itself | ||
Spheroid mySpheroid = new Spheroid(position, revAxis, a, b); | Spheroid mySpheroid = new Spheroid(position, revAxis, a, b); | ||
| − | + | </syntaxhighlight> | |
==== Usage ==== | ==== Usage ==== | ||
| − | Please refer to the [ | + | Please refer to the [MAT_GEO_Home#HInteractions Interactions with other geometrical objects section] for methods inherited from the Shape interface. |
Version actuelle en date du 4 avril 2018 à 13:16
Definition
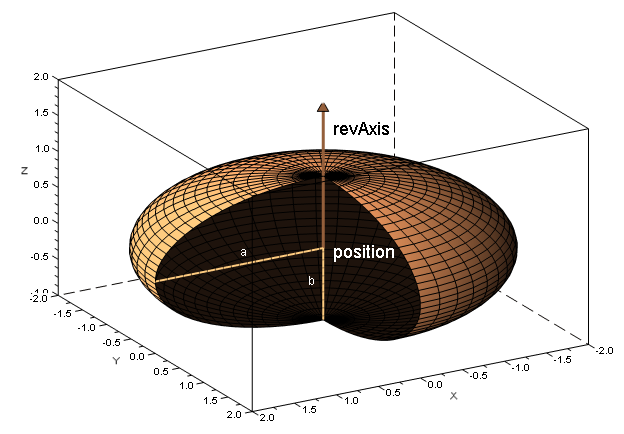
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal equatorial radii. Assuming the XYZ coordinate system is such that the spheroid is centered and axis-aligned, the spheroids equation is given by:
The equatorial radius is called the transverse radius whereas the polar radius [math]b[/math] is the conjugate radius.
Implementation
The Spheroid object in the SIRIUS library implements the [MAT_GEO_EllipsoidInterface Ellipsoid interface]. Please refer to the Javadoc for a complete list of public methods.
Instantiation
In order to instantiate a spheroid object, the user must specify the spheroids' center, it's axis of revolution and both semi-axis (the transverse radius [math]a[/math] and the conjugate radius [math]b[/math]). For example :
// Spheroid parameters Vector3D position = new Vector3D(1, 2, 3); Vector3D revAxis = new Vector3D(0, 1, 1); double a = 2.0; double b = 1.0; // The spheroid itself Spheroid mySpheroid = new Spheroid(position, revAxis, a, b);
Usage
Please refer to the [MAT_GEO_Home#HInteractions Interactions with other geometrical objects section] for methods inherited from the Shape interface.