« User Manual 4.0 Rotations and quaternions » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| (11 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
__NOTOC__ | |||
== Introduction == | == Introduction == | ||
=== Scope === | === Scope === | ||
| Ligne 7 : | Ligne 6 : | ||
=== Javadoc === | === Javadoc === | ||
The relevant packages are documented here : | The relevant packages are documented here : | ||
|=Library| | |||
| Patrius |[{{ | {| class="wikitable" | ||
| Patrius|[{{ | |- | ||
! scope="col"| Library | |||
! scope="col"| Javadoc | |||
|- | |||
| Patrius | |||
|[{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/package-summary.html Package fr.cnes.sirius.patrius.math.geometry.euclidean.threed] | |||
|- | |||
| Patrius | |||
|[{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/complex/package-summary.html Package fr.cnes.sirius.patrius.math.complex] | |||
|} | |||
=== Links === | === Links === | ||
| Ligne 29 : | Ligne 37 : | ||
== Features Description == | == Features Description == | ||
=== Rotations === | === Rotations === | ||
The Rotation is part of the math package fr.cnes.sirius.patrius.math | The Rotation is part of the math package fr.cnes.sirius.patrius.math.geometry.euclidean.threed. | ||
.geometry.euclidean.threed. | |||
The Rotation is represented by a [{{ | The Rotation is represented by a [{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/complex/Quaternion.html quaternion]: it is a unit quaternion (a quaternion of norm one).<br> | ||
The [{{ | The [{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Rotation.html Rotation class] represents an algebraic rotation (i.e. a mathematical rotation). | ||
In a three dimensional space, a rotation <math>r</math> is a function that maps vectors to vectors <math>r: \vec{v} \mapsto \vec{w}</math>. The rotation can be defined by one angle <math>\theta</math> and one axis <math>\vec{u}</math>, transforming <math>\vec{v}</math> into <math>\vec{w}</math> as described in the following figure. | In a three dimensional space, a rotation <math>r</math> is a function that maps vectors to vectors <math>r: \vec{v} \mapsto \vec{w}</math>. The rotation can be defined by one angle <math>\theta</math> and one axis <math>\vec{u}</math>, transforming <math>\vec{v}</math> into <math>\vec{w}</math> as described in the following figure. | ||
| Ligne 42 : | Ligne 49 : | ||
=== Quaternions === | === Quaternions === | ||
An advantageous way to deal with rotations is by using quaternions (class <code>Quaternion</code>). The quaternion that represents the rotation <math>r</math> defined by an angle <math>\theta</math> and a'''normalized''' axis <math>\vec{u}</math> is : | An advantageous way to deal with rotations is by using quaternions (class <code>Quaternion</code>). The quaternion that represents the rotation <math>r</math> defined by an angle <math>\theta</math> and a '''normalized''' axis <math>\vec{u}</math> is : | ||
<center> | |||
<math>Q = \left( \begin{array}{ccc} | <math>Q = \left( \begin{array}{ccc} | ||
cos(\theta / 2) \\ | cos(\theta / 2) \\ | ||
\vec{u}.sin(\theta / 2) \end{array} \right)</math> | \vec{u}.sin(\theta / 2) \end{array} \right)</math> | ||
</center> | |||
With <math>\vec{u} = ( u_x, u_y, u_z )</math>, <math>Q</math> can also be written as : | With <math>\vec{u} = ( u_x, u_y, u_z )</math>, <math>Q</math> can also be written as : | ||
<center> | |||
<math>Q = \left( \begin{array}{ccc} | <math>Q = \left( \begin{array}{ccc} | ||
cos(\theta / 2) \\ | cos(\theta / 2) \\ | ||
| Ligne 56 : | Ligne 64 : | ||
u_y.sin(\theta / 2) \\ | u_y.sin(\theta / 2) \\ | ||
u_z.sin(\theta / 2)\end{array} \right)</math> | u_z.sin(\theta / 2)\end{array} \right)</math> | ||
</center> | |||
Quaternions that represent rotations are normalized : | Quaternions that represent rotations are normalized : | ||
<math>||Q|| = q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1</math> | <center><math>||Q|| = q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1</math></center> | ||
For normalized quaternions, the inverse quaternion <math>Q^{-1}</math> is the same as the conjugate <math>Q^*</math>: | For normalized quaternions, the inverse quaternion <math>Q^{-1}</math> is the same as the conjugate <math>Q^*</math>: | ||
<center> | |||
<math>Q^{-1} =Q^* = \left( \begin{array}{ccc} | <math>Q^{-1} =Q^* = \left( \begin{array}{ccc} | ||
cos(\theta / 2) \\ | cos(\theta / 2) \\ | ||
-\vec{u}.sin(\theta / 2) \end{array} \right)</math> | -\vec{u}.sin(\theta / 2) \end{array} \right)</math> | ||
</center> | |||
The image <math>\vec{w}</math> of a vector <math>\vec{v}</math> transformed by the rotation represented by <math>Q</math> is given by : | The image <math>\vec{w}</math> of a vector <math>\vec{v}</math> transformed by the rotation represented by <math>Q</math> is given by : | ||
<math>\vec{w} = Q.\vec{v}.Q^{*}</math> | <center><math>\vec{w} = Q.\vec{v}.Q^{*}</math></center> | ||
====Examples of rotations and associated quaternions==== | ====Examples of rotations and associated quaternions==== | ||
The rotation defined by the angle <math>\theta = \pi/2</math> and the axis <math>\vec{u} = \vec{z}</math> is represented by the quaternion : | The rotation defined by the angle <math>\theta = \pi/2</math> and the axis <math>\vec{u} = \vec{z}</math> is represented by the quaternion : | ||
<center> | |||
<math>Q = \left( \begin{array}{ccc} | <math>Q = \left( \begin{array}{ccc} | ||
cos(\pi / 4) \\ | cos(\pi / 4) \\ | ||
| Ligne 83 : | Ligne 94 : | ||
0 \\ | 0 \\ | ||
\sqrt 2 / 2\end{array} \right)</math> | \sqrt 2 / 2\end{array} \right)</math> | ||
</center> | |||
The rotation defined by the angle <math>\theta = 2\pi/3</math> and the axis <math>\vec{u} = (1,1,1)</math> (witch has to be normalized) is represented by the quaternion : | The rotation defined by the angle <math>\theta = 2\pi/3</math> and the axis <math>\vec{u} = (1,1,1)</math> (witch has to be normalized) is represented by the quaternion : | ||
<center> | |||
<math>Q = \left( \begin{array}{ccc} | <math>Q = \left( \begin{array}{ccc} | ||
cos(\pi / 3) \\ | cos(\pi / 3) \\ | ||
| Ligne 95 : | Ligne 108 : | ||
1 / 2 \\ | 1 / 2 \\ | ||
1 / 2\end{array} \right)</math> | 1 / 2\end{array} \right)</math> | ||
</center> | |||
====Rotation composition with quaternions==== | ====Rotation composition with quaternions==== | ||
<math>r_1: \vec{w_1} \mapsto \vec{w_2}</math> and <math>r_2: \vec{w_2} \mapsto \vec{w_3}</math> being two known rotations, the rotation composition <math>r: \vec{w_1} \mapsto \vec{w_3}</math> can be computed as well. The quaternion corresponding to that new rotation is: | <math>r_1: \vec{w_1} \mapsto \vec{w_2}</math> and <math>r_2: \vec{w_2} \mapsto \vec{w_3}</math> being two known rotations, the rotation composition <math>r: \vec{w_1} \mapsto \vec{w_3}</math> can be computed as well. The quaternion corresponding to that new rotation is: | ||
<math>Q = Q{_2}.Q{_1}</math>. | <center><math>Q = Q{_2}.Q{_1}</math>.</center> | ||
This can be proven as follows: | This can be proven as follows: | ||
| Ligne 107 : | Ligne 121 : | ||
Substituting <math>\vec{w_2}</math> in the expression of <math>\vec{w_3}</math>: | Substituting <math>\vec{w_2}</math> in the expression of <math>\vec{w_3}</math>: | ||
<math>\vec{w_3} = Q{_2}.Q{_1}.\vec{w_1} .Q_{1}^{-1}.Q_{2}^{-1} = (Q{_2}.Q{_1}).\vec{w_1} .(Q_{2}.Q_{1})^{-1} = Q.\vec{w_1} .Q^{-1}</math>. | <center><math>\vec{w_3} = Q{_2}.Q{_1}.\vec{w_1} .Q_{1}^{-1}.Q_{2}^{-1} = (Q{_2}.Q{_1}).\vec{w_1} .(Q_{2}.Q_{1})^{-1} = Q.\vec{w_1} .Q^{-1}</math>.</center> | ||
Notice that in the expression of the quaternion <math>Q</math> the rightmost quaternion is the one corresponding to the first rotation to be performed. | Notice that in the expression of the quaternion <math>Q</math> the rightmost quaternion is the one corresponding to the first rotation to be performed. | ||
| Ligne 114 : | Ligne 128 : | ||
=== Rotation matrices === | === Rotation matrices === | ||
The matrix representation of a rotation is very intuitive altough more redundant compared to quaternions. A rotation matrix is a 3x3 (real) square matrix. | The matrix representation of a rotation is very intuitive altough more redundant compared to quaternions. A rotation matrix is a 3x3 (real) square matrix.<br> | ||
If the rotation <math>r</math> transforms an inital basis <math>(\vec{x}, \vec{y}, \vec{z})</math> to a new one <math>(\vec{i}, \vec{j}, \vec{k})</math> the columns of the rotation matrix are given by the components of the rotated basis vectors, expressed in the initial one. | If the rotation <math>r</math> transforms an inital basis <math>(\vec{x}, \vec{y}, \vec{z})</math> to a new one <math>(\vec{i}, \vec{j}, \vec{k})</math> the columns of the rotation matrix are given by the components of the rotated basis vectors, expressed in the initial one. | ||
<math>M = \left( \begin{array}{ccc} | <center><math>M = \left( \begin{array}{ccc} | ||
i_x & j_x & k_x \\ | i_x & j_x & k_x \\ | ||
i_y & j_y & k_y \\ | i_y & j_y & k_y \\ | ||
i_z & j_z & k_z \end{array} \right)</math> | i_z & j_z & k_z \end{array} \right)</math> | ||
</center> | |||
The matrix <math>M</math> has the following properties: | The matrix <math>M</math> has the following properties: | ||
| Ligne 132 : | Ligne 146 : | ||
Given a quaternion <math>Q = ( q_0, q_1, q_2, q_3 )</math> the rotation matrix has the following expression in term of the components of <math>Q</math>: | Given a quaternion <math>Q = ( q_0, q_1, q_2, q_3 )</math> the rotation matrix has the following expression in term of the components of <math>Q</math>: | ||
<center> | |||
<math>M = \left( \begin{array}{ccc} | <math>M = \left( \begin{array}{ccc} | ||
q_0^2 + q_1^2-q_2^2 -q_3^2 & 2q_1q_2 + q_0q_3 & 2q_0q_2 + q_1q_3 \\ | q_0^2 + q_1^2-q_2^2 -q_3^2 & 2q_1q_2 + q_0q_3 & 2q_0q_2 + q_1q_3 \\ | ||
2q_0q_3 + q_1q_2 & q_0^2 + q_1^2-q_2^2 -q_3^2 & 2q_2q_3 + q_0q_1 \\ | 2q_0q_3 + q_1q_2 & q_0^2 + q_1^2-q_2^2 -q_3^2 & 2q_2q_3 + q_0q_1 \\ | ||
2q_1q_3 + q_0q_2 & 2q_0q_1 + q_2q_3 & q_0^2 + q_1^2-q_2^2 -q_3^2 \end{array} \right)</math> | 2q_1q_3 + q_0q_2 & 2q_0q_1 + q_2q_3 & q_0^2 + q_1^2-q_2^2 -q_3^2 \end{array} \right)</math></center> | ||
=== Rotation interpolation === | === Rotation interpolation === | ||
There are two implemented rotations interpolation methods : | There are two implemented rotations interpolation methods : | ||
- LERP | - LERP<br> | ||
- SLERP | - SLERP | ||
=== LERP === | === LERP === | ||
The LERP (linear interpolation method) is a method of curve fitting using linear polynomials. It is used for rotation interpolation goal in the PATRIUS library and relies on quaternion properties. | The LERP (linear interpolation method) is a method of curve fitting using linear polynomials. It is used for rotation interpolation goal in the PATRIUS library and relies on quaternion properties.<br> | ||
Let <math>q_{0}</math> and <math>q_{1}</math> be two normed quaternions and <math>t</math> an interpolation parameter in the [0;1] range. We can defined <math>q_{t}</math> as the interpolated quaternion so as: | Let <math>q_{0}</math> and <math>q_{1}</math> be two normed quaternions and <math>t</math> an interpolation parameter in the [0;1] range. We can defined <math>q_{t}</math> as the interpolated quaternion so as: | ||
| Ligne 180 : | Ligne 194 : | ||
=== Building Rotations === | === Building Rotations === | ||
Rotations can be represented by several different mathematical entities (matrices, axis and angle, Cardan or Euler angles, quaternions). The user can build a rotation from any of these representations, and any of these representations can be retrieved from a [{{ | Rotations can be represented by several different mathematical entities (matrices, axis and angle, Cardan or Euler angles, quaternions). The user can build a rotation from any of these representations, and any of these representations can be retrieved from a [{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Rotation.html Rotation instance]. | ||
In addition, a rotation can also be built implicitly from a set of vectors and their image or just a vector and its image. | In addition, a rotation can also be built implicitly from a set of vectors and their image or just a vector and its image. | ||
| Ligne 187 : | Ligne 201 : | ||
The rotation can be built from a rotation quaternion using one of the following constructors : | The rotation can be built from a rotation quaternion using one of the following constructors : | ||
* | *'''''Rotation(boolean needsNormalization, double q0, double q1, double q2, double q3)''''' | ||
''' | *'''''Rotation(boolean needsNormalization, final Quaternion quaternion)''''' | ||
* | *'''''Rotation(boolean needsNormalization, final double[] q)''''' | ||
A rotation can be built from a normalized quaternion, i.e. a quaternion for which <math>q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1</math>. If the quaternion is not normalized, the constructor can normalize it in a preprocessing step. | A rotation can be built from a normalized quaternion, i.e. a quaternion for which <math>q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1</math>. If the quaternion is not normalized, the constructor can normalize it in a preprocessing step. | ||
| Ligne 195 : | Ligne 209 : | ||
Note that some conventions put the scalar part of the quaternion as the fourth component and the vector part as the first three components. The scalar part is put as the first component. | Note that some conventions put the scalar part of the quaternion as the fourth component and the vector part as the first three components. The scalar part is put as the first component. | ||
The rotation quaternion can be retrieve using '''''getQuaternion()''''' or '''''getQi()'''''. | |||
==== Axis-angle representation ==== | ==== Axis-angle representation ==== | ||
| Ligne 210 : | Ligne 224 : | ||
If necessary, the quaternion is normalized. | If necessary, the quaternion is normalized. | ||
The axis and the angle can be retrieved using '''''getAxis()''''' and '''''getAngle()'''''. | |||
==== Matrix representation ==== | ==== Matrix representation ==== | ||
The rotation can be built from a rotation matrix with the following constructor : | The rotation can be built from a rotation matrix with the following constructor : | ||
*'''''Rotation(double[][] m, double threshold)''''' | |||
The rotation matrix can be retrieved using'''''getMatrix()'''''. | The rotation matrix can be retrieved using '''''getMatrix()'''''. | ||
==== Euler Angles ==== | ==== Euler Angles ==== | ||
| Ligne 239 : | Ligne 253 : | ||
==== Others representations ==== | ==== Others representations ==== | ||
See [{{ | See [{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Rotation.html Rotation javadoc]. | ||
=== Using Rotations === | === Using Rotations === | ||
| Ligne 245 : | Ligne 259 : | ||
.geometry.euclidean.threed. | .geometry.euclidean.threed. | ||
The Rotation is represented by a rotation quaternion : it is a unit quaternion (a quaternion of norm one). | The Rotation is represented by a rotation quaternion : it is a unit quaternion (a quaternion of norm one).<br> | ||
The [{{ | The [{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Rotation.html Rotation class] represents an algebraic rotation (i.e. a mathematical rotation). | ||
==== Rotate a vector ==== | ==== Rotate a vector ==== | ||
A rotation is an operator which basically rotates three dimensional [{{ | A rotation is an operator which basically rotates three dimensional [{{JavaDoc4.1}}//fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Vector3D.html vectors] into other three dimensional [{{JavaDoc4.1}}//fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Vector3D.html vectors] using '''''applyTo()'''''. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 267 : | Ligne 281 : | ||
Since a rotation is basically a vectorial operator, several rotations can be composed together and the composite operation r = r2 o r1 is also a rotation. r1 is applied before r2 and the operator'''''applyTo()''''' is used. | Since a rotation is basically a vectorial operator, several rotations can be composed together and the composite operation r = r2 o r1 is also a rotation. r1 is applied before r2 and the operator '''''applyTo()''''' is used. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 286 : | Ligne 300 : | ||
==== Change the basis of a vector ==== | ==== Change the basis of a vector ==== | ||
The rotation could be used to change the basis of a vector using'''''applyInverseTo()'''''. | The rotation could be used to change the basis of a vector using '''''applyInverseTo()'''''. | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 370 : | Ligne 384 : | ||
Same example given in Scilab using Celestlab macros library: | Same example given in Scilab using Celestlab macros library: | ||
<syntaxhighlight lang="scilab"> | |||
alpha1 = CL_deg2rad(30.); | alpha1 = CL_deg2rad(30.); | ||
q1 = CL_rot_axAng2quat([1;1;1],alpha1); | q1 = CL_rot_axAng2quat([1;1;1],alpha1); | ||
| Ligne 378 : | Ligne 392 : | ||
q = (1/norm(q))* q | q = (1/norm(q))* q | ||
[axis, angle] = CL_rot_quat2axAng(q) | [axis, angle] = CL_rot_quat2axAng(q) | ||
</syntaxhighlight> | |||
==== SLERP Use example ==== | ==== SLERP Use example ==== | ||
| Ligne 401 : | Ligne 415 : | ||
Same example given in Scilab using Celestlab macros library: | Same example given in Scilab using Celestlab macros library: | ||
<syntaxhighlight lang="scilab"> | |||
alpha1 = CL_deg2rad(30.); | alpha1 = CL_deg2rad(30.); | ||
q1 = CL_rot_axAng2quat([1;1;1],alpha1); | q1 = CL_rot_axAng2quat([1;1;1],alpha1); | ||
| Ligne 409 : | Ligne 423 : | ||
[axis, angle] = CL_rot_quat2axAng(q) | [axis, angle] = CL_rot_quat2axAng(q) | ||
</syntaxhighlight> | |||
== Contents == | == Contents == | ||
| Ligne 418 : | Ligne 432 : | ||
The relevant classes are : | The relevant classes are : | ||
|=Class|= | {| class="wikitable" | ||
|'''Quaternion'''|This class implements quaternions.|[{{ | |- | ||
|'''Rotation'''|This class implements rotations in a three-dimensional space.|[{{ | ! scope="col"| Class | ||
|'''RotationOrder'''|This class is a utility representing a rotation order specification for Cardan or Euler angles specification.|[{{ | ! scope="col"| Summary | ||
! scope="col"| Javadoc | |||
|- | |||
|'''Quaternion''' | |||
|This class implements quaternions. | |||
|[{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/complex/Quaternion.html ...] | |||
|- | |||
|'''Rotation''' | |||
|This class implements rotations in a three-dimensional space. | |||
|[{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/Rotation.html ...] | |||
|- | |||
|'''RotationOrder''' | |||
|This class is a utility representing a rotation order specification for Cardan or Euler angles specification. | |||
|[{{JavaDoc4.1}}/fr/cnes/sirius/patrius/math/geometry/euclidean/threed/RotationOrder.html ...] | |||
|} | |||
[[Category:User_Manual_4.1_Mathematics]] | |||
Dernière version du 28 juin 2018 à 12:18
Introduction
Scope
This section describes rotation and quaternions.
Javadoc
The relevant packages are documented here :
| Library | Javadoc |
|---|---|
| Patrius | Package fr.cnes.sirius.patrius.math.geometry.euclidean.threed |
| Patrius | Package fr.cnes.sirius.patrius.math.complex |
Links
Useful Documents
None as of now.
Package Overview
The relevant functionality can be found in the following packages :
fr.cnes.sirius.patrius.math.complexfor the Quaternion class.fr.cnes.sirius.patrius.math.cnesmerge.geometry.euclidean.threedfor the Rotation class.fr.cnes.sirius.patrius.math.geometry.euclidean.threedfor the RotationOrder class.
Features Description
Rotations
The Rotation is part of the math package fr.cnes.sirius.patrius.math.geometry.euclidean.threed.
The Rotation is represented by a quaternion: it is a unit quaternion (a quaternion of norm one).
The Rotation class represents an algebraic rotation (i.e. a mathematical rotation).
In a three dimensional space, a rotation [math]\displaystyle{ r }[/math] is a function that maps vectors to vectors [math]\displaystyle{ r: \vec{v} \mapsto \vec{w} }[/math]. The rotation can be defined by one angle [math]\displaystyle{ \theta }[/math] and one axis [math]\displaystyle{ \vec{u} }[/math], transforming [math]\displaystyle{ \vec{v} }[/math] into [math]\displaystyle{ \vec{w} }[/math] as described in the following figure.
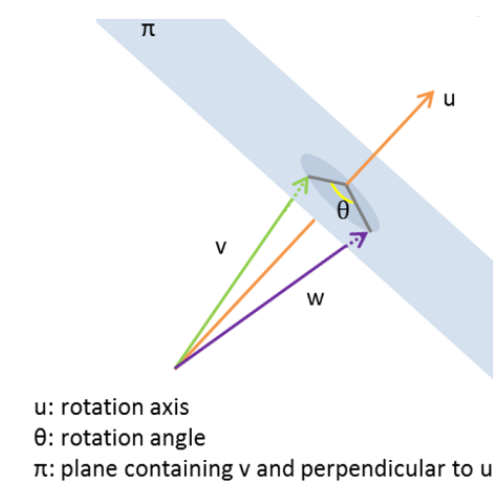
There are several ways to represent rotations. Amongst the most used are quaternions and rotation matrices. The following paragraphs aim to discuss each of them.
Quaternions
An advantageous way to deal with rotations is by using quaternions (class Quaternion). The quaternion that represents the rotation [math]\displaystyle{ r }[/math] defined by an angle [math]\displaystyle{ \theta }[/math] and a normalized axis [math]\displaystyle{ \vec{u} }[/math] is :
[math]\displaystyle{ Q = \left( \begin{array}{ccc} cos(\theta / 2) \\ \vec{u}.sin(\theta / 2) \end{array} \right) }[/math]
With [math]\displaystyle{ \vec{u} = ( u_x, u_y, u_z ) }[/math], [math]\displaystyle{ Q }[/math] can also be written as :
[math]\displaystyle{ Q = \left( \begin{array}{ccc} cos(\theta / 2) \\ u_x.sin(\theta / 2) \\ u_y.sin(\theta / 2) \\ u_z.sin(\theta / 2)\end{array} \right) }[/math]
Quaternions that represent rotations are normalized :
For normalized quaternions, the inverse quaternion [math]\displaystyle{ Q^{-1} }[/math] is the same as the conjugate [math]\displaystyle{ Q^* }[/math]:
[math]\displaystyle{ Q^{-1} =Q^* = \left( \begin{array}{ccc} cos(\theta / 2) \\ -\vec{u}.sin(\theta / 2) \end{array} \right) }[/math]
The image [math]\displaystyle{ \vec{w} }[/math] of a vector [math]\displaystyle{ \vec{v} }[/math] transformed by the rotation represented by [math]\displaystyle{ Q }[/math] is given by :
Examples of rotations and associated quaternions
The rotation defined by the angle [math]\displaystyle{ \theta = \pi/2 }[/math] and the axis [math]\displaystyle{ \vec{u} = \vec{z} }[/math] is represented by the quaternion :
[math]\displaystyle{ Q = \left( \begin{array}{ccc} cos(\pi / 4) \\ 0.sin(\pi / 4) \\ 0.sin(\pi / 4) \\ 1.sin(\pi / 4)\end{array} \right) = \left( \begin{array}{ccc} \sqrt 2 / 2 \\ 0 \\ 0 \\ \sqrt 2 / 2\end{array} \right) }[/math]
The rotation defined by the angle [math]\displaystyle{ \theta = 2\pi/3 }[/math] and the axis [math]\displaystyle{ \vec{u} = (1,1,1) }[/math] (witch has to be normalized) is represented by the quaternion :
[math]\displaystyle{ Q = \left( \begin{array}{ccc} cos(\pi / 3) \\ 1/\sqrt 3.sin(\pi / 3) \\ 1/\sqrt 3.sin(\pi / 3) \\ 1/\sqrt 3.sin(\pi / 3)\end{array} \right) = \left( \begin{array}{ccc} 1 / 2 \\ 1 / 2 \\ 1 / 2 \\ 1 / 2\end{array} \right) }[/math]
Rotation composition with quaternions
[math]\displaystyle{ r_1: \vec{w_1} \mapsto \vec{w_2} }[/math] and [math]\displaystyle{ r_2: \vec{w_2} \mapsto \vec{w_3} }[/math] being two known rotations, the rotation composition [math]\displaystyle{ r: \vec{w_1} \mapsto \vec{w_3} }[/math] can be computed as well. The quaternion corresponding to that new rotation is:
This can be proven as follows:
[math]\displaystyle{ \vec{w_2} = Q{_1}.\vec{w_1} .Q_{1}^{-1} }[/math] [math]\displaystyle{ \vec{w_3} = Q{_2}.\vec{w_2} .Q_{2}^{-1} }[/math]
Substituting [math]\displaystyle{ \vec{w_2} }[/math] in the expression of [math]\displaystyle{ \vec{w_3} }[/math]:
Notice that in the expression of the quaternion [math]\displaystyle{ Q }[/math] the rightmost quaternion is the one corresponding to the first rotation to be performed.
Rotation matrices
The matrix representation of a rotation is very intuitive altough more redundant compared to quaternions. A rotation matrix is a 3x3 (real) square matrix.
If the rotation [math]\displaystyle{ r }[/math] transforms an inital basis [math]\displaystyle{ (\vec{x}, \vec{y}, \vec{z}) }[/math] to a new one [math]\displaystyle{ (\vec{i}, \vec{j}, \vec{k}) }[/math] the columns of the rotation matrix are given by the components of the rotated basis vectors, expressed in the initial one.
The matrix [math]\displaystyle{ M }[/math] has the following properties:
- [math]\displaystyle{ M }[/math] is orthogonal (each column has norm 1)
- [math]\displaystyle{ det(M) = 1 }[/math]
- [math]\displaystyle{ M^{-1} = M^{T} }[/math]
Rotation matrix in term of quaternions
Given a quaternion [math]\displaystyle{ Q = ( q_0, q_1, q_2, q_3 ) }[/math] the rotation matrix has the following expression in term of the components of [math]\displaystyle{ Q }[/math]:
Rotation interpolation
There are two implemented rotations interpolation methods :
- LERP
- SLERP
LERP
The LERP (linear interpolation method) is a method of curve fitting using linear polynomials. It is used for rotation interpolation goal in the PATRIUS library and relies on quaternion properties.
Let [math]\displaystyle{ q_{0} }[/math] and [math]\displaystyle{ q_{1} }[/math] be two normed quaternions and [math]\displaystyle{ t }[/math] an interpolation parameter in the [0;1] range. We can defined [math]\displaystyle{ q_{t} }[/math] as the interpolated quaternion so as:
[math]\displaystyle{ q_{t}= q_{0} + t\times(q_{1}- q_{0}) }[/math]
SLERP
The SLERP (spherical linear interpolation method) refers to constant-speed motion along a unit-radius great circle arc, given the ends and an interpolation parameter between 0 and 1.It is used for rotation interpolation goal in the PATRIUS library. It relies on quaternion capabilities. Let [math]\displaystyle{ q_{0} }[/math] and [math]\displaystyle{ q_{1} }[/math] be two normed quaternions and [math]\displaystyle{ t }[/math] an interpolation parameter in the [0;1] range.
First method:
We can defined [math]\displaystyle{ q_{t} }[/math] as the interpolated quaternion so as :
[math]\displaystyle{ q_{t} = q_{0} ( q_{0}^{-1} q_{1} )' }[/math]
where-prime- operation is defined such as : [math]\displaystyle{ t, q(\theta, \vec{u}): q’ = q(t \times \theta, \vec{u}) }[/math]
Second method:
Another approch is to compute qt so as:
[math]\displaystyle{ q_{t} = q_{0} \frac{\sin (1-t)\lambda}{\sin \lambda} + q_{1} \frac{\sin (t \lambda)}{\sin \lambda} }[/math]
with lambda defined so as:
[math]\displaystyle{ \cos \lambda = q_{0} . q_{1} }[/math]
This latest approach saves computing time when dealing with many SLERP computing.
Getting Started
Building Rotations
Rotations can be represented by several different mathematical entities (matrices, axis and angle, Cardan or Euler angles, quaternions). The user can build a rotation from any of these representations, and any of these representations can be retrieved from a Rotation instance. In addition, a rotation can also be built implicitly from a set of vectors and their image or just a vector and its image.
Rotation quaternion
The rotation can be built from a rotation quaternion using one of the following constructors :
- Rotation(boolean needsNormalization, double q0, double q1, double q2, double q3)
- Rotation(boolean needsNormalization, final Quaternion quaternion)
- Rotation(boolean needsNormalization, final double[] q)
A rotation can be built from a normalized quaternion, i.e. a quaternion for which [math]\displaystyle{ q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1 }[/math]. If the quaternion is not normalized, the constructor can normalize it in a preprocessing step.
Note that some conventions put the scalar part of the quaternion as the fourth component and the vector part as the first three components. The scalar part is put as the first component.
The rotation quaternion can be retrieve using getQuaternion() or getQi().
Axis-angle representation
The rotation can be built from an axis [math]\displaystyle{ (x, y, z) }[/math] and an angle [math]\displaystyle{ \theta }[/math] with the following constructor :
// 90 deg rotation around z-axis
Vector3D axis = new Vector3D(0, 0, 1);
double angle = FastMath.PI / 2.;
Rotation r = new Rotation(axis, angle);
If necessary, the quaternion is normalized.
The axis and the angle can be retrieved using getAxis() and getAngle().
Matrix representation
The rotation can be built from a rotation matrix with the following constructor :
- Rotation(double[][] m, double threshold)
The rotation matrix can be retrieved using getMatrix().
Euler Angles
The RotationOrder class
The RotationOrder class contains static attributes, themselves being RotationOrder objects, describing every vector sequence that can be used to create a Rotation using Euler or Cardan angles.
Using Euler angles in rotations
A Rotation object can so be created using three angles and a RotationOrder describing the associated sequence of basis vectors. The user can also get the Cardan or Euler angles by giving a sequence, using the getAngles(RotationOrder) method. In some cases, there are singularities that make a rotation impossible to describe with a giver rotation order.
Code example :
Rotation rotation = new Rotation(RotationOrder.YZX, 0.12, 0.54, 0.45);
double[] angles = rotation.getAngles(RotationOrder.ZXY);
Others representations
See Rotation javadoc.
Using Rotations
The Rotation is part of the package fr.cnes.sirius.patrius.math .geometry.euclidean.threed.
The Rotation is represented by a rotation quaternion : it is a unit quaternion (a quaternion of norm one).
The Rotation class represents an algebraic rotation (i.e. a mathematical rotation).
Rotate a vector
A rotation is an operator which basically rotates three dimensional vectors into other three dimensional vectors using applyTo().
// vector A
Vector3D a = new Vector3D(1, 0, 0);
// build rotation r1
Vector3D u1 = new Vector3D(0, 0, 1);
double theta1 = FastMath.PI / 2. ;
Rotation r1 = new Rotation(u1, theta1);
// vector B, image of A by r1
Vector3D b = r1.applyTo(a);
Compose rotations
Since a rotation is basically a vectorial operator, several rotations can be composed together and the composite operation r = r2 o r1 is also a rotation. r1 is applied before r2 and the operator applyTo() is used.
// build rotation r1
Vector3D u1 = new Vector3D(0, 0, 1);
double theta1 = FastMath.PI / 2. ;
Rotation r1 = new Rotation(u1, theta1);
// build rotation r2
Vector3D u2 = new Vector3D(1, 0, 0);
double theta2 = FastMath.PI / 2. ;
Rotation r2 = new Rotation(u2, theta2);
// build r2 o r1
Rotation r2_o_r1 = r2.applyTo(r1);
// vector D, image of A by r2 o r1
Vector3D d = r2_o_r1.applyTo(a);
Change the basis of a vector
The rotation could be used to change the basis of a vector using applyInverseTo().
// Define frame R2 by building the rotation r12 in frame R1
Vector3D u12_R1 = new Vector3D(1, 1, 1);
double theta12 = FastMath.PI* 3. / 2.;
Rotation r12_R1 = new Rotation(u12_R1, theta12);
// vector A, expressed in R1
Vector3D a_R1 = new Vector3D(0.5, 0.5, 0);
// vector A, expressed in R2
Vector3D a_R2 = r12_R1.applyInverseTo(a_R1);
// Build rotation r, in R1 frame
Vector3D u_R1 = new Vector3D(0, 0, 1);
double theta = FastMath.PI;
Rotation r_R1 = new Rotation(u_R1, theta);
// Vector B, image of A by the rotation r, expressed in R1
Vector3D b_R1 = r_R1.applyTo(a_R1);
// Vector B, changed of basis, expressed in R2
Vector3D b_R2 = r12_R1.applyInverseTo(b_R1);
Change the basis of a rotation
Let be r a rotation built from the coordinates of its rotation axis. This vector is expressed in a frame [math]\displaystyle{ R_1 }[/math] ; the rotation is supported only in this frame. Let be [math]\displaystyle{ r_12 }[/math] the rotation from [math]\displaystyle{ R_1 }[/math] to [math]\displaystyle{ R_2 }[/math], i.e. the image of the axis [math]\displaystyle{ x_1 }[/math] expressed in [math]\displaystyle{ R_1 }[/math] using the rotation [math]\displaystyle{ r_12 }[/math] is the axis [math]\displaystyle{ x_2 }[/math] expressed in [math]\displaystyle{ R_2 }[/math] : [math]\displaystyle{ r_12(x_1) = x_2 }[/math] with [math]\displaystyle{ x_1 }[/math], [math]\displaystyle{ x_2 }[/math] and [math]\displaystyle{ r_12 }[/math] expressed in [math]\displaystyle{ R_1 }[/math].
The rotation r, changed of basis to be expressed in [math]\displaystyle{ R_2 }[/math] is obtained by[math]\displaystyle{ r_12 }[/math].applyTo(r.revert()).
// Define frame R2 by building the rotation r12 in frame R1
Vector3D u12_R1 = new Vector3D(1, 1, 1);
double theta12 = FastMath.PI* 3. / 2.;
Rotation r12_R1 = new Rotation(u12_R1, theta12);
// Build rotation r, in R1 frame
Vector3D u_R1 = new Vector3D(0, 0, 1);
double theta = FastMath.PI;
Rotation r_R1 = new Rotation(u_R1, theta);
// Change the basis of r
Rotation r_R2 = r12_R1.applyTo(r_R1.revert());
Using Quaternions
The Quaternion class provides all elementary operations on quaternions: sum, product, inverse, conjugate, norm, dot product, etc.
Below are some examples of use:
- Computing the product of two quaternions:
Quaternion qA = new Quaternion(qA0,qA1,qA2,qA3);
Quaternion qB = new Quaternion(qB0,qB1,qB2,qB3);
Quaternion qProduct = Quaternion.multiply(qA,qB);
- Getting the inverse of a quaternion :
Quaternion q = new Quaternion(0,5.1,4,8);
Quaternion qInverse = q.getInverse();
Using Rotations interpolation
LERP Use case
Here is an exemple on how one can compute LERP in Java language using PATRIUS:
final Vector3D axis = new Vector3D(1,1,1);
final Rotation r1 = new Rotation(axis,FastMath.PI/6.);
final Rotation r2 = new Rotation(axis,FastMath.PI/3.);
final Rotation r = Rotation.lerp(r1, r2, 0.5);
then one can retrieve corresponding rotation angle and axis:
final double rangle = r.getAngle();
final Vector3D raxis = r.getAxis();
Same example given in Scilab using Celestlab macros library:
alpha1 = CL_deg2rad(30.);
q1 = CL_rot_axAng2quat([1;1;1],alpha1);
alpha2 = CL_deg2rad(60.);
q2 = CL_rot_axAng2quat([1;1;1],alpha2);
q = q1 + 0.5* (q2 - q1);
q = (1/norm(q))* q
[axis, angle] = CL_rot_quat2axAng(q)
SLERP Use example
Here is an exemple on how one can compute LERP in Java language using PATRIUS:
final Vector3D axis = new Vector3D(1,1,1);
final Rotation r1 = new Rotation(axis,FastMath.PI/6.);
final Rotation r2 = new Rotation(axis,FastMath.PI/3.);
final Rotation r = Rotation.slerp(r1, r2, 0.5);
then one can retrieve corresponding rotation angle and axis:
final double rangle = r.getAngle();
final Vector3D raxis = r.getAxis();
Same example given in Scilab using Celestlab macros library:
alpha1 = CL_deg2rad(30.);
q1 = CL_rot_axAng2quat([1;1;1],alpha1);
alpha2 = CL_deg2rad(60.);
q2 = CL_rot_axAng2quat([1;1;1],alpha2);
q = CL_rot_quatSlerp(q1,q2,.5);
[axis, angle] = CL_rot_quat2axAng(q)
Contents
Interfaces
None as of now.
Classes
The relevant classes are :
| Class | Summary | Javadoc |
|---|---|---|
| Quaternion | This class implements quaternions. | ... |
| Rotation | This class implements rotations in a three-dimensional space. | ... |
| RotationOrder | This class is a utility representing a rotation order specification for Cardan or Euler angles specification. | ... |