User Manual 4.0 Planes : Différence entre versions

Version actuelle en date du 5 avril 2018 à 07:30

Definition

The planes are defined by an origin point and a local frame, the W vector being the normal to the plane.

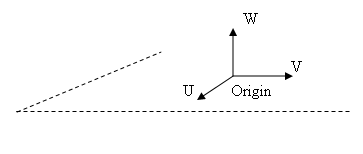
Implementation

The Plane object in the SIRIUS library implements the infinite shape interface . Please refer to the Plane javadoc for a complete list of public methods.

Instantiation

The Plane class (geometry.euclidian.threed) has several constructors :

• One needing one point of the plane and its normal. The Origin point (the closest one to 0,0,0) and the local frame are then computed.

Vector3D normal = new Vector3D(7.2,-2.4, -5.8);
Vector3D orig = new Vector3D(0, 2, 7);
Plane    p  = new Plane(orig , normal);

• One needing three different points of the plane. The Origin point (the closest one to 0,0,0) and the local frame are then computed.

Vector3D p1 = new Vector3D(1.2, 3.4,-5.8);
Vector3D p2 = new Vector3D(3.4,-5.8, 1.2);
Vector3D p3 = new Vector3D(-2.0, 4.3, 0.7);
Plane    p  = new Plane(p1, p2, p3);

• One needing a line and a point belonging to the plane. The Origin point (the closest one to 0,0,0) and the local frame are then computed.

Vector3D point= new Vector3D(2,-8, 4);
Line line = new Line(origin, direction);
Plane    p  = new Plane(point, line);

• One needing a line and a direction vector. The Origin point (the closest one to 0,0,0) and the local frame are then computed.

Vector3D vector = new Vector3D(5, 22,-7);
Line line = new Line(origin, direction);
Plane    p  = new Plane(line, vector);

• One needing one point of the plane, two direction vectors and a boolean (isFrame) to decide if the frame must be computed (like it is done for the rest of the constructors) or if the given point and vectors must constitute the local frame. If this boolean is true, the first given vector is U, the second V : they may not be orthogonal.

Vector3D orig = new Vector3D(0, 2, 7);
Vector3D v1 = new Vector3D(3, 1, 0);
Vector3D v2 = new Vector3D(0, 2, 0);
 
Plane p = new Plane(orig, v1, v2, false);

• One needing only the normal vector. The created plane contains the origin(0, 0, 0)

Vector3D normal = new Vector3D(7.2,-2.4, -5.8);
Plane    p  = new Plane(normal);

• One copy constructor

Plane    p1  = new Plane(p2);

Usage

It provides methods to compute :

• the point resulting of the intersection of three planes (static method)

Vector3D point = Plane.intersection(p1, p2, p3);

• the line resulting of the intersection of two planes

Line line = p1.intersection(p2);

• the point resulting of the intersection of the plane and a line

Vector3D point = p1.intersection(line);

• the distance between a point and the plane (zero if the point belongs to the plane)

double distance = p.distanceTo(point);

• the comparison to another plane (they are similar if they contain the same points) :

boolean similarPlanes = plane1.isSimilarTo(plane2);

• the test of the belonging of a point to the plane

boolean isInThePlane = p.contains(point);

• the distance between a line and the plane (not zero only if the line does not intersect the plane)

double distance = p.distanceTo(line);

• the coordinates of the projection of any point of space in the local frame

Vector2D pointInPlane = p1.toSubSpace(point);

• the coordinates in the global frame of a point expressed in the local frame

Vector3D point = p1.toSpace(pointInPlane);

• translation and rotation of the plane

Plane p2 = p1.rotate(center, rotation);

Plane p2 = p1.translate(vector);

Please refer to the [MAT_GEO_Home#HInteractions Interactions with other geometrical objects section] for methods inherited from the Shape interface.