User Manual 4.2 Numerical differentiation and integration : Différence entre versions
(Page créée avec « __NOTOC__ == Introduction == === Scope === This section détails numerical differentialtion and integration (not to be misunderstood with numerical integration of ODE). A... ») |
(Aucune différence)
|
Version actuelle en date du 14 janvier 2019 à 14:58
Introduction
Scope
This section détails numerical differentialtion and integration (not to be misunderstood with numerical integration of ODE). A focus is realised on:
- differentiation methods of real univariate functions: Ridders and finite difference.
- integration methods of real univariate functions : Trapezoidal and Simpson.
Javadoc
The numerical differentiator objects are available in the package fr.cnes.sirius.patrius.math.analysis.differentiation.
The numerical integrator objects are available in the package fr.cnes.sirius.patrius.math.analysis.integration.
| Library | Javadoc |
|---|---|
| Patrius | Package fr.cnes.sirius.patrius.math.analysis.differentiation |
| Patrius | Package fr.cnes.sirius.patrius.math.analysis.integration |
Links
Links to the implemented integration methods :
http://mathworld.wolfram.com/TrapezoidalRule.html
http://mathworld.wolfram.com/SimpsonsRule.html
Useful Documents
None as of now.
Package Overview
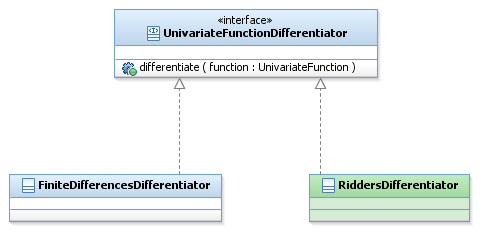
The numerical differentiation conception is described hereafter :
Accuracy of integration method (all examples are based on sinus function):
| Default setting | Value |
|---|---|
| Maximum absolute error | 1.0e-15 |
| Maximum relative error | 1.0e-6 |
| Maximum number of iterations | 64 |
| Minimum number of iterations | 3 |
Note : the accuracy of the results and the computing time are directly dependent on the value of maximum relative error.
Features Description
Numerical differentiation
Finite difference
Finite difference is the discrete analog of the derivative. The user can choose the number of points to use and the step size (the gap between each point).
Ridders algorithm
The derivative of a function at a point x is computed using the Ridders method of polynomial extrapolation.
Numerical Integration
Trapezoidal method
The trapezoidal rule works by approximating the region under the graph of the function as a trapezoid and calculating its area.
UnivariateFunction f = new SinFunction(); UnivariateIntegrator integrator = new TrapezoidIntegrator(); double r = integrator.integrate(10000, f, 0, FastMath.PI);
Result : r = 1.9999996078171345 (exact result = 2)
And :
integrator = new TrapezoidIntegrator(1.e-12, 1.0e-15, 3, 64); r = integrator.integrate(10000000, f, 0, FastMath.PI);
Result : r = 1.9999999999904077
But :
integrator = new TrapezoidIntegrator(1.e-13, 1.0e-15, 3, 64); r = integrator.integrate(10000000, f, 0, FastMath.PI);
Result : r = no result (infinite time !)
Simpson method
Simpson's rule is a Newton-Cotes formula for approximating the integral of a function using quadratic polynomials (i.e., parabolic arcs instead of the straight line segments used in the trapezoidal rule). In general, this method has faster convergence than the trapezoidal rule for functions which are twice continuously differentiable, though not in all specific cases.
UnivariateFunction f = new SinFunction(); UnivariateIntegrator integrator = new SimpsonIntegrator(); double r = integrator.integrate(10000, f, 0, FastMath.PI);
Result : r = 2.000000064530001 (exact result = 2)
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| UnivariateFunctionDifferentiator | This interface represents a generic numerical differentiator. | ... |
| UnivariateIntegrator | Interface for univariate integration algorithms. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| FiniteDifferencesDifferentiator | Apply the finite difference method to differentiate a function. | ... |
| RiddersDifferentiator | Apply the Ridders algorithm to differentiate a function. | ... |
| TrapezoidIntegrator | The class implements the Trapezoidal rule | ... |
| SimpsonIntegrator | The class implements the Simpson rule | ... |