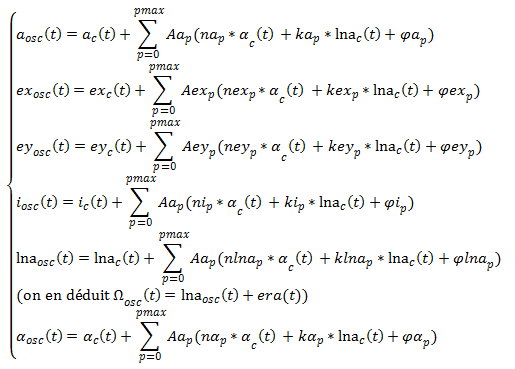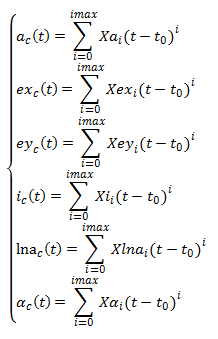User Manual 4.7 Analytical propagation : Différence entre versions
(Page créée avec « == Introduction == === Scope === This section describes the analytical propagators (Keplerian, Eckstein-Hechler, 2D...) provided by the Patrius library. It also explains s... ») |
(Aucune différence)
|
Version du 7 mai 2021 à 07:43
Sommaire
- 1 Introduction
- 2 Features Description
- 3 Getting Started
- 4 Contents
Introduction
Scope
This section describes the analytical propagators (Keplerian, Eckstein-Hechler, 2D...) provided by the Patrius library. It also explains some interpolation algorithms, like the Hermite or Lagrange interpolation for ephemeris and the covariance matrix interpolation. Generic features about propagators as well as other types of propagators are detailed [ORB_PGEN_Home here].
Javadoc
Some of the propagation packages available in the Patrius library are listed here :
Links
None as of now.
Useful Documents
None as of now.
Package Overview
None as of now.
Features Description
Analytical propagators can be defined without any AttitudeProvider.
KeplerianPropagator extrapolator = new KeplerianPropagator(initialOrbit);
In that case, the methods getAttitudeProvider, getAttitudeProviderForces or getAttitudeProviderEvents will return a null-value. If propagation is performed using a propagator defined without any AttitudeProvider, the final SpacecraftState will have a null attitude value.
A single AttitudeProvider could be added to the propagator:
extrapolator.setAttitudeProvider(attProvider);
or two AttitudeProvider for forces and events computation could be added :
extrapolator.setAttitudeProviderForces(attProviderForces); extrapolator.setAttitudeProviderEvents(attProviderEvents);
It is also possible to directly declare the propagator with a single AttitudeProvider :
KeplerianPropagator extrapolator = new KeplerianPropagator(initialOrbit, attProvider);
or two AttitudeProvider for forces and events computation :
KeplerianPropagator extrapolator = new KeplerianPropagator(initialOrbit, attProviderForces, attProviderEvents);
Keplerian propagator
When no perturbing forces are considered in the physical model, the Gauss equations can be resolved analytically. Indeed, the mean anomaly is the only parameter subject to a linear variation with time. Of course, this case is unrealistic, usually several perturbing forces act on the spacecraft and the propagation of the spacecrafts state with a keplerian propagator leads to a rough estimate. The Keplerian orbit propagator is to be used as follows :
double mu = 3.9860047e14; AbsoluteDate initDate = AbsoluteDate.J2000_EPOCH.shiftedBy(584.); Orbit initialOrbit = new KeplerianOrbit(7209668.0, 0.5e-4, 1.7, 2.1, 2.9, 6.2, PositionAngle.TRUE, FramesFactory.getEME2000(), initDate, mu); // Extrapolator definition KeplerianPropagator extrapolator = new KeplerianPropagator(initialOrbit); // Extrapolation at a final date different from initial date double delta_t = 100000.0; // extrapolation duration in seconds AbsoluteDate extrapDate = initDate.shiftedBy(delta_t); SpacecraftState finalOrbit = extrapolator.propagate(extrapDate);
Eckstein-Hechler propagator
The Eckstein-Hechler propagatorEcksteinHechlerPropagator is suited for near circular orbits (eccentricity < 0.1; best results if eccentricity < 0.005) with non-critical inclination (inc. different from ~63.43 deg and ~116.57 deg with a recommended margin of 0.5 deg). When the input orbit consists of mean elements, an inclination of 0 is permitted. However inclination must be higher than 1.e-3 deg for osculating elements (this is required for a good convergence of the transformation from osculating to mean elements).
The model only considers the effects of the following zonal harmonics : J2, J3, J4, J5, J6. The mean elements include secular and long-period effects. The propagation frame has to be nearly inertial, and an equatorial one is recommended (e.g. CIRF).
The central attraction coefficient used in the integration process and given to the propagator can be different from the one associated to the orbit.
Reference: A reliable derivation of the perturbations due to any zonal and tesseral harmonics of the geopotential for nearly-circular satellite orbits, M. C. Eckstein, F. Hechler, ESRO SR-13-1970, ESA, Darmstadt, Germany, 1970.
The Eckstein-Hechler orbit propagator is to be used as follows :
double muOrbit = 3.9860047e14; double ae = 6.378137e6; double c20 =-1.08263e-3; double c30 = 2.54e-6; double c40 = 1.62e-6; double c50 = 2.3e-7; double c60 =-5.5e-7; AbsoluteDate initDate = AbsoluteDate.J2000_EPOCH.shiftedBy(584.); Orbit initialOrbit = new KeplerianOrbit(7209668.0, 0.5e-4, 1.7, 2.1, 2.9, 6.2, PositionAngle.TRUE, FramesFactory.getEME2000(), initDate, muOrbit); // Extrapolator definition EcksteinHechlerPropagator extrapolator = new EcksteinHechlerPropagator(initialOrbit, ae, muIntegration, FramesFactory.getCIRF(), c20, c30, c40, c50, c60, ParametersType.OSCULATING); // Extrapolation at a final date different from initial date double delta_t = 100000.0; // extrapolation duration in seconds AbsoluteDate extrapDate = initDate.shiftedBy(delta_t); SpacecraftState finalOrbit = extrapolator.propagate(extrapDate);
When providing osculating parameters, the propagator will internally compute mean parameters. This requires a threshold which can be tuned with the static method setThreshold. Beware this method and the threshold are static hence it applies to all instances of Ecktein-Hechler propagators.
Warning: if the frame in which model coefficients are expressed is not inertial (ex: TIRF or ITRF), then an exception is thrown.
J2 secular propagator
The J2 secular propagator J2SecularPropagator is an analytical propagator taking into account only mean secular effects of [math]J_2[/math] of central body.
This model only includes the secular effects on argument of perigee, right ascension of ascending node and mean anomaly due to J2. It is valid for elliptical (including circular) orbits only. The main asset (in comparison with more accurate models) is that the model can be used for any orbit , including orbits with near critical inclination and equatorial orbits.
This propagator is to be used as follow:
// Initialization final double mu = 3.9860047e14; final double ae = 6.378137e6; final double c20 =-1.08263e-3; final Frame frame = FramesFactory.getCIRF(); final AbsoluteDate date = AbsoluteDate.J2000_EPOCH; final Orbit initialOrbit = new KeplerianOrbit(7209668.0, 0.5e-4, 1.7, 2.1, 2.9, 6.2, PositionAngle.TRUE, FramesFactory.getEME2000(), date, mu); // Simple propagation (slave mode) J2SecularPropagator propagator = new J2SecularPropagator(initialOrbit, ae, mu, c20, frame); final AbsoluteDate finalDate = date.shiftedBy(1000.); SpacecraftState finalOrbit = propagator.propagate(finalDate);
Warning: if the frame in which model coefficients are expressed is not inertial (ex: TIRF or ITRF), then an exception is thrown. The frame should be an inertial or quasi-inertial frame in which the model is supposed valid, the Z axis of the frame being the polar axis of the body.
Lyddane propagators
Lyddane propagators LyddaneSecularPropagator and LyddaneLongPeriodPropagator are analytical propagators providing different mean elements: only secular effects for the former, secular plus long period ones for the latter. They only consider the effects of J2, J3, J4, J5 zonal harmonics. The propagation frame has to be nearly inertial, and an equatorial one is recommended (e.g. CIRF). When osculating elements are provided as input to LyddaneSecularPropagatorand LyddaneLongPeriodPropagator, the osculating orbits that results from propagation are identical.
Lyddane propagators arenot to be used:
- for orbits whose eccentricity is larger than 0.9.
- for orbits whose inclination is close to the critical one (~63.43 deg and ~116.57 deg with a recommended margin of at least 0.5 deg).
These propagators are to be used as follow:
// Initialization final double mu = 3.9860047e14; final double ae = 6.378137e6; final double c20 =-1.08263e-3; final double c30 = 0.000002532393; final double c40 = 0.000001619137; final double c50 = 0.000000227742; final Frame frame = FramesFactory.getCIRF(); final AbsoluteDate date = AbsoluteDate.J2000_EPOCH; final Orbit initialOrbit = new KeplerianOrbit(7209668.0, 0.5e-4, 1.7, 2.1, 2.9, 6.2, PositionAngle.TRUE, FramesFactory.getEME2000(), date, mu); // Simple propagation (slave mode) LyddaneSecularPropagator propagator = new LyddaneSecularPropagator(initialOrbit, ae, mu, c20, c30, c40, c50, frame); final AbsoluteDate finalDate = date.shiftedBy(1000.); SpacecraftState finalOrbit = propagator.propagate(finalDate);
LyddaneLongPeriodPropagator is used exactly in the same manner.
When providing osculating parameters, the propagator will internally compute mean parameters. This requires a threshold which can be tuned with the static method setThreshold. Beware the threshold is static hence it applies to all instances of Ecktein-Hechler propagators.
Warning: if the frame in which model coefficients are expressed is not inertial (ex: TIRF or ITRF), then an exception is thrown. The frame should be an inertial or quasi-inertial frame in which the model is supposed valid, the Z axis of the frame being the polar axis of the body.
TLE propagator
Two TLE propagators are available :
- SGP4
- SDP4
The choice amongst them must be made on the value of the period of the orbit. The static selectExtrapolator method of the TLEPropagator realize it from the TLE object and return the right propagator, initialized with that TLE.
From that point, the TLE propagator shall be used as any propagator (but the initial state can't be reseted : to propagate another TLE, a new propagator must be created).
// TLE to propagate final TLE ISS_TLE = new TLE(line1ISS, line2ISS); // Start date of the propagation : date of the TLE final AbsoluteDate startDate = ISS_TLE.getDate(); // propagator final Propagator propagator = TLEPropagator.selectExtrapolator(ISS_TLE); // propagation duration and end date final double duration = 20000.; final AbsoluteDate endDate = startDate.shiftedBy(duration); // propagation SpacecraftState endState = propagator.propagate(endDate );
Analytical 2D Propagator
This propagator expresses each circular osculating parameter as the sum of a "centered part" and a trigonometric polynomial. The former represents the secular effects of the potential attraction whilst the latter represents its osculating effects.
This propagator is designated as two-dimensional because each orbital parameter depends on both the mean latitude argument and the mean longitude of the ascending node. Because the osculating effects are embodied in the trigonometric part, this propagator is well suited for phased orbits.
For each circular parameter (a, ex, ey, i, lna, [math]\alpha[/math]), the formulas used are:
The "centered" part
The "centered" part is any function having one variable : the date. It is represented by an object of type UnivariateDateFunction.
At this time, the following univariate functions are available :
- piecewise functions of date which are reprensented by the extensions of AbstractDateIntervalFunction :
- polynomial functions of date
The trigonometric polynomial part
For each circular parameter (a, ex, ey, i, lna, [math]\alpha[/math]), the formula of the trigonometric polynomial part used is:
where [math]\alpha_C[/math] and [math]l_{NAC}[/math] represent the secular evolution of the latitude argument and longitude of the ascending node. This secular evolution corresponds to the "centered part" of the respective parameter models.
with [math]A(p)[/math] and [math]\Phi(p)[/math] respectively being the trigonometric amplitude and phase.
The right ascension of ascending node and its mean longitude are connected as per the following equation :
where [math]\theta[/math] represent the Earth rotation angle and [math]\Omega[/math] the polynomial part of the right ascension of ascending node.
The analytical 2D propagator model
The Analytical2DParameterModel is an object that represents one parameter. It contains the [math]\alpha_i[/math] and [math]l_i[/math], [math]A(p)[/math],[math]\Phi(p)[/math] coefficients and the "centered" part for said parameter. It also provides all the methods required to propagate the parameter to a specific date. At instanciation time, it is assumed that the trigonometric entries are listed in the user specified table with decreasing amplitudes.
The Analytical2DOrbitModel represents an orbital 2D model, made up of 6 Analytical2DParameterModel (one for each of a, ex, ey, i, lna, [math]\alpha[/math]).
The Analytical2DPropagatorModel allows connecting this propagation model to the Patrius propagation model, that supports events detection etc. As such, it only calls the propagateModel method of its inner field Analytical2DOrbitModel.
The following example shows how to create an instance of a Analytical2DPropagatorModel.
// Create "centered part" final double[] coefs = { 2., 3., 4., 5. }; final DatePolynomialFunction polynomialFunction = new DatePolynomialFunction(originDate, coefs); // Example for sma, same for ex, ey, i, lna and alpha final Analytical2DParameterModel smaModel = new Analytical2DParameterModel(polynomialFunction, trigonometricCoefs); // Create an orbit model out of the parameter model- use user given pso and lna tables final Analytical2DOrbitModel orbitPsoLna = new Analytical2DOrbitModel(smaModel, ex, ey, i, lna, alpha, mass, mu); // Create the propagator Analytical2DPropagator propPsoLna = new Analytical2DPropagator(orbitPsoLna, originDate); // Propagation SpacecraftState state = propPsoLna.propagate(targetDate); Orbit orbit = state.getOrbit();
Precomputed ephemeris
These pseudopropagators are bounded and based on a set of ephemerides :
- Integrated Ephemeris : With the ephemeris generation mode, a bounded propagator is available at the end of the numerical propagation and gives access to the orbit state at any date inside the propagation time interval. These intermediate states are computed thanks to the object IntegratedEphemeris. This object stores for each step the interpolator used, during the integration.
- Ephemeris : Another class is available for the same purpose (access to the orbit state at any given date): the Ephemeris class. An instance is built from a list of spacecraft states - that is to say, discrete ephemeris. Here, the intermediate states (keplerian, cartesian, ... parameters, depending on the kind of Orbit used) are computed with Hermite interpolators, which provides less accuracy than with the IntegratedEphemeris object. But for most uses, notably event detection, the Ephemeris class appears reliable enough.
- Lagrange Ephemeris and Hermite Ephemeris : These class are deprecated since 3.1. They were extending AbstractPropagator and they were computing propagation using Lagrange or Hermite interpolation between spacecraftstates. These possibilities has been replaced by the use of a simple propagator based on a PVCoordinateProvider which compute position, velocity with a Lagrange or Hermite interpolation between position, velocity ephemeris. This way of propagation is described in [ORB_Ephemeris_Home Ephemeris] page.
Covariance matrix propagation
The purpose of this interpolation algorithm is to compute the covariance matrix at a given date through a simplified model of the transition matrix. When a covariance in PV coordinates is searched for an object orbiting around an celestial body, a simple dynamical model can be used, meaning limited to the newtonian attraction, plus a constant acceleration. The value of this constant acceleration will not change the transition matrix.
The transition matrix between a date [math]t_1[/math] and a date [math]t[/math] can be approximated :
- at order 0 : by [math]\phi_1(t_1, t) = I_{3 \times 3}[/math]
- at order 1 : by [math]\phi_1(t_1, t) = I_{3 \times 3} + J_{PV} ( t- t_1)[/math]
- at order 2 : by[math]\phi_1(t_1, t) =I_{3 \times 3} + J_{PV} ( t- t_1)+ 0.5 * J_{PV}^2 ( t - t_1)^2[/math]
where [math]J_{PV} = \left(\begin{array}{cc} 0_{3 \times 3} & I_{3 \times 3} \\ A & 0_{3 \times 3} \end{array} \right)[/math], [math]J_{PV}^2 = \left(\begin{array}{cc} A & 0_{3 \times 3} \\ 0_{3 \times 3} & A \end{array} \right)[/math] and [math]A =- \frac{ GM}{r^3}\left(I_{3 \times 3} - 3 \frac{ PP^T}{r^2}\right)[/math], where [math]A[/math] is considered as a constant on the interval [math][t_1,t][/math] and [math]P[/math] is the satellite position vector.
We denote by [math]M(t)[/math] the covariance matrix at instant t. Let [math]t \in [t_1,t][/math] . The transition matrices [math]\phi_1(t_1, t)[/math] and [math]\phi_2(t_2, t)[/math] are given by the above formula, and since matrix [math]A[/math] is constant on [math][t_1,t_2][/math], we have that the covariance matrix at instant [math]t[/math] is given by
[math]M(t) = (1- \alpha) \phi_1(t_1, t) M(t_1)\phi_1^T(t_1, t) + \alpha \phi_2(t_2, t) M(t_2)\phi_2^T(t_2, t),[/math]
with [math]\alpha = \frac{t-t_1}{t_2-t_1}[/math].
Other features of analytical propagators
Mean/osculating elements conversion
Some analytical propagators extend the MeanOsculatingElementsProvider interface. As a result these analytical propagators provide the three following methods:
-
Orbit osc2mean(final Orbit orbit): conversion from osculating parameters to mean parameters using the underlying theory. -
Orbit mean2osc(final Orbit orbit): conversion from mean parameters to osculating parameters using the underlying theory. -
Orbit propagateMeanOrbit(final AbsoluteDate date): provides the mean orbital parameters at required date using the underlying theory.
Warning: Used algorithm for osculating to mean conversion often consists in an iterative algorithm with a convergence criterion. As a result convergence is not always ensured, depending on the underlying theory. Static method setThreshold() allows the user to change the convergence threshold if convergence issues arise.
Example of convergence issues: Lyddane propagators fails to return mean elements from the following Keplerian osculating elements: [a = 24400km, e = 0.72, i = 0 deg, gom = 0 deg, pom = 0 deg, M = 0.1 deg].
Currently available mean <=> osculating conversions are:
- Lyddane (both long period and secular)
- Eckstein-Hechler
- Liu
- Analytical 2D Orbit model and propagator
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| Propagator | This interface provides a way to propagate an orbit at any time. | ... |
| MeanOsculatingElementsProvider | This interface provides mean <=> osculating elements conversion. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| AbstractPropagator | Common handling of Propagator methods for analytical propagators. | ... |
| SpacecraftState | This class is the representation of a complete state holding orbit, attitude for forces and for events computation and additional states at a given date. | ... |
| TLE | This class is a container for a single set of TLE data. | ... |
| KeplerianPropagator | Simple keplerian orbit propagator. | ... |
| EcksteinHechlerPropagator | This class propagates a SpacecraftState using the analytical Eckstein-Hechler model. | ... |
| J2SecularPropagator | This class propagates a SpacecraftState using the analytical J2 secular model. | ... |
| LyddaneSecularPropagator | This class propagates a SpacecraftState using the analytical Lyddane secular model. | ... |
| LyddaneLongPeriodPropagator | This class propagates a SpacecraftState using the analytical Lyddane secular + long period model. | ... |
| LiuMeanOsculatingConverter | This class provides a mean <=> osculating elements conversion following Liu theory. | ... |
| Analytical2DParameterModel | This class represent an orbital parameter model to use with a Analytical2DPropagator | ... |
| Analytical2DOrbitModel | This class represent an orbit model to use with a Analytical2DPropagator | ... |
| Analytical2DPropagator | This class represents a 2D propagator. | ... |
| TLEPropagator | This class provides elements to propagate TLE's. | ... |
| Ephemeris | This class is designed to accept and handle tabulated orbital entries. Tabulated entries are classified and then extrapolated in way to obtain continuous output, with accuracy and computation methods configured by the user. | ... |
| EphemerisPvLagrange | This class handles tabulated spacecraft states entries and implements PVCoordinatesProvider interface. Tabulated entries are chronologically classified. A Lagrange interpolation is perfomed to compute PV coordinates at a given date. | ... |
| EphemerisPvHermite | This class handles tabulated spacecraft states entries and implements PVCoordinatesProvider interface. Tabulated entries are chronologically classified. A Hermite interpolation is perfomed to compute PV coordinates at a given date. | ... |
| PVCoordinatePropagator | This class extends AbstractPropagator. It simply implements propagate orbit method using the getPVCoordinate from the PVCoordinate provider it handles. The propagator is initialized with given initial date, frame and mu to build a coherent initial spacecraftstate. This initialisation calls the PVCoordinateprovider getPvCoordinate method to the given date which can raise an error if the date is out of bound for exemple. This class will be basically used with EphemerisPvLagrange and EphemerisPvHermite. | ... |