« User Manual 4.13 Projections » : différence entre les versions
Page créée avec « == Introduction == === Scope === The scope of this section is to present the projections features available in Patrius library. Patrius provides classes to perform project... » |
Aucun résumé des modifications |
||
| Ligne 118 : | Ligne 118 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth"); | ||
final Mercator projection = new Mercator(0., ellipsoid); | final Mercator projection = new Mercator(0., ellipsoid); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Ligne 127 : | Ligne 127 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidPoint toulouse = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.758011794, 0.026140528, 256., "toulouse"); | ||
final Vector2D projectedPoint = projection.applyTo(toulouse); | final Vector2D projectedPoint = projection.applyTo(toulouse); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Ligne 134 : | Ligne 134 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidPoint geodeticCoordinates = projection.applyInverseTo(projectedPoint.getX(), projectedPoint.getY()); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Ligne 142 : | Ligne 142 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth"); | ||
final Mercator projection = new Mercator(0., ellipsoid); | final Mercator projection = new Mercator(0., ellipsoid); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Ligne 151 : | Ligne 151 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidPoint toulouse = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.758011794, 0.026140528, 256., "toulouse"); | ||
final | final EllipsoidPoint london = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.898844565, 0.002268928, 25., "london"); | ||
final Vector2D projectedToulouse = projection.applyTo(toulouse); | final Vector2D projectedToulouse = projection.applyTo(toulouse); | ||
final Vector2D projectedLondon = projection.applyTo(london); | final Vector2D projectedLondon = projection.applyTo(london); | ||
| Ligne 161 : | Ligne 161 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final List<EllipsoidPoint > list = new ArrayList<>(); | |||
final List< | |||
list.add(toulouse); | list.add(toulouse); | ||
list.add(london); | list.add(london); | ||
| Ligne 176 : | Ligne 174 : | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
final | final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth"); | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Dernière version du 21 décembre 2023 à 14:29
Introduction
Scope
The scope of this section is to present the projections features available in Patrius library. Patrius provides classes to perform projections on an ellipsoid as well as various computation on the surface of an ellipsoid. Common available projections are:
- Mercator
- Flamsteed-Samson
- Identity projection
Javadoc
All the classes related to projections are in the following packages:
| Library | Javadoc |
|---|---|
| Patrius | Package fr.cnes.sirius.patrius.projections |
Links
More information about specific projections can be found using the following links:
Useful Documents
None as of now.
Package Overview
The projections package gathers:
- An interface for all projections:
IProjection - Some available projections :
Mercator,GeneralizedFlamsteedSamsonandIdentityProjection - A ellipsoid with extended features:
ProjectionEllipsoid
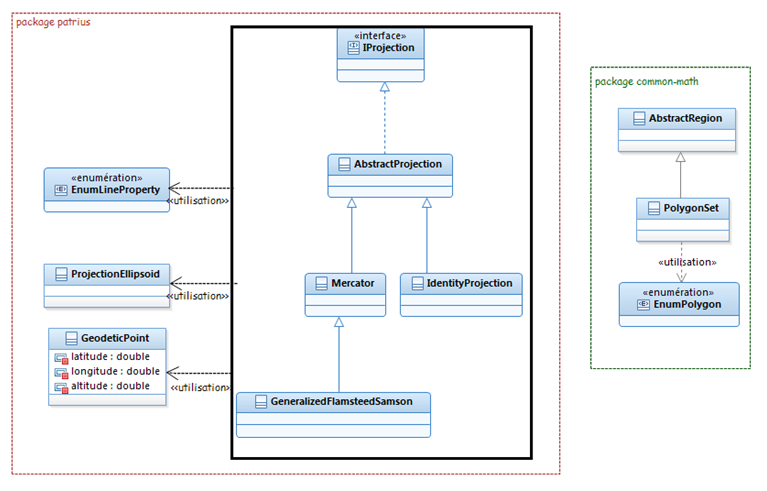
The projection package can be summarized with the following UML diagram.
Please note that not all implementations are present in the following diagram for the sake of clarity.
Features Description
Projections provide three main features:
- Projection on an ellipsoid (and its inverse application)
- Discretisation between points on the surface of an ellipsoid
- Geometric computation on the surface of an ellipsoid using class ProjectionEllipsoid
Projection on an ellipsoid
Projection on an ellipsoid is a transformation taking geodetic coordinates (latitude, longitude, altitude) as input and returning 2D map coordinates (X, Y) as output. Inverse transformation takes 2D map coordinates (X, Y) as input and returns geodetic coordinates (latitude, longitude, altitude) as output.
Projection classes inherit projection interface IProjection.
Available projections are:
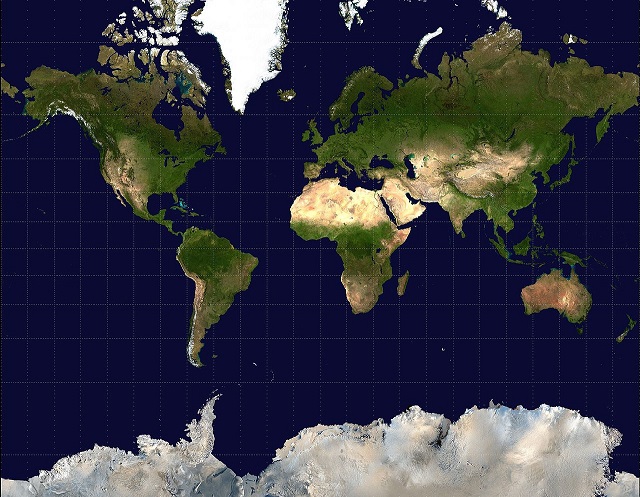
- Mercator projection:
Mercator. The Mercator projection is a cylindrical map projection which became the standard map projection for nautical purposes because of its ability to represent lines of constant course, known loxodromes, as straight segments. Mercator projection is conformal (angles are preserved) but not equivalent (areas are not preserved).
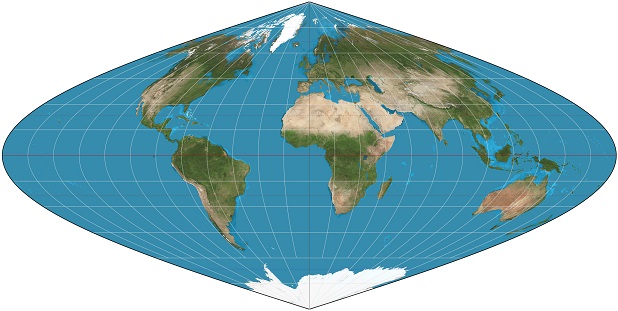
- Flamsteed-Samson projection:
GeneralizedFlamsteedSamson. This projection is also known as the sinusoidal projection. The sinusoidal projection is equal-area and preserves distances along the horizontals but is not conformal (angles are not preserved).
- Identity projection:
IdentityProjection. Identity projection is the projection [latitude, longitude, altitude] => [X = latitude, Y = longitude].
All projections provide:
- direct transformation using method
applyTo(). It returns 2D map coordinates (X, Y) from geodetic coordinates (latitude, longitude, altitude). - inverse transformation using method
applyInverseTo(). It returns geodetic coordinates (latitude, longitude, altitude) from 2D map coordinates (X, Y).
Discretization
All projection classes provide various discretization methods between geodetic points.
- Discretization between two projected points using the method
discretize(). Maximum distance between discretized point has to be provided. - Discretization along a polygon line of geodetic coordinates using the method
discretizeAndApplyTo(). Maximum distance between discretized point has to be provided as well as the discretization strategy.
The discretization strategy is provided with the enumeration EnumLineProperty. It offers the following possibilities:
STRAIGHT: straight line between two geodetic points.GREAT_CIRCLE: arc being the shortest way to connect two geodetic points on an ellipsoid. The center of the ellipsis is the ellipsoid center.STRAIGHT_RHUMB_LINE: arc between two geodetic points crossing all meridians of longitude at the same angle. It corresponds to a path of constant bearing as measured relative to true north. On Mercator projection, it is represented by a straight line.
Other methods are available. For more information, refer to the javadoc of AbstractProjection class.
Computation on the surface of an ellipsoid
A specific ellipsoid class has been defined to handle projections: ProjectionEllipsoid. This class inherits the class OneAxisEllipsoid.
It provides many useful projection-related computations on the surface of an ellipsoid.
Available features of ProjectionEllipsoid are:
- Distance computation:
Orthodromic distance using method computeOrthodromicDistance(). Orthodromic distance is the shortest path between two points.
Loxodromic distance using method computeLoxodromicDistance(). Loxodromic distance follows path of constant bearing: this is a straight line on Mercator projection.
Meridional distance using method computeMeridionalDistance(). Meridional distance is the shortest distance from one point to the equator (along a meridian).
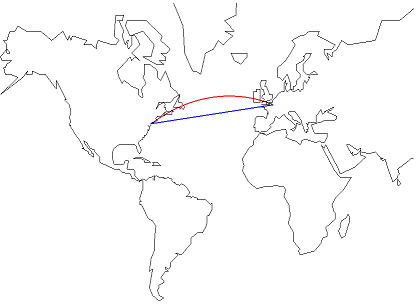
On next image, Loxodromic distance is in red, orthodromic distance in blue:
- Azimuth computation:
Bearing using method computeBearing().
Spherical azimuth using method computeSphericalAzimuth().
- Other computations:
Point along loxodrome, given a point, a distance from this point and an azimuth from this point, using method computePointAlongLoxodrome().
Point along orthodrome, given a point, a distance from this point and an azimuth from this point, using method computePointAlongOrthodrome().
Other methods are available. For more information, refer to the javadoc of ProjectionEllipsoid class.
Getting Started
Projections provide three main features:
- Projection on an ellipsoid (and its inverse application)
- Discretisation between points on the surface of an ellipsoid
- Geometric computation on the surface of an ellipsoid using class
ProjectionEllipsoid
Projection on an ellipsoid
First an ellipsoid and a projection have to be defined, here using a simple centered Mercator projection:
final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth");
final Mercator projection = new Mercator(0., ellipsoid);
Then the created projection can be used in different ways:
- Projection of geodetic coordinates:
final EllipsoidPoint toulouse = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.758011794, 0.026140528, 256., "toulouse");
final Vector2D projectedPoint = projection.applyTo(toulouse);
- Retrieve geodetic coordinates from Mercator 2D coordinates:
final EllipsoidPoint geodeticCoordinates = projection.applyInverseTo(projectedPoint.getX(), projectedPoint.getY());
Discretization
First an ellipsoid and a projection have to be defined, here using a simple centered Mercator projection:
final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth");
final Mercator projection = new Mercator(0., ellipsoid);
Then the created projection can be used in different ways:
- Discretization between two projected points with a maximum distance between points of 1km:
final EllipsoidPoint toulouse = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.758011794, 0.026140528, 256., "toulouse");
final EllipsoidPoint london = new EllipsoidPoint(ellipsoid, LLHCoordinatesSystem.ELLIPSODETIC, 0.898844565, 0.002268928, 25., "london");
final Vector2D projectedToulouse = projection.applyTo(toulouse);
final Vector2D projectedLondon = projection.applyTo(london);
final List<Vector2D> points = projection.discretize(projectedToulouse, projectedLondon, 1000., true);
- Rhumb discretization along a polygon line with a maximum distance between points of 1km followed by projection:
final List<EllipsoidPoint > list = new ArrayList<>();
list.add(toulouse);
list.add(london);
final List<Vector2D> points = projection.discretizeAndApplyTo(list , EnumLineProperty.STRAIGHT_RHUMB_LINE, 1000.);
- etc. Other similar discretization features are available. See javadoc for more information.
Computation on the surface of an ellipsoid
First an ellipsoid has to be defined:
final EllipsoidBodyShape ellipsoid = new OneAxisEllipsoid(6378137.0, 1. / 298.257223563, FramesFactory.getITRF(), "earth");
Then this ellipsoid can be used to:
- Compute distances on the surface of the ellipsoid:
final double orthodromicDistance = ellipsoid.computeOrthodromicDistance(toulouse, london);
final double loxodromicDistance = ellipsoid.computeLoxodromicDistance(toulouse, london);
final double meridionalDistance = ellipsoid.computeMeridionalDistance(toulouse.getLatitude());
- Compute azimuth angles on the surface of the ellipsoid:
final double bearing = ellipsoid.computeBearing(toulouse, london);
final double sphericalAzimuth = ellipsoid.computeSphericalAzimuth(toulouse, london);
- etc. Other similar features are available. See javadoc for more information.
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| IProjection | Interface for projections on a 3D body. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| EnumLineProperty | Enumeration of points connecting strategies on an ellipsoid. | ... |
| IdentityProjection | Identity projection. | ... |
| GeneralizedFlamsteedSamson | Flamsteed-Samson projection. | ... |
| Mercator | Mercator projection. | ... |
| ProjectionEllipsoid | Ellipsoid with extended features (features related to projections). | ... |