User Manual 4.3 Orbits

User Manual 4.3 Orbits

Introduction

Scope

The "orbits" package contains classes to represent the orbital state of a spacecraft at a given time. Several types of orbits are available (cartesian, keplerian, equinoctial...). The jacobian matrix for each orbital parameter / cartesian parameter conversion are also available for their current value.

An "Orbit" (implementing "Orbit" class) object is not to be misunderstood with an "Orbital parameters" object (implement "IOrbitalParameters" interface). An orbit uses as attributes:

• Orbital parameters
• A date
• A frame (not necessarily inertial or pseudo-inertial)

For more information about orbital parameters, please refer to [FDY_PARAM_Home Orbital parameters].

Javadoc

The classes for orbits description are available in the package fr.cnes.sirius.patrius.orbits.

Library	Javadoc
Patrius	Package fr.cnes.sirius.patrius.orbits

Links

None as of now.

Useful Documents

None as of now.

Package Overview

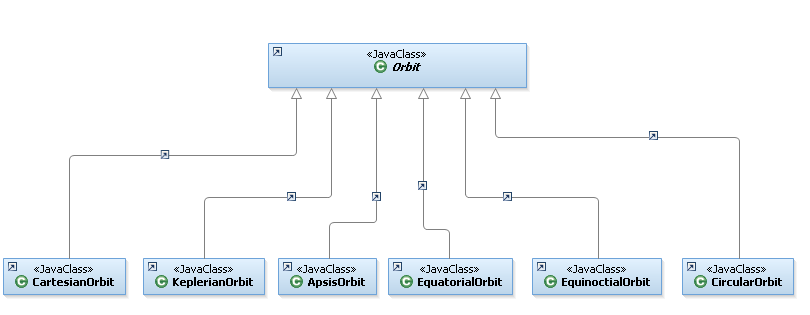
All different orbits types extend the abstract generic Orbit class (the following class package may not contain all classes extending Orbit class).

The enum "PositionAngle" lists the three types of position angle (anomaly, alpha angle...) available : TRUE, MEAN, ECCENTRIC.

Features Description

Available orbit types

The available orbit types are :

• Cartesian  : X, Y, Z, Vx, Vy, Vz
• Keplerian : a, e, i, perigee argument, right ascension of ascending node, anomaly (in each position angle types)
• Equinoctial : a, ex, ey (eccentricity vector), hx, hy (inclination vector), true longitude argument (in each position angle types)
• Alternate equinoctial : n (mean motion), ex, ey (eccentricity vector), hx, hy (inclination vector), longitude argument (in each position angle types, but stored in mean)
• Circular : a, ex, ey (eccentricity vector), i, right ascension of ascending node, true latitude argument (in each position angle types)
• Apsis : periapsis, apoapsis, i, perigee argument, right ascension of ascending node, anomaly (in each position angle types)
• Equatorial : a, e, longitude of the periapsis (ω + Ω), ix (first component of inclination vector), iy (second component of inclination vector), anomaly (in each position angle types)

Jacobians

For each orbital parameter type (keplerian, equinoctial, circular, apsis, equatorial), the jacobian matrices "orbital parameters with respect to cartesian parameters" and "cartesian parameters with respect to orbital parameters" are available. The jacobian matrix related to the conversion between an orbital parameter type A to an orbital parameter type B is also available (computed by getJacobian method) for each orbital parameter type.

For all except the equinoctial and equatorial parameters, the "with respect to cartesian parameters" jacobian (getJacobianWrtCartesian method) is computed with direct analytic methods, and the "with respect to orbital parameters" (getJacobianWrtParameters method) obtained by computing the inverse of the previous one. For the equinoctial and equatorial parameters, both computations are direct and analytic.

Getting Started

Any orbit can be defined using the chosen constructor. Here is an to define a circular orbit:

final KeplerianParameters keplerianParameters = new KeplerianParameters(10000E3, 0.1, 0.2, 0.3, 0.4, 0.5, PositionAngle.TRUE, Constants.EGM96_EARTH_MU);
final CircularOrbit orbit = new CircularOrbit(keplerianParameters, FramesFactory.getEME2000(), date);

Internal parameters of circular orbits are circular parameters. They can be retrieved and converted using conversion routines provided by Orbital parameters objects:

final CartesianParameters cartesianParameters = orbit.getParameters().getCartesianParameters();

Contents

Interfaces

None as of now.

Classes

Class	Summary	Javadoc
Orbit	Abstract class for all orbits.	...
CartesianOrbit	Instant orbit described by its cartesian parameters.	...
KeplerianOrbit	Instant orbit described by its keplerian parameters.	...
CircularOrbit	Instant orbit described by its circular parameters.	...
EquinoctialOrbit	Instant orbit described by its equinoctial parameters.	...
AlternateEquinoctialOrbit	Instant orbit described by its equinoctial parameters.	...
EquatorialOrbit	Instant orbit described by its equatorial parameters.	...
ApsisOrbit	Instant orbit described by its apsis parameters.	...