User Manual 4.7 Celestial bodies

User Manual 4.7 Celestial bodies

Introduction

Scope

This section presents the Trigonometric Polynomials implemented in PATRIUS as well as Fourier Series.

Javadoc

The trigonometric polynomial (and related) objects are available in the package fr.cnes.sirius.patrius.math.analysis.polynomials and the FFT algorithms in fr.cnes.sirius.patrius.math.transform

Library	Javadoc
Patrius	Package fr.cnes.sirius.patrius.math.geometry.analysis.polynomials
Patrius	Package fr.cnes.sirius.patrius.math.transform

Links

Useful resources for this theme can be found here :

• Trigonometric Polynomials
• List of trigonometric identities
• Fourier Series

Useful Documents

None.

Package Overview

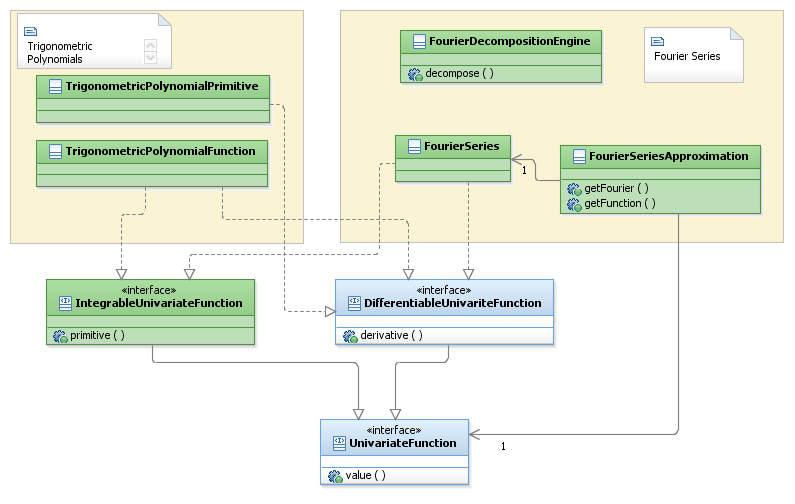
Features Description

Trigonometric Polynomials

The trigonometric polynomials are defined as :

[math]\forall t \in \mathbb{R}, P(t) = a_0 + \sum_{k=0}^n \left( a_k \cos(kt) + b_k \sin(kt) \right)[/math]

And the primitive of such a function is :

[math]\forall t \in \mathbb{R}, P(t) = a_0 t + c^{te} + \sum_{k=0}^n \left( {-b_k \over k} \cos(kt) + {a_k \over k} \sin(kt) \right)[/math]

Classes that represent these functions are described in this section.

Fourier Series

Let [math]f[/math] be a periodic, real variable, real function with period [math]T[/math]. The partial sums of the Fourier Series of [math]f[/math] are given by

[math] \forall N \in \mathbb{R}^{+*}, \, \left(S_Nf\right)(x) = a_0 + \sum_{n=1}^N\left(a_n\cos\left(n t {2\pi\over T}\right) + b_n\sin\left(n t {2\pi\over T}\right)\right) [/math]

The Fourier coefficients (n > 0) of [math]f[/math] are given by :

[math] a_0 = {1\over T}\int_{-T/2}^{T/2} \! f(t) \, \mathrm{d}t [/math]

[math] a_n = {2\over T}\int_{-T/2}^{T/2} \! f(t) \cos\left(n t {2\pi\over T}\right) \, \mathrm{d}t [/math]

[math] b_n = {2\over T}\int_{-T/2}^{T/2} \! f(t) \sin\left(n t {2\pi\over T}\right) \, \mathrm{d}t [/math]

Classes that allow decomposing functions into finite Fourier series are described.

Fast Fourier Transforms

A fast Fourier transform (FFT) is an algorithm to compute the discrete Fourier transform (DFT) and its inverse. Fourier analysis converts time (or space) to frequency and vice versa. An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors.
Let [math]( X_0, ..., X_{N-1})[/math] be complex numbers. The DFT is defined by the formula
[math]X_k = \sum^{N-1}_{n=0} x_n e^{-2i\pi k n/N}, \quad k=\left\{0, ..., N-1\right\}.[/math]

The class FastFourierTransformer.java owns two methods
transform(final double[] f, final TransformType type)
transform(final Complex[] f, final TransformType type)
where TransformType is an enumeration that defines the type of transform which is to be computed. It can be FORWARD or INVERSE.

Depending on the size, this method will use a radix-2 algorithm if the size is a power-of-two, and the Bluestein algorithm otherwise. Both algorithms are explained above.

The Cooley–Tukey & radix-2 the algorithm

By far the most commonly used FFT algorithm. This is a divide and conquer algorithm that recursively breaks down a DFT of any composite size [math]N = N_1N_2[/math] into many smaller DFTs of sizes [math]N_1[/math] and [math]N_2[/math], along with [math]O(N)[/math] multiplications by complex roots of unity.
The radix-2 algorithme is the most common use of FFT algorithm and is based on the Cooley–Tukey algorithm. It divides the transform into two pieces of size [math]N/2[/math] at each step, and is therefore limited to power-of-two sizes.

The Bluestein algorithm

It is commonly called the chirp z-transform algorithm. It computes the discrete Fourier transform (DFT) of arbitrary sizes (including prime sizes) by re-expressing the DFT as a convolution. For more information, see http://en.wikipedia.org/wiki/Bluestein%27s_FFT_algorithm

Getting Started

Usage of a trigonometric polynomial

• To create the polynomial [math]P(x) =-2 + \cos(x) + 2\sin(3x)[/math], use the following code snippet :

double a0 =-2;
double[] a = new double[] {1, 0, 0};
double[] b = new double[] {0, 0, 2};
TrigonometricPolynomialFunction myPol2 = new TrigonometricPolynomialFunction(a0, a, b);

• To get the value of the second derivative at [math]x = 5[/math], use the following snippet :

double result = myPol2.value(2,5);
// equivalent to
double result = myPol2.polynomialDerivative(2).value(5);

• To get the primitive :

// With an integration constant c = 1 :
TrigonometricPolynomialPrimitive result = myPol2.polynomialPrimitive(1.);

• To multiply two trigonometric polynomials [math]p1[/math] and [math]p2[/math] :

TrigonometricPolynomialFunction result = p1.multiply(p2);

Decomposing a UnivariateFunction into a Fourier Series

Given a user function with period T :

UnivariateFunction f = new UnivariateFunction () {
    public double value(double x) {
         // ...
         return result;
    }
};

The user must build an instance of the FourierDecompositionEngine (using an integrator) :

FourierDecompositionEngine engine = new FourierDecompositionEngine( integrator );

And pass the function, period and approximation order to it.NOTE : It is left up to the user to make sure that the specified period is coherent with the function as no internal check is conducted.

engine.setOrder(10);
engine.setFunction(f, T);

Then, the user can call the decompose( ) method :

FourierSeriesApproximation approximation = engine.decompose();
FourierSeries fourier = approximation.getFourier();

Example

The following code snippet shows how to decompose a square function of period 2 to the 10th order :

// function definition
UnivariateFunction function = new UnivariateFunction() {
   public double value(final double x) {
   final double local = x- FastMath.floor(x / 2) * 2;
      if (local >= 1) {
         return-1;
      } else {
         return 1;
      }
   }
};
 
// Engine parameters
UnivariateIntegrator integrator = new LegendreGaussIntegrator(5, 1e-14, 1e-14);
FourierDecompositionEngine engine = new FourierDecompositionEngine(integrator);
engine.setMaxEvals(Integer.MAX_VALUE);
 
// decompose
double period = 2;
engine.setOrder(10);
engine.setFunction(function, period);
FourierSeriesApproximation result = engine.decompose();
FourierSeries fourier = result.getFourier();

The function and its approximation are shown hereunder. The parasite undulations are known as the Gibbs Phenomenon :

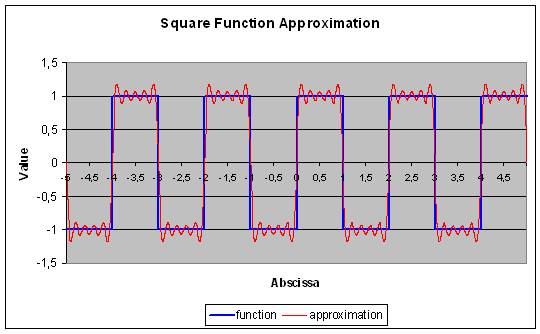
Contents

Interfaces

Interface	Summary	Javadoc
UnivariateDifferentiableFunction	Extension of UnivariateFunction representing a differentiable univariate function.	...
IntegrableUnivariateFunction	Extension of UnivariateRealFunction representing an integrable univariate function.	...
UnivariateFunction	Interface representing an univariate function.	...
IFastFourierTransformer	Interface representing a FFT.	...

Classes

Class	Summary	Javadoc
FourierDecompositionEngine	Decompose a UnivariateFunction as a Fourier Series using TrigonometricPolynomialFunction representation.	...
FourierSeries	This class represents a finite Fourier Series.	...
FourierSeriesApproximation	Holder for a UnivariateFunction and its FourierSeries approximation.	...
TrigonometricPolynomialFunction	This class is the Trigonometric Polynomial Function class.	...
TrigonometricPolynomialPrimitive	This class represents a Trigonometric Polynomial Primitive.	...
AbstractFastFourierTransformer	Abstract class representing a FFT.	[http://patrius.cnes.fr/uploads/JavaDocs/V4.7/fr/cnes/sa Introduction Scope The celestial bodies are described by their main features : position and geometry. The positions are ephemeris that must be loaded from models, the geometries are created as one axis ellipsoids. The package provides a factory able to create any celestial body of the solar system. Javadoc The classes for bodies description are available in the package bodies of Patrius. Library Javadoc Orekit Package fr.cnes.sirius.patrius.bodies Patrius Package fr.cnes.sirius.patrius.bodies Links Orekit bodies : Orekit Bodies architecture description IAU report : Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009 Useful Documents None as of now. Package Overview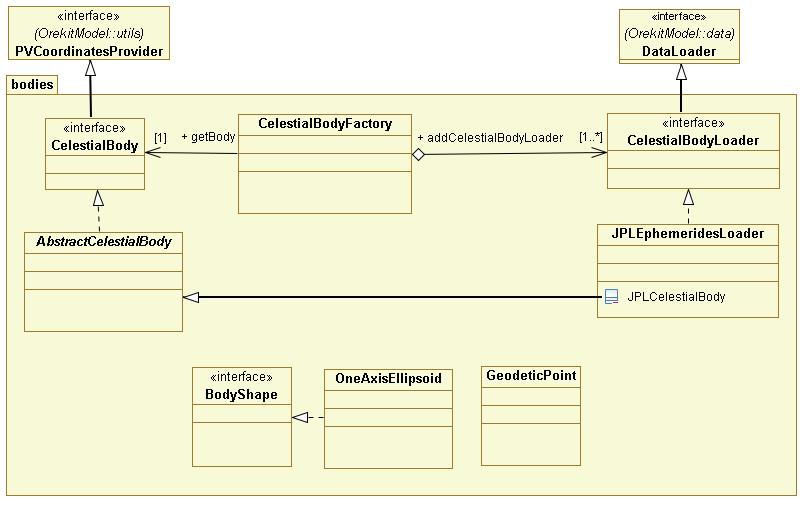 This package overview is from the OREKIT website, under apache license. Features Description Celestial bodies The Moon, the Sun and planets of the solar system are all represented by the CelestialBody interface. This class associates a name (eg Sun) to : a gravitational coefficient GM a body centered inertial frame (which can be retrieved with method getInertiallyOrientedFrame()). a body centered rotating frame (which can be retrieved with method getBodyOrientedFrame()). Inertially-oriented and body-oriented frames are defined in the following way: 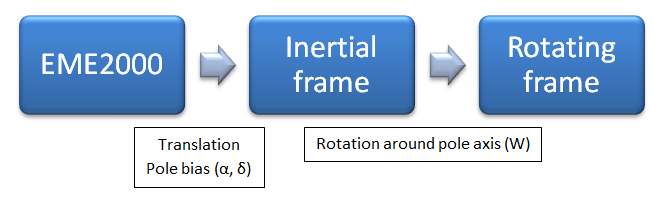Body-centered inertial frame is centered on the celestial body centered and pole axis (Z axis) is shifted by right ascension α and declination δ. Body-centered rotating frame is linked to inertially-oriented frame by a rotation of angle W(t) (reference values for W(t) is provided by IAU). To build a celestial body, the user can: use the static methods of the CelestialBodyFactory to create instances of the most common celestial bodies (Moon, Sun, Jupiter, etc.). JPL Ephemeris data are used. Warning: using the factory requires to load JPL Ephemeris data beforehand. use the simplified models (Meeus, etc.). creates its own celestial body using the class UserDefinedCelestialBody These methods are detailed in the following sections. Ephemeris Loader For any celestial body of the Solar System, the actual computation of its position and velocity relies on the JPL planetary ephemerides files. These files are binary files and loaded thanks to the JPLEphemeridesLoader object. For the moment, this object is only able to load the DE 405 or the DE 406 files which are the most commonly used data files. The former covers the years 1600 to 2200 at maximum precision, the latter covers the years-3000 to +3000 at only slightly reduced precision. The DE 421 file which is the latest JPL ephemeris with fully consistent treatment of planetary and lunar laser ranging data (Folkner et al 2009) is not yet readable by JPLEphemeridesLoader. However the DE 405 file is the basis for the Astronomical Almanac and leads to sufficiently accurate results and, for most purposes, even the accuracy of DE 406 is sufficient. JPLEphemeridesLoader In order to generate the ephemerides of one celestial body of the Solar System, one has to use the JPLEphemeridesLoader as follows :   final JPLEphemeridesLoader loaderEMB = new JPLEphemeridesLoader(fileName, JPLEphemeridesLoader.EphemerisType.EARTH_MOON); final JPLEphemeridesLoader loaderSSB = new JPLEphemeridesLoader(fileName, JPLEphemeridesLoader.EphemerisType.SOLAR_SYSTEM_BARYCENTER); CelestialBodyFactory.addCelestialBodyLoader(CelestialBodyFactory.EARTH_MOON, loaderEMB); CelestialBodyFactory.addCelestialBodyLoader(CelestialBodyFactory.SOLAR_SYSTEM_BARYCENTER, loaderSSB);   // Reference frame Frame icrf = FramesFactory.getICRF();   // Ephemeris of the Sun JPLEphemeridesLoader loader = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.SUN);   // Creation of the Sun CelestialBody sun = loader.loadCelestialBody(CelestialBodyFactory.SUN);   // Coordinates of the Sun given a date and a reference frame PVCoordinates pvSun = sun.getPVCoordinates(date, icrf); When the user wants to create a JPLEphemeridesLoader, first of all, he must supply the folder where the DE 405 and DE 406 files are stored. Then he has to give the name of the file which contains the data (DE 405 or DE 406), the type of celestial body and a date (desired central date) as entries of the JPLEphemeridesLoader. The first argument (name of the data file) may be null. In this case, Patrius takes the first compatible file found. If one wants only files from the DE 405 ephemerides, for instance, he has to give the String "^unx[mp](\\d\\d\\d\\d)\\.(?:405)$". The last argument can also be null. If the central date is not mentionned an arbitrary 100 days range will be loaded whereas if it is mentionned all data within a +/-50 days range around this date will be loaded. Once the data is loaded, thanks to the JPLEphemeridesLoader, the user can create the celestial body with the method loadCelestialBody() of the JPLEphemeridesLoader class. To do so, the user has to be sure that all required data is loaded. Indeed, apart from the Moon, the Earth and the Earth-Moon barycenter, the creation of a celestial body requires some data on the Earth Moon barycenter and the Solar System barycenter in order to instanciate the frame in which the ephemerides of the celestial body will be defined. Therefore, the user has to create a JPLEphemeridesLoader for the Earth-Moon barycenter and the Solar System barycenter prior to creating the celestial body, otherwise Patrius will arbitrarily load a DE file to generate the corresponding ephemerides that are used afterwards for the generation of the frame. Then the user has to complete the list of the loaders of the CelestialBodyFactory with these two loaders before calling the method loadCelestialBody(). NB : The user has to clean the CelestialBodyFactory memory if he does not want to work with the previously defined celestial bodies. JPL ephemerides The JPL ephemerides data is available on the JPL FTP server [R3]. Available ephemerides : Development Ephemerides Created in... Description DE102 September 1981 includes nutations but not librations. Referred to the dynamical equator and equinox of 1950. Covers JED 1206160.5 (-1410 APR 16) to JED 2817872.5 (3002 DEC 22) DE200 September 1981 includes nutations but not librations. Referred to the dynamical equator and equinox of 2000. Covers JED 2305424.7 (1599 DEC 09) to JED 2513360.5 (2169 MAR 31). This ephemeris was used for the Astronomical Almanac from 1984 to 2003. (See Standish, 1982 and Standish, 1990). DE202 October 1987 includes nutations and librations. Referred to the dynamical equator and equinox of 2000. Covers JED 2414992.5 (1899 DEC 04) to JED 2469808.5 (2050 JAN 02). DE403 May 1993 includes nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 2305200.5 (1599 APR 29) to JED 2524400.5 (2199 JUN 22). Fit to planetary and lunar laser ranging data.(See Folkner et al. 1994). DE405, DE406 May 1997 For the DE405: includes both nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 2305424.70 (1599 DEC 09) to JED 2525008.50 (2201 FEB 20) For the DE406 : the same as the DE405 except the time span : Spans JED 0624976.50 (-3001 FEB 04) to 2816912.50 (+3000 MAY 06) This is the same integration as DE405, with the accuracy of the interpolating polynomials has been lessened to reduce file size for the longer time span covered by the file. DE410 April 2003 includes nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 2415056.5 (1900 FEB 06) to JED 2458832.5 (2019 DEC 15). Ephemeris used for Mars Exploration Rover navigation. DE413 November 2004 includes nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 2414992.5, (1899 DEC 04) to JED 2469872.5 (2050 MAR 07). Created to update the orbit of Pluto to aid in planning for an occultation of a relatively bright star by Charon on 11 July 2005. DE414 May 2005 includes nutations and librations. Covers JED 2414992.5, (1899 DEC 04) to JED 2469872.5 (2050 MAR 07). Fit to ranging data from MGS and Odyssey through 2003. (See Konopliv et al., 2006.) DE418 August 2007 includes nutations and librations. Covers JED 2414864.7 (1899 JUL 29) to JED 2470192.5 (2051 JAN 21) DE421 February 2008 includes nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 2414864.7 (1899 JUL 29) to JED 2471184.7 (2053 OCT 09) Fit to planetary and lunar laser ranging data. (See Folkner et al., 2009) DE422 September 2009 includes nutations and librations. Referred to the International Celestial Reference Frame. Covers JED 625648.5, (-3000 DEC 07) to JED 2816816.5, (3000 JAN 30). Intended for the MESSENGER mission to Mercury. Extended integration time to serve as successor to DE406. Fit to ranging data from MGS and Odyssey through 2003. (See Konopliv et al., 2010.) DE423 February 2010 includes nutations and librations. Referred to the International Celestial Reference Frame version 2.0. Covers JED 2378480.5, (1799 DEC 16) to JED 2524624.7, (2200 FEB 02). Intended for the MESSENGER mission to Mercury. Simplified analytical models Meeus Model The Meeus Model is a simplified model which gives the position of the Sun and the Moon with respect to the time T expressed in centuries (TT time scale). This model is an analytical model less precise than the DE ephemerides given by JPL. It is adapted for onboard applications. The class implementing the Meeus Model allows three different models computing the position of the Sun with appropriate equations : the standard model (provided by Jean Meeus), the Stela model and an onboard model. The main differences between these model is the computation of the obliquity of the ecliptic : indeed, its value is fixed to 0 for the standard model, given by an expression involving [math]T, T^{2}[/math]for Stela model and [math]T, T^{2}, T^{3}[/math] for the onboard model. Moreover, the onboard model computed the position in J2000 frame, whereas standard and Stela models use respectively EOD and MOD frame. Regarding the precision, one has to expect a maximum difference of 25593km in position for the Sun and a maximum angular difference of 34.7 (wrt DE405 ephemerides). For the Moon, one has to expect a maximum difference of 26 km in position and a maximum angular difference of 15.2 (wrt DE405 ephemerides). As for the performances (in terms of execution time), the Meeus model for the Sun is faster than the DE405 ephemerides. However, we did not come to the same conclusion for the Moon even by decreasing the degree of precision (number of terms taken into account to compute the latitude, longitude and distance which are needed to compute in fine the position of the Moon). Deviation in position wrt DE423 Angular deviation wrt DE423 Sun 12000 km 34.7 Moon 62x66x46 12.4 km 15.2 Moon 26x13x13 225 km 122 Moon 9x4x3 1591 km 889 Deviation in position wrt DE405 Angular deviation wrt DE405 Sun 25593km 34.7 Moon 62x66x46 26 km 15.2 Number of elementary operations Number of trigonometric operations Sun 89 10 Moon 62x66x46 2671 182 Moon 26x13x13 917 60 Moon 9x4x3 401 24 References for the tables : "Modèles d'éphémérides luni-solaires", CNES DCT/SB/MS, 03/14/2011 "Modèle MEEUS pour éphémérides Lune-Soleil : Compléments sur le nombre d'opérations", CNES DCT/SB/MS execution time - DE405 execution time- MEEUS Sun 59 s 548 ms 19 s 938 ms Moon 62x66x46 11 s 625 ms 3 mn 22 s 323 ms Moon 26x13x13 11 s 625 ms 1 mn 17 s 74 ms Moon 9x4x3 11 s 625 ms 40 s 326 ms In order to build such a Sun or Moon, one has to use the object MeeusSun or MeeusMoon which both extend AbstractCelestialBody. Note that it is not possible to build those celestial bodies from the CelestialBodyFactory, for the moment. Basic board Sun model The basic board Sun model is a simplified analytical model which gives the direction of the Sun (the normalized position) with respect to time. This model is similar to the Meeus model (the constants of the model are different) and is adapted for onboard applications. The reference inertial frame is the CIRF. User-defined celestial bodies User can defined its own celestial body by using UserDefinedCelestialBody. This class requires to provide: Its name. Its position-velocity through time using a PVCoordinateProvider implementation. Its gravitational constant. Its pole motion using IAUPole implementation. Example: building Ceres. According to [FDY_BODY_Links IAU report], Ceres has the following parameters: α = 291◦ ± 5◦ δ = 59◦ ± 5◦ W = 170.90◦ + 952.1532◦d With d being the interval in days from the standard epoch (the standard epoch is JD 2451545.0, i.e. 2000 January 1 12 hours TDB) Ceres gravitational constant is 6.263E10 m^^3^^kg^^-1^^s^^-2^^. If one knows Ceres motion given for instance by a PVCoordinatePropagator pv, then one can build Ceres with the following code: // Gravitational parameter final double gm = 6.263E10;   // Pole motion final IAUPole pole = new IAUPole() { @Override public double getPrimeMeridianAngle(final AbsoluteDate date) { // W final double d = date.durationFrom(AbsoluteDate.J2000_EPOCH) / Constants.JULIAN_DAY; return FastMath.toRadians(170.90) + FastMath.toRadians(952.1532)* d; }   @Override public Vector3D getPole(final AbsoluteDate date) { // Pole bias: alpha and delta return new Vector3D(FastMath.toRadians(291), FastMath.toRadians(59)); } };   // Build Ceres body final CelestialBody ceres = new UserDefinedCelestialBody("Ceres", pv, gm, pole); Then ceres object possesses all features of: A CelestialBody: retrieve body-centered inertial frame or body-centered rotating frame A PVCoordinateProvider: retrieve position and velocity at any time Body shapes The one-axis ellipsoid is a good approximate model for most planet-size and larger natural bodies. It is the equilibrium shape reached by a fluid body under its own gravity field when it rotates. The symmetry axis is the rotation or polar axis. OneAxisEllipsoid This type is used to represent the shape of a planet. One very useful implementation represents an ellipsoid (OneAxisEllipsoid). It is constructed from an equatorial radius, a flattening coefficient, and a reference frame that will be used to localize Geodetic points on the shape. It could be interesting to obtained the geodetic coordinates of the nadir point of the satellite. To that purpose, one can use the method getIntersectionPoint(Line, Vector3D, Frame, AbsoluteDate) of the object OneAxisEllipsoid.   AbsoluteDate date = new AbsoluteDate(new DateComponents(2008, 03, 21), TimeComponents.H12, TimeScalesFactory.getUTC()); Frame frame = FramesFactory.getITRF(); // Body shape model OneAxisEllipsoid earth = new OneAxisEllipsoid(6378136.460, 1 / 298.257222101, frame);   // Satellite on any position   circ = new CircularOrbit(7178000.0, 0.5e-4, 0., FastMath.toRadians(50.), FastMath.toRadians(0.), FastMath.toRadians(90.), PositionAngle.MEAN, FramesFactory.getEME2000(), date, mu);   // Transform satellite position to position/velocity parameters in EME2000 and ITRF200B PVCoordinates pvSatEME2000 = circ.getPVCoordinates(); PVCoordinates pvSatItrf = frame.getTransformTo(FramesFactory.getEME2000(), date).transformPVCoordinates(pvSatEME2000); Vector3D pSatItrf = pvSatItrf.getPosition();   // Nadir point of the satellite Vector3D pointItrf = new Vector3D.ZERO; Vector3D direction = Vector3D(1., pSatItrf,-1., pointItrf); Line line = new Line(pSatItrf, direction); // intersection point between the ellipsoid and the line that joins the satellite and the center of the body GeodeticPoint nadir = earth.getIntersectionPoint(line, pSatItrf, frame, date); GeometricBodyShape and ExtendedOneAxisEllipsoid The GeometricBodyShape interface extends BodyShape for more complex computations. ExtendedOneAxisEllipsoid implements it. See the [MIS_SENSORS_PatriusBodySpheroid specific page] for more details. Facet celestial body FacetCelestialBody is a class used to define a celestial body as a mesh. This is particularly useful for small irregular bodies such as asteroids. For example, Phobos contains here 100 000 vertices and 200 000 facets: This class: Inherits the GeometricBodyShape interface and hence can be used together with EclipseDetector and SensorModel. Inherits the CelestialBody interface and hence can be used as any celestial bodies with classes such as ThirdBodyAttraction, SunPointing and event detectors. Provides some useful and optimised methods for small body handling. Facets are connected to each other allowing some methods to be writen in a recursive or iterative way and hence being very fast. If n is the number of vertices of the body, fast recursive or iterative methods are in O(log(n)). Mesh provider A mesh is described by a list of facets Triangle and or vertices Vertex. A Triangle contains three vertices. Mesh is provided by the generic interface MeshProvider. This interface currently possesses two implementation: ObjMeshLoader: in this case, the mesh is provided under official .obj file format. See This page for more information on the format. GeodeticMeshLoader: in this case, the mesh is provided in an ASCII column file listing each vertex in the format [Latitude Longitude Altitude]. Available methods Noe that most methods return exact results. For example, distanceTo methods returns exact distance to mesh body. Only transform() and getLocalRadius() methods simplify the mesh in a one axis ellipsoid. FacetCelestialBody provides the following methods: getIntersection(final Line line, final Vector3D close, final Frame frame, final AbsoluteDate date) and similar which returns an Intersection object.This object contains the intersection point as well as the Triangle containing the intersection point. This method is recursive and is in O(log(n)). transform() methods which converts a point or a geodetic point using reference ellipsoid. Reference ellipsoid is the closest one axis ellipsoid to the body. getLocalRadius() methods which provides the local radius from an object and an occulted body using reference ellipsoid. Reference ellipsoid is the closest one axis ellipsoid to the body. This method is to be used only by EclipseDetector. distanceTo() method which returns the distance to the body. This method is recursive and is hence in O(log(n)). getNeighbors() methods which returns the neighbors triangles to: A point or a triangle given a "neighborhood distance" A triangle given a "neighborhood order". In this case, order 1 returns the immediate neighbors of the triangles, order 2 returns also the neighbors' neighbors and so on. This method is recursive and is hence in O(log(n)). getSurfacePointedDataEphemeris() method which returns for each provided SpacecraftState a container SurfacePointedData, containing all pointed surface-related data. getFieldData() which returns a container FieldData containing data related to the field of view: Visible triangles from the satellite field of view IFieldOfView. A visible triangle must be entirely in the field of view and not masked by any other triangle. Contour of the seen triangles. Contour is strictly contained in the field of view If main direction of the field of view is provided, this method is recursive and is in O(log(n)). Otherwise, it is in O(n) and is much slower. isInEclipse() method which returns true if the satellite is currently in eclipse, false otherwise. Penumbra is not taken into account. This method is in O(log(n)). getNeverVisibleTriangles() which returns a list of facets which are never visible from the provided ephemeris. Visibility criteria is the same as for getFieldData() method. This method is in O((n)). getNeverEnlightenedTriangles() which returns a list of facets which are never enlightened by the Sun. Visibility criteria is the same as for getFieldData() method. This method is in O((n)). getVisibleAndEnlightenedTriangles() which returns a list of facets which are visible and enlightened at the same time, at least once on the provided ephemeris. Visibility criteria is the same as for getFieldData() method. This method is in O((n)). GeodeticPoint The geodetic point is defined by a latitude, a longitude and an altitude in the frame associated to the body. It could be interesting to know the position of a satellite in terms of geodetic coordinates rather than Cartesian ones and vice versa (the corresponding methods in OneAxisEllipsoid). // equatorial radius of the celestial body double ae = 6378137.0; // flatness of the celestial body double f = 1.0 / 298.257222101; // date AbsoluteDate date = AbsoluteDate.J2000_EPOCH; // reference frame attached to the body Frame frame = FramesFactory.getITRF(); // body shape model (ellipsoid) OneAxisEllipsoid model = new OneAxisEllipsoid(ae, f, frame);   // transformation with jacobian matrix : cartesian to geodetic   // initial cartesian point that will be transformed Vector3D cp = new Vector3D(4637885.347, 121344.708, 4362452.869); // coresponding geodetic point GeodeticPoint gp = model.transform(cp, frame, date);   // transformation with jacobian matrix : geodetic to cartesian   // initial geodetic point that will be transformed GeodeticPoint gp2 = new GeodeticPoint(0.852479154923577, 0.0423149994747243, 111.6); // coresponding Cartesian point Vector3D cp2 = model.transform(gp2); It could be also interesting to obtain the jacobian matrix of the transformation. // transformation : cartesian to geodetic   double[][] jacobianGeodesicWrtCartesian = new double[3][3]; gp = model.transformAndComputeJacobian(cp, frame, date, jacobianGeodesicWrtCartesian);   // transformation : geodetic to cartesian   double[][] jacobianCartesianWrtGeodesic = new double[3][3]; Vector3D cp2 = model.transformAndComputeJacobian(gp2, jacobianCartesianWrtGeodesic ); Getting Started TBD Contents Interfaces Interface Summary Javadoc BodyShape Interface representing the rigid surface shape of a natural body. ... CelestialBody Interface for celestial bodies like Sun, Moon or solar system planets. ... MeshLoader Interface for FacetCelestialBody mesh provider. ... Classes Class Summary Javadoc CelestialBodyFactory Factory class for bodies of the solar system. ... GeodeticPoint Point location relative to a 2D body surface. ... JPLEphemeridesLoader Loader for JPL ephemerides binary files (DE 405, DE 406, ...). ... OneAxisEllipsoid Modeling of a one-axis ellipsoid. ... MeeusSun Position of the Sun according to Meeus model. Three models with there appropriate equations are avaible : the standard model (former MeeusSun), Stela model (former MeeuSunStela) and an on-board model ... MeeusMoon Position of the Moon according to Meeus model. ... BasicBoardSun Direction of the Sun according to a basic board Sun model. ... UserCelestialBody User-defined celestial body ... FacetCelestialBody Celestial body defined by a mesh. ... Triangle Unitary facet (triangle) for a FacetCelestialBody. ... ObjMeshLoader .obj 3D file mesh loader. ... GeodeticMeshLoader Mesh loader for ASCII files describing the body with latitude/longitude/altitude components (1 per line). ... irius/patrius/math/transform/AbstractFastFourierTransformer.html ...]
FastFourierTransformer	Computes the FFT for real and complex arrays.	...