User Manual 3.3 Events: orbital
Introduction
Scope
Here are presented all the events detectors of the theme "orbit determination".
Javadoc
Those event detectors are available in the packages :
|=Library|=Javadoc
|Orekit |Package org.orekit.propagation.event
|Patrius |Package fr.cnes.sirius.patrius.events
Features Description
Detectors
This section describes the meaning of the g switching function for the "orbit determination" event detectors, and their particularities :
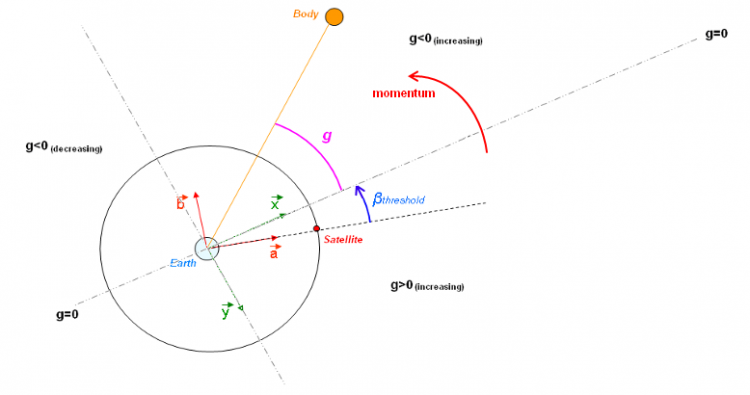
Alignment Detector
This detector computes the difference [math]\displaystyle{ \theta }[/math] between the alignment angle [math]\displaystyle{ \beta_{threshold} }[/math] and the angle between the satellite position, the central body and the second body position projection in the orbital plane.
If [math]\displaystyle{ \theta_1 =-\pi - \theta }[/math] and [math]\displaystyle{ \theta_2 = \pi - \theta }[/math], the g switching function will be:
[math]\displaystyle{ \theta_1 }[/math] if [math]\displaystyle{ \theta \lt \theta_1 }[/math],
[math]\displaystyle{ \theta }[/math] if [math]\displaystyle{ \theta \lt \theta_2 }[/math],
and [math]\displaystyle{ \theta_2 }[/math] otherwise.
[math]\displaystyle{ \beta_{threshold} }[/math] is an oriented angle and is positive when is oriented as the orbital momentum.
Axes [math]\displaystyle{ \vec a }[/math] (satellite normalized position) and [math]\displaystyle{ \vec b }[/math] (satellite normalized velocity) are transformed into axes [math]\displaystyle{ \vec x }[/math] and [math]\displaystyle{ \vec y }[/math] knowing the value of [math]\displaystyle{ \beta_{threshold} }[/math] angle; g is found projecting the target body position in the orbital plane and computing its [math]\displaystyle{ \vec x }[/math] and [math]\displaystyle{ \vec y }[/math] components.
- [math]\displaystyle{ g\gt 0 : }[/math] target body projection is in the half-plane [math]\displaystyle{ y\gt 0 }[/math]
- [math]\displaystyle{ g\lt 0 : }[/math] target body projection is in the half-plane [math]\displaystyle{ y\lt 0 }[/math]
- [math]\displaystyle{ g=0 : }[/math] target body projection belongs to the straight line [math]\displaystyle{ y=0 }[/math]
Altitude Detector
The g switching function measures the difference between the current altitude [math]\displaystyle{ h_{sat} }[/math] and the threshold altitude [math]\displaystyle{ h_{thr} }[/math].
- [math]\displaystyle{ g \gt 0 : h_{sat} \gt h_{thr} }[/math]
- [math]\displaystyle{ g\lt 0 : h_{sat} \lt h_{thr} }[/math]
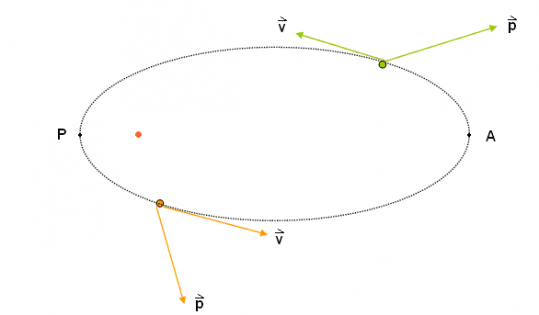
ApsideDetector
The g switching function is the dot product of the satellite position and velocity vectors: [math]\displaystyle{ g =\vec p \cdot \vec v }[/math]
- [math]\displaystyle{ g\gt 0 : }[/math] the satellite is in the half-orbit from perigee to apogee;
- [math]\displaystyle{ g\lt 0 : }[/math] the satellite is in the half-orbit from apogee to perigee.
DateDetector
The g switching function is the value of the difference between the current date and the target date. If no event dates have been added i.e. if no target dates have been initialized, [math]\displaystyle{ g=-1 }[/math].
EclipseDetector
This detector is in charge of the umbra/penumbra eclipse events detection. Different features are available:
- the occulted and occulting bodies are both spherical;
- the occulted body is a direction;
- the occulting body has an ellipsoid shape.
In addition to that, the EclipseDetector can detect eclipse events based on a threshold lighting ratio [math]\displaystyle{ \epsilon_{0} }[/math]:
[math]\displaystyle{ 0\lt =\epsilon_{0}\lt =1 }[/math].
When [math]\displaystyle{ \epsilon_{0}=0 }[/math], an eclipse event is triggered only if whole occulted body is hidden by the occulting body (total eclipse); when [math]\displaystyle{ \epsilon_{0}=1 }[/math], an event is immediately triggered when the occulted body is partially hidden (penumbra eclipse).
As a general rule, the lighting ratio is equal to:
[math]\displaystyle{ \epsilon = 1-\frac{A_{occulted}}{\pi r_{occulted}^2} }[/math]
where [math]\displaystyle{ r_{occulted} }[/math] is the apparent radius of the occulted body.
The g function is: [math]\displaystyle{ g=\epsilon_{0}-\epsilon }[/math]
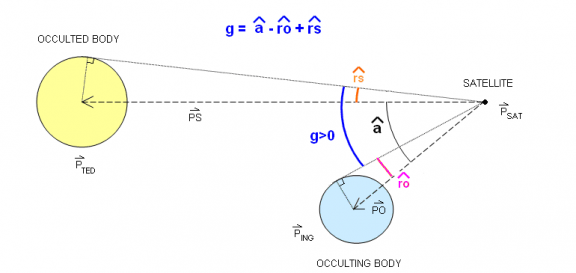
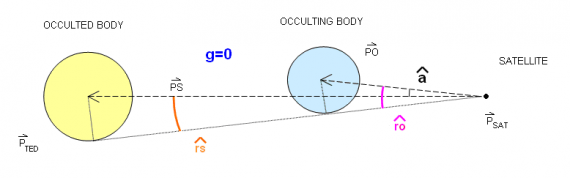
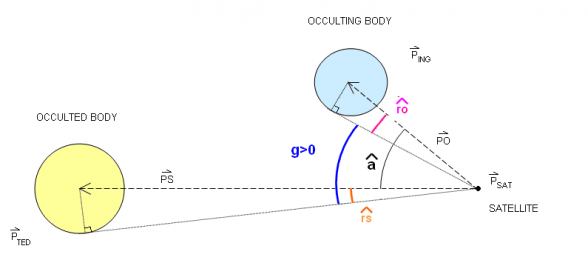
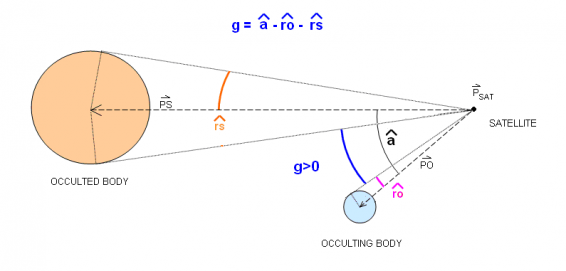
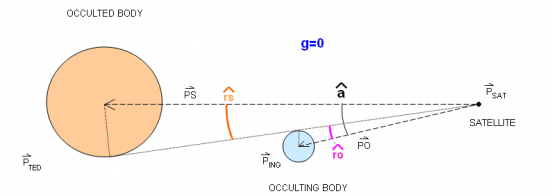
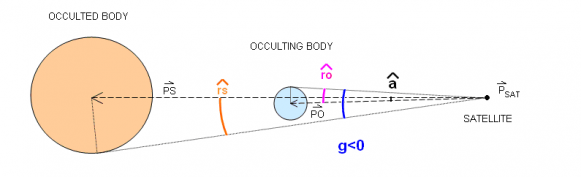
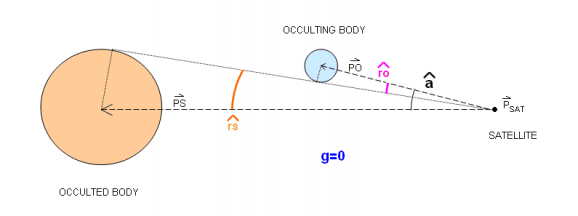
The g switching function computation needs the satellite position vector ([math]\displaystyle{ \vec P_{sat} }[/math]), the occulted body ([math]\displaystyle{ \vec P_{ted} }[/math]) and occulting body ([math]\displaystyle{ \vec P_{ing} }[/math]) position vectors. [math]\displaystyle{ \vec {PS}=\vec {P_{ted}}-\vec {P_{sat}} }[/math], [math]\displaystyle{ sin(\widehat{rs})=\dfrac{r_{ted}}{|\vec {PS}|} }[/math] [math]\displaystyle{ \vec {PO}=\vec {P_{ing}}-\vec {P_{sat}} }[/math], [math]\displaystyle{ sin(\widehat{ro})=\dfrac{r_{ing}}{|\vec {PO}|} }[/math]. [math]\displaystyle{ \alpha }[/math] is the angle between [math]\displaystyle{ \vec {PS} }[/math] and [math]\displaystyle{ \vec {PO} }[/math]. Distinction is made between total eclipse and partial eclipse. The following diagrams show the evolution of the g function value for an eclipse scenario with two spherical bodies.
Total eclipse
The passage to umbra is detected. The g switching function is [math]\displaystyle{ g = \alpha- \widehat{ro} + \widehat{rs} }[/math].
- [math]\displaystyle{ g\gt 0 : }[/math] satellite is not in eclipse:
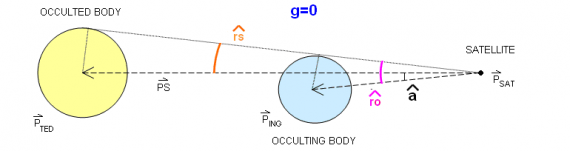
- [math]\displaystyle{ g=0 : }[/math] beginning of umbra:
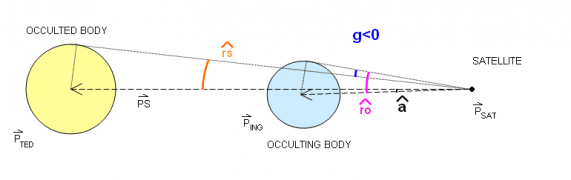
- [math]\displaystyle{ g\lt 0 : }[/math] umbra:
- [math]\displaystyle{ g=0 : }[/math] end of umbra:
- [math]\displaystyle{ g\gt 0 : }[/math] satellite is not in eclipse:
Partial eclipse
The passage to penumbra is detected. The g switching function is [math]\displaystyle{ g = \alpha- \widehat {ro} - \widehat {rs} }[/math].
- [math]\displaystyle{ g\gt 0 : }[/math] satellite is not in eclipse:
- [math]\displaystyle{ g=0 : }[/math] beginning of penumbra:
- [math]\displaystyle{ g\lt 0 : }[/math] penumbra:
- [math]\displaystyle{ g=0 : }[/math] end of penumbra:
Another feature of the EclipseDetector is the detection of partial and total eclipse by a spheroid.
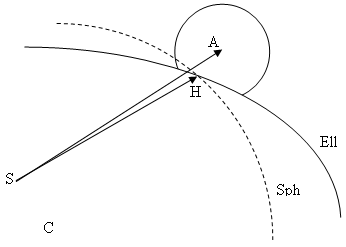
The point on the horizon (H) is calculated as the point of the ellipsoid that is in the same plane as A, C and S (respectively center of occulted body, center of occulting body and satellite). The distance of H to the center C of the ellipsoid is then projected onto a plane orthogonal to the Satellite / Occulting (SA) body direction, and the resulting length is considered as the radius of an "apparent" sphere representing the occulting body. The partial and total eclipse are then computed as per above.
Particular case
A specific case is having a spacecraft lower than the occulting body radius (i.e. spacecraft altitude < occulting body radius). Two cases are possible:
- The satellite is behind the occulted body (angle occulted body- occulting body - satellite > Pi/2): satellite is considered to be in total eclipse.
- The satellite is in front of the occulted body (angle occulted body- occulting body - satellite <= Pi/2): apparent radius of occulting body cannot be computed. Hence it is considered to be equal to Pi/2 (slight approximation since it means satellite is considered to be lying exactly on the surface of the occulting body). Then usual computation of g function applies.
NodeDetector
The NodeDetector detects the orbital nodes; the user can choose what the detect (ascending nodes, descending nodes or both) through the slopeSelection parameter.
The g switching function returns the Z component of the satellite position in the geocentric frame:
- [math]\displaystyle{ g\gt 0 : }[/math]the satellite is over the equatorial plane (in its orbit from ascending node to descending node);
- [math]\displaystyle{ g\lt 0 : }[/math]the satellite is under the equatorial plane (in its orbit from descending node to ascending node);
DistanceDetector
The DistanceDetector detects the time when the distance between the spacecraft and a point of space reaches a given value.
The point of space is given as a PVcoordinatesProvider : it can be either a celestial body (as a CelestialBody), a point at the surface of a body (as a TopocentricFrame), or any another class that implements that interface.
Here is the example for a point on the surface of a body :
// earth shape
final BodyShape earth = new OneAxisEllipsoid(earthRadius, ea, ITRFFrame);
// considered point
final GeodeticPoint point = new GeodeticPoint(latitude, longitude, altitude);
// associated topocentric frame : this object is a PVCoordinatesProvider
final TopocentricFrame topoFramePoint = new TopocentricFrame(earth, point, "Gstation");
// detector
final DistanceDetector detector = new DistanceDetector(topoFramePoint, distance);
Its g switching function computes the difference between the spacecraft position and the point position (in the same frame), and then subtracts the given distance from its norm.
- [math]\displaystyle{ g\gt 0 : }[/math]the distance spacecraft/point is bigger than the distance threshold value;
- [math]\displaystyle{ g\lt 0 : }[/math]the distance spacecraft/point is smaller than the distance threshold value;
ExtremaDistanceDetector
The ExtremaDistanceDetector detects if the spacecraft is at a local extremum for the distance relative to a point of space, defined the same way as in the previous DistanceDetector. The choice of the extremum (maximum, minimum, or both) is done with the constructor, through the distanceType parameter.
The g switching function returns the square norm of the velocity for the vector representing this distance, thus the sign change is indeed a local extremum.
ExtremaLatitudeDetector
The ExtremaLatitudeDetector detects if the spacecraft is at a local extremum for the geodetic latitude. The choice of the extremum (maximum, minimum, or both) is done with the constructor, through the latitudeType parameter.
The g switching function returns the z-component of the spacecraft velocity in the orbit definition frame.
LatitudeDetector
The LatitudeDetector detects the time when the spacecraft reaches a given geodetic latitude, the BodyShape of the earth being known to compute it.
The g switching function returns the difference between the current latitude and the one to detect.
ExtremaLongitudeDetector
The ExtremaLongitudeDetector detects if the spacecraft is at a local extremum for the longitude. The choice of the extremum (maximum, minimum, or both) is done with the constructor, through the extremumType parameter.
The g switching function is the dot vector of the position with the result of the cross product of the velocity relative to the body and unitary vector Z : [math]\displaystyle{ g =\vec P \cdot (\vec Vrel \wedge \vec Vz) }[/math]
The main part of this function is the cross product which switches when the relative velocity is colinear to Z.
LongitudeDetector
The LongitudeDetector detects the time when the spacecraft reaches a given longitude.
Working with longitude always gives a problem of continuity when longitude pass from PI rad to- PI rad. The best solution find to avoid this is to save some information from the last computation of the g function.
In this way the g function is the following difference expressed between-PI rad and PI rad : currentLongitude - longitudeToDetect
At each g function call, this difference is saved, and each time the difference between the current difference and the last difference is greater than PI rad, it means there is a discontinuity, the g fonction is opposed. This avoids discontinuity. Then all zero are detected.
This solution, also avoids problem about detecting a longitude at PI rad further (that we meet with a sin(a- b) g function).
AOLDetector
The AOLDetector detects when the spacecraft reaches a predetermined argument of latitude (true, mean or eccentric supportes) with respect to a given equator ; the argument of latitude is the angle between the spacecraft position and the ascending node.
The g switching function returns the sinus of the difference between the spacecraft current angular position [math]\displaystyle{ \beta }[/math] and the threshold position value [math]\displaystyle{ \beta_{input} }[/math]: [math]\displaystyle{ g=sin(\beta- \beta_{input}) }[/math] An AOL event is triggered only if the g-function slope is positive at its zero.
AnomalyDetector
The AnomalyDetector detects when the spacecraft reaches a predetermined anomaly; the anomaly is the angle between the spacecraft position and the perigee.
Three types of anomaly can be detected: true, mean and eccentric anomaly.
The g switching function returns the sinus of the difference between the spacecraft current anomaly and the threshold anomaly value:
[math]\displaystyle{ g=sin(\alpha- \alpha_{input}) }[/math]
(This g function is identical to the AOLDetector g function).
Like the AOLDetector, an anomaly event is triggered only if the g-function slope is positive at its zero.
Using precaution : This detector is unusable on a circular orbit where the perigee always moves very fast and in any way.
ThreeBodiesAngleDetector
The ThreeBodiesAngleDetector detects when the angle between three bodies (they can be celestial bodies, spacecrafts, ground stations, ...) is equal to a predetermined value.
If [math]\displaystyle{ \vec{P_{1}} }[/math], [math]\displaystyle{ \vec{P_{2}} }[/math] and [math]\displaystyle{ \vec{P_{3}} }[/math] are the positions of the three bodies, and [math]\displaystyle{ \vec{P_{21}} }[/math] is the difference [math]\displaystyle{ \vec{P_{2}}-\vec{P_{1}} }[/math] and [math]\displaystyle{ \vec{P_{23}} }[/math] the difference [math]\displaystyle{ \vec{P_{2}}-\vec{P_{3}} }[/math], the computed angle will be: [math]\displaystyle{ \widehat{\vec{P_{21}} \vec{P_{23}}} }[/math]
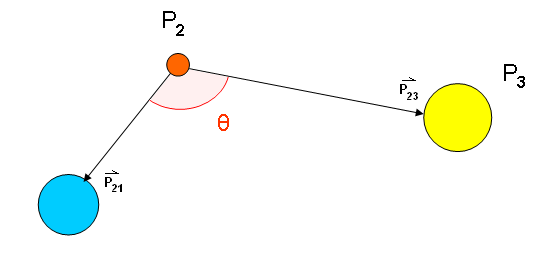
The g switching function returns the difference between the current angle between the three bodies and the threshold angle. The threshold angle is not oriented and its value is between 0 and PI.
ExtremaThreeBodiesAngleDetector
The ExtremaThreeBodiesAngleDetector detects when the angle between three bodies (defined the same way as in the ThreeBodiesAngleDetector) reaches its minimal or maximal value.
The choice of the detected extremum (maximum, minimum, or both) is done with the constructor, through the extremumType parameter.
The g switching function returns the derivative of the angle value (in fact, part of the derivative : a factor with a constant sign has been ignored). This derivative is obtained by expressing all the positions and velocities of the two extreme points ([math]\displaystyle{ P_{1} }[/math] and [math]\displaystyle{ P_{3} }[/math]) in a frame linked to the one at the angle origin ([math]\displaystyle{ P_{2} }[/math]). If the two vectors from the new origin are [math]\displaystyle{ \vec{P_{21}} }[/math] and [math]\displaystyle{ \vec{P_{23}} }[/math] the angle expression is : [math]\displaystyle{ \arccos(\vec{P_{21}}.\vec{P_{23}} / (|\vec{P_{21}}|.|\vec{P_{23}}|)) }[/math] Once derivated as [math]\displaystyle{ (gof)' = (g'of).f' }[/math] and the [math]\displaystyle{ arccos }[/math] derivative being always negative, the switching function is minus the derivative of the inner expression [math]\displaystyle{ \vec{P_{21}}.\vec{P_{23}} / (|\vec{P_{21}}|.|\vec{P_{23}}|) }[/math].
BetaAngleDetector
The BetaAngleDetector detects when the beta angle reaches a predetermined value; the beta angle is the angle between the orbit plane and the vector to the Sun.
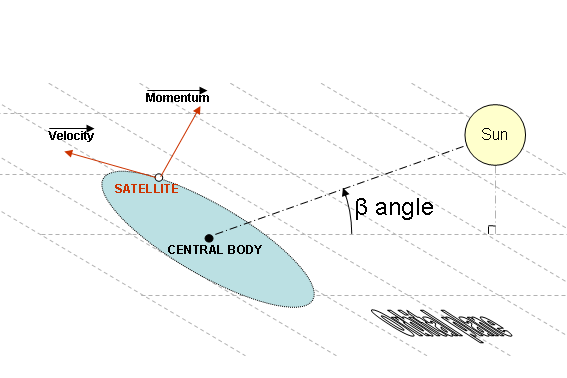
The beta angle belongs to [- π/2 , π/2 ]; its sign is positive when the Sun is in the half-plane containing the spacecraft's momentum.
LocalTimeDetector
The LocalTimeDetector detects when the spacecraft local time is equal to a predetermined value; the spacecraft local time is the angle between the projections of the Earth-Sun vector and the Earth-spacecraft vector in the equatorial plane. The local time angle is zero at 12.00h and is PI at 0.00h.
The local time is increasing for prograde orbits and decreasing for retrograde orbits. The events are detected in both cases.
The g function is the following difference expressed between-PI rad and PI rad : [math]\displaystyle{ currentLocalTime- localTimeToDetect }[/math]
At each g function call, this difference is saved, and each time the difference between the current difference and the last difference is greater than PI rad, it means there is a discontinuity, the g fonction is opposed. This avoids discontinuity. Then all zero are detected.
This solution, also avoids problem about detecting a local time at PI rad further (that we meet with a sin(a- b) g function).
SolarTimeDetector
The SolarTimeDetector detects when the spacecraft solar time is equal to a predetermined value; the spacecraft solar time is the angle between the the Earth-Sun projection in the orbital plane and the Earth-spacecraft vector. The solar time angle is zero at 12.00h and is PI at 0.00h.
The solar time is always increasing with time. It is mesured around the orbit momentum.
The g switching function returns the sinus of the difference between the spacecraft current solar time [math]\displaystyle{ \theta }[/math] and the threshold solar time value [math]\displaystyle{ \theta_{t} }[/math]:
[math]\displaystyle{ g=sin(\theta- \theta_{t}) }[/math]
Like the AOLDetector, a solar time event is triggered only if the g-function slope is positive at its zero.
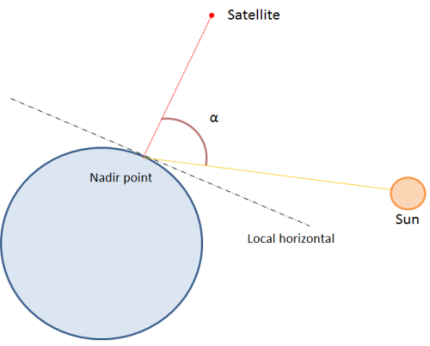
NadirSolarIncidenceDetector
The NadirSolarIncidenceDetector detects when the solar incidence, seen from the nadir point of the spacecraft, reaches a predetermined value.
The solar incidence is the angle between the nadir- satellite vector and the nadir - sun vector.
EarthZoneDetector
The EarthZoneDetector detects when the spacecraft enters and leaves an earth zone. Several separated zones can be defined for one detector instance. In that case, the EarthZoneDetector detects the entery of the satellite NADIR point in any of the zones.
The zones can be described two ways :
- As an array of {latitude, longitudes} that define the geodetic points with a zero altitude on a BodyShape. With this definition, the test made will be the entering of the spacecraft's NADIR point in the zone.
- As an array of vectors expressed in a given frame. With this definition, the entering of the spacecraft itself in the conic field from the center of the given frame to those points will be detected. Note that the given frame must be a terrestrial frame for the detection of earth zones entering, but the use of other frames is possible (other bodies, inertial frames…).
In both cases, the points must respect the following conditions :
- At least 3 points are needed to define a zone
- two consecutive points must not be too close (1.e-10 on the difference of thier normalized values)
- the arc between two consecutive points must not cross the one between two consecutive others of the same zone.
The points must also be given in the right order : from the point i to the point i + 1, if the associated vector from the center of the earth are [math]\displaystyle{ v_{i} }[/math] and [math]\displaystyle{ v_{i + 1} }[/math], the inside of the zone is on the left, e.g. the side of the positive cross vector [math]\displaystyle{ v_{i} . v_{i + 1} }[/math].
Constructors with default maxCheck and threshold values are available, but beware of their values, and use the other constructors if needed : if the zone is complex and the MaxCheck too large, the event detection could fail, because it would not manage to converge. To compute the event with enough precision to converge, set a small enough MaxCheck. To compute an approximative event even if the zone is precise and complex, set a large enough Threshold.
Particular detections
All those detectors can be used for the following particular cases :
- sub-solar point reaching : use the SolarTimeDetector with a "12h" time to detect.
- generic masking by a spherical body : use the GenericEclipseDetector, or the ThreeBodiesAngleDetector.
- terminator reaching (the nadir point reaches the night / day limit) : use the NadirSolarIncidenceDetector with a zero incidence.
- Sun interference in ground antennas : use the ThreeBodiesAngleDetector.
- RF interference between the main spacecraft and another one : use the ThreeBodiesAngleDetector
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
Interfaces
All the detectors implement the interface :
|=Interface|=Summary|=Javadoc | EventDetector|This interface represents an event finder.|EventDetector
Classes
|=Classe|=Summary|=Javadoc | AlignmentDetector|This class handles (satellite/central body/projection in the orbital plane of secondary body) alignment events.|AlignmentDetector | AltitudeDetector|This class handles satellite altitude crossing events.|AltitudeDetector | ApsideDetector|This class handles satellite apogee and perigee crossing events.|ApsideDetector | DateDetector|This class handles the occurrence of predefined dates.|DateDetector | EclipseDetector|This class handles total or partial eclipse events.|EclipseDetector | NodeDetector|This class handles satellite equator crossing events.|NodeDetector | DistanceDetector|This class handles events relating to the distance between the satellite and a given body.|DistanceDetector | ExtremaDistanceDetector|This class handles events representing the reaching of extrema for the distance to a given body.|ExtremaDistanceDetector | ExtremaLatitudeDetector|This class handles events representing the reaching of extrema for the geodetic latitude.|ExtremaLatitudeDetector | ExtremaLongitudeDetector|This class handles events representing the reaching of extrema for the longitude.|ExtremaLongitudeDetector | LatitudeDetector|This class handles events representing the reaching of a given geodetic latitude, the earth shape being known.|LatitudeDetector | LongitudeDetector|This class handles events representing the reaching of a given longitude|LongitudeDetector | AnomalyDetector|This class handles events representing the reaching of an anomaly angle.|AnomalyDetector | AOLDetector|This class handles events representing the reaching of an argument of latitude value.|AOLDetector | ThreeBodiesAngleDetector|This class handles events representing the reaching of a predetermined angle between three bodies.|ThreeBodiesAngleDetector | ExtremaThreeBodiesAngleDetector|This class handles events representing the reaching of of extrema for the angle between three bodies.|ExtremaThreeBodiesAngleDetector | BetaAngleDetector|This class handles the event : reaching a given beta angle value for a spacecraft.|BetaAngleDetector | LocalTimeDetector|This class handles events representing the reaching of a predetermined spacecraft local time.|LocalTimeDetector | SolarTimeDetector|This class handles events representing the reaching of a predetermined spacecraft solar time.|SolarTimeDetector | NadirSolarIncidenceDetector|This class handles events representing the reaching of a predetermined spacecraft nadir point solar incidence.|NadirSolarIncidenceDetector | EarthZoneDetector|This class handles events representing the entering and leaving of earth zones.|EarthZoneDetector
Tutorials
Tutorial 1
Modèle:SpecialInclusion prefix=$theme sub section="Tuto1"/
Tutorial 2
Modèle:SpecialInclusion prefix=$theme sub section="Tuto2"/