User Manual 4.9 Matrices

De Wiki
Révision de 6 mai 2022 à 07:36 par Admin (discussion | contributions) (Page créée avec « __NOTOC__ == Introduction == === Scope === This section will focus on the following aspects : * Matrix3D and Vector3D * Generic Matrices * UD Decomposition === Javadoc... »)

(diff) ← Version précédente | Voir la version courante (diff) | Version suivante → (diff)
Aller à : navigation, rechercher

Introduction

Scope

This section will focus on the following aspects :

  • Matrix3D and Vector3D
  • Generic Matrices
  • UD Decomposition

Javadoc

The relevant packages are documented here :

Library Javadoc
Patrius Package fr.cnes.sirius.patrius.math.linear
Patrius Package fr.cnes.sirius.patrius.math.geometry.euclidean.threed

Links

None as of now.

Useful Documents

None as of now.

Packages Overview

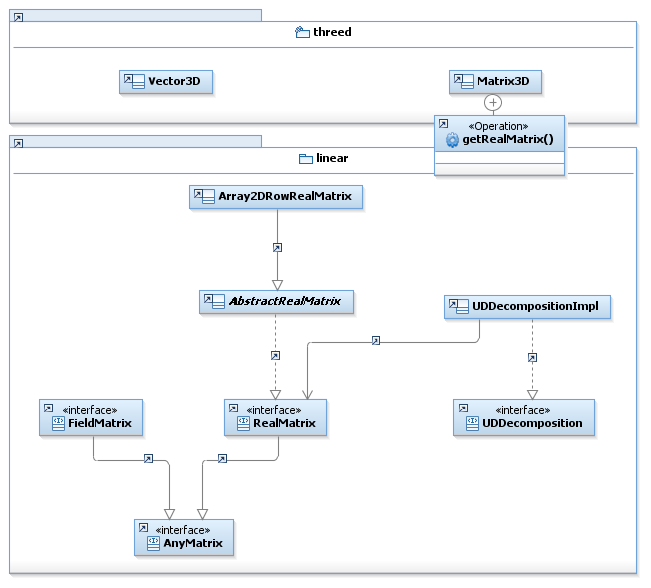
The matrices functionality can be found in the following packages :

  • fr.cnes.sirius.patrius.math.geometry.euclidean.threed for Vector3D, Matrix3D
  • fr.cnes.sirius.patrius.math.linear for RealMatrix, AbstractRealMatrix, Array2DRowRealMatrix, UDDecomposition, UDDecompositionImpl ...

PATRIMOINESIRIUSDiagrammeMUmatricesgeneriques.png

Features Description

The Matrix3D class

The Matrix3D is a real matrix designed to be used in geometric calculations. The Matrix3D is compatible with the Vector3D type, unlike the matrices implemented in the package "linear".

The packages "linear" and "geometry" both contains classes to represent vectors and matrices, but without any compatibility (for example, the "multiply" methods availables in the generic real matrices only accept the objects from the "linear" package).

To make possible the operations using both types of vectors and matrices, a constructor and a getter are added to the Vector3D and Matrix3D classes.


The constructor creates the object from a similar one (containing the same data) from the "linear" package.

For vectors : 

ArrayRealVector realVector = new ArrayRealVector(data);
Vector3D vector3D = new Vector3D(realVector);

For matrices, the operation is described in the previous paragraph.

This construction works only if the generic real vectors and matrices dimensions are right (3 for the vectors and 3x3 for the matrices).


The getters are : "getRealMatrix()" in the Matrix3D class and "getRealVector()" in the Vector3D class. They return the generic objects containing identical data.

Generic real matrices

The library also provides generic representations of real matrices, of any size.

The RealMatrix interface presents the following services :

  • usual operations (adding, multiplying)
  • extraction of submatrices
  • symmetry and antisymmetry tests
  • orthogonality tests
  • diagonality tests
  • invertibility tests

The Array2DRowRealMatrix is one available implementation for generic real matrices.

Decompositions

PATRIUS provides several ways for matrix decomposition. Interface for decomposition is Decomposition. A decomposition provides a way to:

  • Inverse a matrix
  • Separate a matrix into a product of specific matrices (orthogonal, upper triangular, etc.) depending on the solver type.

Standard decomposition in PATRIUS are:

  • QRDecomposition
  • LUDecomposition
  • CholeskyDecomposition
  • SingularValueDecomposition
  • UDDecompositionImpl

RealMatrix interface possesses a method to get its inverse. If not provided, by default a LUDecompositionis used.

Exemple with UD decomposition

The library can compute the UD decomposition of a matrix.

The UD-decomposition of the matrix A is a set of three matrices such that A = UxDxU^^t^^ with :

  • U is an upper triangular matrix,
  • D is a diagonal matrix,
  • U^^t^^ is the transpose of U.

Symmetric matrices

Symmetric matrices are handled through the generic SymmetricMatrix interface. An implementation is provided: ArrayRowSymmetricMatrix. This implementation optimally stores data in one single 1D-array.

Getting Started

Matrix3D and Vector3D

The Matrix3D class

A Matrix3D instance be constructed from doubles : 

double[][] data = { {1d,2d,3d}, {2d,5d,3d}, {1d,0d,8d} };
 
Matrix3D matrix3d = new Matrix3D(data);

Or from a RealMatrix : 

Array2DRowRealMatrix matrixCM = new Array2DRowRealMatrix(data);
 
Matrix3D matrix3D = new Matrix3D(matrixCM);

If the RealMatrix or data dimensions are not 3x3, a MathIllegalArgumentException is thrown.

Some basic methods are available in it :

  • Matrix3D / Matrix3D addition
Matrix3D matrix3d_result = matrix3d_1.add(matrix3d_2);
  • Matrix3D / Matrix3D subtraction
Matrix3D matrix3d_result = matrix3d_1.subtract(matrix3d_2);
  • Matrix3D / Matrix3D multiplication
Matrix3D matrix3d_result = matrix3d_1.multiply(matrix3d_2);
  • Matrix3D / Vector3D multiplication
Vector3D vector3d_result = matrix3d.multiply(vector3d);
  • Matrix3D / double multiplication
Matrix3D matrix3d_result = matrix3d.multiply(2.0);
  • transposition
Matrix3D transposed_matrix3d = matrix3d.transpose();
  • transposition and Matrix3D / Vector3D multiplication
Vector3D vector3d_result = matrix3d.transposeAndMultiply(vector3d);
  • test : orthogonal matrix ? Uses the same-named function in AbstractRealMatrix : same principle, same use.
  • getRealMatrix : returns an Array2dRowRealMatrix with the same data in it
RealMatrix realmatrix = matrix3d.getRealMatrix();
  • toString : creates a string containing all the values.

final Matrix3D matrix = new Matrix3D(testData);
returns "Matrix3D{{1.0,2.0,3.0},{2.0,5.0,3.0},{1.0,0.0,8.0}}"


Generic matrices

The AbstractRealMatrix class

Symmetry and antisymmetry tests

The RealMatrix interface and the AbstractRealMatrix abstract class contain the two methods isSymmetric and isAntisymmetric to test if a real matrix is symmetric or antisymmetric: 

Array2DRowRealMatrix sym = new Array2DRowRealMatrix(symmetricData);
 
boolean isSymmetric = sym.isSymmetric() ;

The returned boolean is TRUE if the matrix is symmetric. The equality test made on each value uses the MathUtils.equalsWithRelativeTolerance method, with an algorithm using a relative threshold described in the “Doubles Values Comparisons” paragraph of the SUM.


isAntisymmetric needs a threshold given by the user for the comparisons the zero of the diagonal values. This threshold can be taken as MathUtils.DOUBLES_COMPARISON_EPSILON for standard cases.

But if the matrix contains values closer to zero than this epsilon (1.0e-14), the user shall define their own threshold.

For the rest of the values tested (other than the diagonal), the same method as in isSymmetric is used. 

Array2DRowRealMatrix antisym = new Array2DRowRealMatrix(antisymmetricData);
 
boolean isAntisymmetric = antisym.isAntisymmetric(Precision.DOUBLE_COMPARISON_EPSILON) ;

The returned boolean is TRUE if the matrix is antisymmetric.


Orthogonal test

In order to know if a real matrix is orthogonal, one can use the method isOrthogonal(), this method checks if the column vectors form an orthonormal set : 

        double[][] orthogonalMatrix = {{ 8.0 / 9.0, 1.0 / 9.0,-4.0 / 9.0 },
                {-4.0 / 9.0, 4.0 / 9.0, -7.0 / 9.0 },
                { 1.0 / 9.0, 8.0 / 9.0, 4.0 / 9.0 }};
        RealMatrix matrix = new Array2DRowRealMatrix(orthogonalMatrix);
        matrix.isOrthogonal(Precision.EPSILON, Precision.EPSILON));

Of course, because a matrix usually results from several operations which can introduce numerical errors, one has to give 2 thresholds under which the matrix is considered to be orthogonal. These thresholds concern the normality and the orthogonality of the column vectors of the matrix.


Diagonal test

In order to know if a real matrix is diagonal, one can use the method isDiagonal() : 

        double[][] diagonalMatrix = {{ 4.0, 0.0, 0.0, 0.0 },
                { 0.0,-1.0, 0.0, 0.0 },
                { 0.0, 0.0, 5.0, 0.0 },
                {0.0, 0.0, 0.0, 9.0 }};
        RealMatrix matrix = new Array2DRowRealMatrix(diagonalMatrix);
        matrix.isDiagonal(Precision.EPSILON);

Of course, because a matrix usually results from several operations which can introduce numerical errors, one has to give a threshold under which the non diagonal elements are considered to be zero ie the matrix is considered to be diagonal.


Invertible test

In order to know if a real matrix is invertible, one can use the method isInvertible(), this method checks if the n column vectors form a basis of Rn : 

        double[][] nonSingularMatrix = {{ 4.0, 2.0,-1.5, 2.0 },
                { 6.0, 8.0, 2.1, 2.5 },
                { 2.0, 1.0,-0.75, 1.0 },
                {-1.0, 0.0, 0.0, -0.5 }};
        RealMatrix matrix = new Array2DRowRealMatrix(nonSingularMatrix);
        matrix.isInvertible(Precision.EPSILON);

Of course, because a matrix usually results from several operations which can introduce numerical errors, one has to give a threshold under which the column vectors are considered linearly dependant.

UD decomposition

The UDDecompositionImpl class

The UDDecompositionImpl class is the one performing the UD-decomposition of a matrix.

If the RealMatrix A is not square, a NonSquareMatrixException is thrown. If the RealMatrix A is not symmetric, a NonSymmetricMatrixException is thrown. If the RealMatrix A is not positive definite, a NonPositiveDefiniteMatrixException is thrown.


Two constructors are available :

  • default constructor :

UDDecompositionImpl(matrix,relativeSymmetryThreshold,absolutePositivityThreshold)

with

  • matrix = matrix to factorize,
    • relativeSymmetryThreshold = threshold above which off-diagonal elements are considered too different and matrix not symmetric,
    • absolutePositivityThreshold = threshold below which diagonal elements are considered null and matrix not positive definite
  • basic constructor :

UDDecompositionImpl(matrix)

with

  • matrix = matrix to factorize with relativeSymmetryThreshold = DEFAULT_RELATIVE_SYMMETRY_THRESHOLD (1.0e-15) and absolutePositivityThreshold = DEFAULT_ABSOLUTE_POSITIVITY_THRESHOLD (0.0)

The following methods are available in it : 

final UDDecomposition udut = new UDDecompositionImpl(matrix);


  • get the U matrix
RealMatrix Umatrix = udut.getU();


  • get the D matrix
RealMatrix Dmatrix = udut.getD();


  • get the U^^t^^ matrix
RealMatrix UTmatrix = udut.getUT();


  • get the determinant
double d = udut.getDeterminant();


  • get the solver based on the UD decomposition
DecompositionSolver s = udut.getSolver();

Contents

Interfaces

The most relevant interfaces related to matrices are listed here :

Interface Summary Javadoc
Vector This interface represents a generic vector in a vectorial space or a point in an affine space. ...
RealMatrix Interface defining a real-valued matrix with basic algebraic operations. ...
SymmetricMatrix Interface for symmetric matrices. ...
Decomposition Interface for matrices decompositions. ...
DecompositionSolver Interface for matrices decompositions solvers. In particular thses solvers provides the inverse of a matrix. ...
UDDecomposition An interface to classes that implement an algorithm to calculate the UD-decomposition of a real matrix. ...

Classes

The most relevant classes related to matrices are listed here :

Class Summary Javadoc
Vector3D This class implements vectors in a three-dimensional space. ...
Matrix3D This is a real 3x3 matrix designed to be used in geometric calculations. It is compatible with the Vector3D type. ...
Array2DRowRealMatrix Implementation of RealMatrix using a double[][] array to store entries and LU decomposition to support linear system solution and inverse. ...
ArrayRowSymmetricMatrix Implementation of a symmetric matrix, implementing AbstractRealMatrix using a double[] array to store entries : storage convention is symmetric conventional full storage. ...
DiagonalMatrix Implementation of a diagonal matrix. ...
QRDecomposition Calculates the QR decomposition of a matrix. ...
LUDecomposition Calculates the LU decomposition of a matrix. ...
CholeskyDecomposition Calculates the Cholesky decomposition of a matrix. ...
SingularValueDecomposition Calculates the SVD decomposition of a matrix. ...
Récupérée de « http://patrius.cnes.fr/index.php?title=User_Manual_4.9_Matrices&oldid=3147 »