User Manual 4.16 Covariance
Introduction
Scope
Here are presented the covariance representation, how they can be associated to orbits and how they can be propagated.
Javadoc
These covariances representations are available in the package :
| Library | Javadoc |
|---|---|
| Patrius | Package fr.cnes.sirius.patrius.covariance |
Links
None as of now.
Useful Documents
None as of now.
Package Overview
None.
Features Description
Covariance
The Covariance class allows to create an instance of a covariance matrix (both for orbital and any other possible additional parameters). The covariance matrix is expressed as a SymmetricPositiveMatrix and a list of parameter descriptors List<ParameterDescriptor> that define the nature of each row/column of the input matrix.
If the list of parameter descriptors is provided as input when creating the Covariance object, the provided parameter descriptors are automatically associated with the rows/colums of the covariance matrix (in the order they are returned by the collection's iterator). The number of parameter descriptors must match the size the covariance matrix.
If the provided collection is null or empty, default parameter descriptors are used instead. These default descriptors are comprised of a single field descriptor for the PARAMETER_NAME, mapped to the string "p" + i, where i is the index of the corresponding row/column in the covariance matrix.
The following code shows an example on how to create a 6x6 covariance matrix, defining only orbital parameters.
// Covariance matrix
RealMatrix covMatrix =
new Array2DRowRealMatrix(new double[][] {
{ 4.0, 2.0, 2.0, 0.0, 0.0, 0.0 },
{ 2.0, 4.0, 2.0, 0.0, 0.0, 0.0 },
{ 0.0, 2.0, 4.0, 2.0, 0.0, 0.0 },
{ 0.0, 0.0, 2.0, 4.0, 2.0, 0.0 },
{ 0.0, 0.0, 0.0, 2.0, 4.0, 2.0 },
{ 0.0, 0.0, 0.0, 0.0, 2.0, 4.0 }});
final ArrayRowSymmetricPositiveMatrix mat = new ArrayRowSymmetricPositiveMatrix(SymmetryType.LOWER, covMatrix);
// Parameter descriptors one per row of the covariance matrix (orbital elements)
final List<ParameterDescriptor> paramDesc = new ArrayList<>();
final Map<FieldDescriptor<?>, Object> fieldDescriptorsMap = new LinkedHashMap<>();
// Orbital parameter descriptors
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.X);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "X");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
fieldDescriptorsMap.clear();
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.Y);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "Y");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
fieldDescriptorsMap.clear();
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.Z);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "Z");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
fieldDescriptorsMap.clear();
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.VX);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "VX");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
fieldDescriptorsMap.clear();
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.VY);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "VY");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
fieldDescriptorsMap.clear();
fieldDescriptorsMap.put(StandardFieldDescriptors.ORBITAL_COORDINATE, CartesianCoordinate.VZ);
fieldDescriptorsMap.put(StandardFieldDescriptors.PARAMETER_NAME, "VZ");
paramDesc.add(new ParameterDescriptor(fieldDescriptorsMap));
// Create Covariance object
Covariance cov = new Covariance(mat, paramDesc);
OrbitalCovariance
This class associates a Covariance instance with a given orbit, its date being the date of definition of the orbital covariance. The frame, orbit type (Cartesian, Keplerian, etc) and position angle type (mean, true, eccentric) in which it is expressed can also be specified at construction if they are not the frame, orbit type and position angle type of the associated orbit.
The covariance matrix must be at least six by six, where the first six rows/columns represent the uncertainty on the orbital parameters and the remaining ones represent the uncertainty on the additional parameters. The parameter descriptors of these first six rows/columns must be associated to an StandardFieldDescriptors#ORBITAL_COORDINATE orbital coordinate descriptor, and this descriptor must be mapped to a valid OrbitalCoordinate (one with the expected orbit type and state vector index).
The following code shows an example on how to create an OrbitalCovariance object.
// Create Covariance object (check how to create a Covariance in the specific page)
Covariance cov = new Covariance(mat, paramDesc);
// Define an orbit
// Default orbits
final Vector3D position = new Vector3D(1123783.5101019042, 5726033.748189187, 4006400.314678921);
final Vector3D velocity = new Vector3D(2084.2377426112616, 3863.6251103548725, -6087.970527060892);
final Vector3D acceleriation = new Vector3D(-1.820619869034308, -0.101556783658643, -4.503133105845696);
final PVCoordinates pv = new PVCoordinates(position, velocity, acceleriation);
final Orbit cartesianOrbit = new CartesianOrbit(pv, FramesFactory.getGCRF(), DATE, Constants.EGM96_EARTH_MU);
// Create an OrbitalCovariance. Since it is not specified at construction, the OrbitType, PositionAnge and Frame for the Covariance will be those of the input orbit.
OrbitalCovariance orbCov = new OrbitalCovariance(cov, cartesianOrbit);
The OrbitalCovariance object can be propagated and transformed into a different Frame, OrbitType and PositionAngle by using the available methods “shiftedBy” and “transformTo” respectively.
Note that the shift of the orbital covariance is based on a simple Keplerian model. It is not intended as a replacement for proper covariance propagation, but it should be sufficient for small time shifts or coarse accuracy.
It is also possible to transform the orbital covariance to a local orbital frame centered on a given orbit. The returned covariance is defined in cartesian coordinates, in the specified LOFType. Note that the local orbital frame uses the reference orbit as its PVCoordinatesProvider, which relies on a simple Keplerian model for the propagation. The LOF built is therefore only valid at the date of the reference orbit, unless it is frozen at this date (the LOF then becomes an inertial frame which can be used at other dates).
The behavior of this method is dependent on the selected PatriusConfiguration (see
) :
- If
PatriusConfigurationis MIXED_MODELS or OLD_MODELS, the pseudo-inertial frame is computed as the frame from the originalOrbitalCovariance(if pseudo-inertial), as the frame from the reference orbit (if pseudo-inertial) or as GCRF otherwise. - If
PatriusConfigurationis NEW_MODELS: the pseudo-inertial frame corresponds to the firstpseudoInertialFramefrom the reference orbit.
Then, for both cases, the LoF is created from this pseudo-inertial frame.
MultiOrbitalCovariance
The MultiOrbitalCovariance class corresponds to an OrbitalCovariance associated with multiple orbits.
This class associates a Covariance instance with multiple orbits, their common date being the date of definition of the orbital covariance. The frame, orbit type (Cartesian, Keplerian, etc) and position angle type (mean, true, eccentric) in which the covariance is expressed are specified at construction.
The covariance matrix must be at least N by N, where N is the number of orbits multiplied by the number of orbital parameters (ORBIT_DIMENSION).
Nevertheless, it can have a bigger size to take into account additional parameters. The latter can be of two different natures:
- Attached to a specific orbit (drag coefficient for example)
- Without associated orbit (environment parameter for example)
The parameters must be ordered according to the following manner: for each orbit, first the orbital parameters (ordered according to their index) then the additional parameters specific to the orbit. The additional parameters that are not attached to any orbit must be placed at the end.
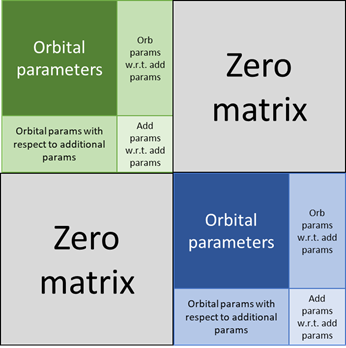
For the case of a MultiOrbitalCovariance for two satellites where both satellites are independent from each other and no additional parameters that are not attached to any orbit are configured, the resulting MultiOrbitalCovariance matrix would look like this (green is for the first satellite, blue is for the second).
The parameter descriptors of orbital parameters must be associated to an ORBITAL_COORDINATE descriptor, and these descriptors must be mapped to a valid OrbitalCoordinate (one with the expected orbit type and state vector index).
As for the case of the OrbitalCovariance, the MultiOrbitalCovariance object can be propagated and transformed into a different Frame, OrbitType and PositionAngle by using the available methods “shiftedBy” and “transformTo” respectively.
Note that the shift of the orbital covariance is based on a simple Keplerian model. It is not intended as a replacement for proper covariance propagation, but it should be sufficient for small time shifts or coarse accuracy.
It is also possible to transform the orbital covariance to a local orbital frame centered on a given orbit. The returned covariance is defined in cartesian coordinates, in the specified LOFType. Note that the local orbital frame uses the reference orbit as its PVCoordinatesProvider, which relies on a simple Keplerian model for the propagation. The LOF built is therefore only valid at the date of the reference orbit, unless it is frozen at this date (the LOF then becomes an inertial frame which can be used at other dates).
OrbitalCovarianceProvider
The OrbitalCovarianceProvider interface can be used by any class used for Orbital Covariance computation. It forces the user to implement the method getOrbitalCovariance(AbsoluteDate) which computes the OrbitalCovariance at the provided date. Moreover, it also allows the computation of the PVCoordinates of the reference orbit in the OrbitalCovariance object at the input date and in the selected frame.
A basic implementation of the OrbitalCovarianceProvider interface to allow for an easy covariance propagation can be found in the BasicOrbitalCovarianceProvider class.
BasicOrbitalCovarianceProvider
This class implements OrbitalCovarianceProvider by transforming an initial covariance with the partial derivatives of a spacecraft state provider.
To construct a BasicorbitalCovarianceProvider it is necessary to provide the initial covariance (Covariance), a SpacecraftStateProvider and a JacobiansMapper.
The initial covariance acts as the initial point from which to start the propagation. The spacecraft state provider used to propagate the initial covariance. The partial derivatives of the provider must be consistent with the initial covariance, i.e. must have the same date, frame, orbit type and position angle. Finally, the mapper is used to extract the partial derivatives from the spacecraft state.
To propagate the covariance, a state transition matrix is created from the jacobian matrix in the mapper, both for the orbital elements jacobian and the additional parameters jacobian. The state transition matrix values for the additional parameters with respect to themselves is one.
Finally, the propagated covariance is obtained as the quadratic multiplication of the initial covariance and the computed state transition matrix.
MultiOrbitalCovarianceProvider
Similar to the OrbitalCovarianceProvider, the MultiOrbitalCovarianceProvider interface can be used by any class used for multi orbital covariance computation. It forces the user to implement the method getMultiOrbitalCovariance(AbsoluteDate) which computes the MultiOrbitalCovariance at the provided date. Moreover, it also forces the implementation of a method that computes the orbital covariance provider extracting information from the original multi orbital covariance.
A basic implementation of the MultiOrbitalCovarianceProvider interface to allow for an easy covariance propagation can be found in the BasicMultiOrbitalCovarianceProvider class.
BasicMultiOrbitalCovarianceProvider
This class implements a MultiOrbitalCovarianceProvider by transforming an initial covariance with the partial derivatives of the corresponding spacecraft state providers.
To construct a BasicMultiOrbitalCovarianceProvider is necessary to provide the initial Covariance object and a Map where the different SpacecraftStateProviders as keys and the corresponding JacobiansMapper as values.
The spacecraft state providers are used to propagate the initial covariance. The mappers are used to extract partial derivatives from the spacecraft states.
The map must follow a set of conditions:
- Entries of this map must be ordered in the same order of the provided covariance.
- The partial derivatives of the providers must be consistent with the initial covariance, i.e. must have the same date, frame, orbit type and position angle.
If any of these conditions are not met, an error is raised.
The propagated MultiOrbitalCovariance is computed as an independent propagation of the different OrbitalCovariances represented in the matrix. So, even though initially the different covariance matrices expressed in the MultiOrbitalCovariance might share some correlation values, the propagation will not take into account these linkages.
First, a global state transition matrix is computed. This global state transition matrix is filled by concatenating diagonally the different individual state transition matrices obtained from each satellite. Each individual state transition matrix is computed as explained in the propagation of a BasicOrbitalCovarianceProvider.
Finally, the propagated MultiOritalCovariance is obtained as the quadratic multiplication of the initial MultiOrbitalCovariance and the computed global state transition matrix.
It is also possible to extract individual BasicOrbitalCovarianceProviders from the initial BasicMultiOrbitalCovarianceProvider object by using the getOrbitalCovarianeProvider method. To do so, the index of the spacecraft to be extracted from the global BasicMultiOrbitalCovarianceProvider is given as input. The initial object is truncated to select the information from the spacecraft corresponding to the input index.
Note that the BasicOrbitalCovarianceProvider is constructed taking as input covariance only the covariance of the orbital parameters and the additional parameters specific to the orbit. The additional parameters that are not attached to any orbit are not returned.
Content
Classes
| Class | Summary | Javadoc |
|---|---|---|
| Covariance | Class containing a covariance matrix and the list of parameter descriptors of every row in the covariance matrix | Covariance |
| AbstractOrbitalCovariance | An orbital covariance associates a Covariance instance with a given date and the frame, orbit type (Cartesian, Keplerian, etc) and position angle type (mean, true, eccentric) in which it is expressed. | [https://patrius.cnes.fr/images/upload/JavaDocs/V4.16/fr/cnes/sirius/patrius/covariance/AbstractOrbitalCovariance.html AbstractOrbitalCovariance] |
| OrbitalCovariance | Class containing a covariance matrix and its associated Orbit. | [https://patrius.cnes.fr/images/upload/JavaDocs/V4.16/fr/cnes/sirius/patrius/covariance/OrbitalCovariance.html OrbitalCovariance] |
| MultiOrbitalCovariance | Class containing a covariance matrix associated to multiple orbits | [https://patrius.cnes.fr/images/upload/JavaDocs/V4.16/fr/cnes/sirius/patrius/covariance/MultiOrbitalCovariance.html MultiOrbitalCovariance] |