User Manual 3.3 Dispersions

User Manual 3.3 Dispersions

Introduction

Scope

This section describes how dispersions are defined and used in the PATRIUS library. Dispersions are not to be mixed up with random generation (not detailed in this page). Dispersions always rely on a random generator.

Javadoc

The dispersions objects are available in the package org.apache.commons.math3.random in the Commons Math Library (and Commons Math add-ons). This package also handles random generation.

Library	Javadoc
Commons-Math	Package org.apache.commons.math3.random
Commons-Math addons	Package org.apache.commons.math3.random

Links

None as of now.

Useful Documents

None as of now.

Features Description

Random number generation

Distributed random number generation is based on using implementations of interface org.apache.commons.math3.random.NormalizedRandomGenerator. Each implementation of this interface provides a specific dispersion scheme. For instance, the following code will generate random numbers with Gaussian distribution of mean 0 and unit standard deviation:

final RandomGenerator g = new JDKRandomGenerator();
final NormalizedRandomGenerator generator = new GaussianRandomGenerator(g);
final double value = generator.nextNormalizedDouble();

As shown in the above example, building a dispersion object requires a random generator implementing org.apache.commons.math3.random.RandomGenerator interface.

Random vector generation

Correlated random vector generation is based on using implementations of interface org.apache.commons.math3.random.RandomVectorGenerator. Each implementation of this interface provides a specific dispersion scheme. For instance, the following code will generate uniformly correlated random vectors according to provided covariance matrix:

final RandomGenerator g = new JDKRandomGenerator();
final RandomVectorGenerator generator = new UniformlyCorrelatedRandomVectorGenerator(mean, covariance, 0, g);
final double[] value = generator.nextVector();

As shown in the above example, building a dispersion object requires a random generator implementing org.apache.commons.math3.random.RandomGenerator interface.

Contents

Interfaces

The library defines the following interfaces related to dispersions:

Interface	Summary	Javadoc
NormalizedRandomGenerator	Interface for normalized random generators	...
RandomVectorGenerator	Interface for random vector generators	...

Note: interface for random number generators is org.apache.commons.math3.random.RandomGenerator.

Classes

The library defines the following classes related to dispersions:

Class	Summary	Javadoc
GaussianRandomGenerator	Generator following Gaussian distribution	...
UniformRandomGenerator	Generator following uniform distribution	...
UncorrelatedRandomVectorGenerator	Generator for Gaussian uncorrelated vectors	...
CorrelatedRandomVectorGenerator	Generator for Gaussian correlated vectors	...
UniformlyCorrelatedRandomVectorGenerator	Generator for uniformly correlated vectors	...
UnitSphereRandomVectorGenerator	Generator for vectors isotropically located on a sphere	...

Correlated random vector generator

The user provides a covariance matrix and a random generator.
When using Gaussian correlated random vector generator:

• The covariance matrix root is extracted using a Cholesky decomposition. The number of columns of the root matrix corresponds to the rank of the provided covariance matrix.
• An uncorrelated vector of size the rank of the covariance matrix is generated using the provided random generator
• The final correlated vector is obtained by multiplying the covariance root matrix by this generated vector.

When using uniformly correlated random vector generator, the process is more complex:

• The covariance matrix is converted into a correlation matrix. Standard deviation vector is extracted from the process. Obtained correlation matrix must be positive semi-definite (all eigenvalues must be non negative).
• Spearman correction is applied to the correlation matrix. If corrected correlation matrix is not positive semi-definite, correction is not applied.

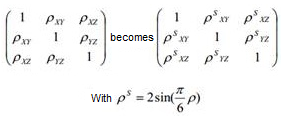
• The correlation matrix root is extracted using a Cholesky decomposition. The number of columns of the root matrix corresponds to the rank of the correlation matrix.
• A uncorrelated vector of size the rank of the covariance matrix is generated using the provided random generator
• The product of correlation matrix root L and uncorrelated vector T is then transformed to get a uniform law:

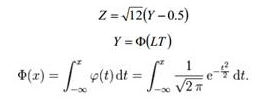
• The final correlated vector is obtained by linearly multiplying z by the standard deviation vector.

Tips & Tricks

None as of now.