User Manual 3.4.1 Spheroids

Definition

A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal equatorial radii. Assuming the XYZ coordinate system is such that the spheroid is centered and axis-aligned, the spheroids equation is given by:

[math]\displaystyle{ \mathcal{S} = \left\{ (x, y, z) \in \mathbb{R}^3 \middle/ {x^2 + y^2 \over a^2} + {z^2 \over b^2} = 1\right\} }[/math]

The equatorial radius is called the transverse radius whereas the polar radius [math]\displaystyle{ b }[/math] is the conjugate radius.

Implementation

The Spheroid object in the SIRIUS library implements the [MAT_GEO_EllipsoidInterface Ellipsoid interface]. Please refer to the Javadoc for a complete list of public methods.

Instantiation

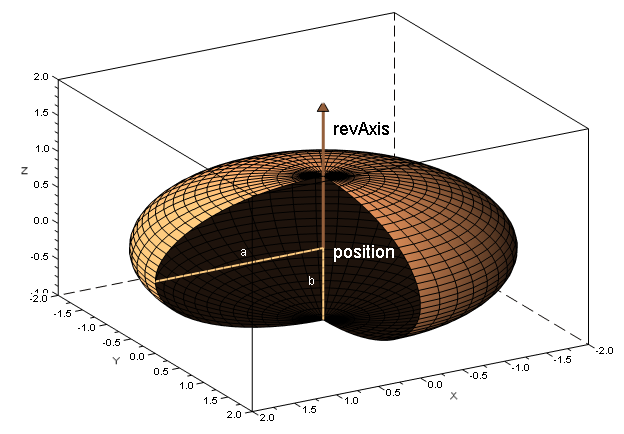
In order to instantiate a spheroid object, the user must specify the spheroids' center, it's axis of revolution and both semi-axis (the transverse radius [math]\displaystyle{ a }[/math] and the conjugate radius [math]\displaystyle{ b }[/math]). For example :

// Spheroid parameters
Vector3D position = new Vector3D(1, 2, 3);
Vector3D revAxis = new Vector3D(0, 1, 1);
double a = 2.0;
double b = 1.0;
// The spheroid itself
Spheroid mySpheroid = new Spheroid(position, revAxis, a, b);

Usage

Please refer to the [MAT_GEO_Home#HInteractions Interactions with other geometrical objects section] for methods inherited from the Shape interface.