User Manual 4.0 Guidance commands
Introduction
Scope
A guidance profile is an attitude law providing the computation of an instantaneous attitude without any reference to the satellite orbit, nor to its attitude laws sequence. The purpose of this section is to present the guidance profiles available through the Patrius library.
Javadoc
The guidance models and classes are available in the guidance package in the Patrius library.
| Library | Javadoc |
|---|---|
| Patrius | Package fr.cnes.sirius.patrius.guidance |
Links
None as of now.
Useful Documents
None as of now.
Package Overview
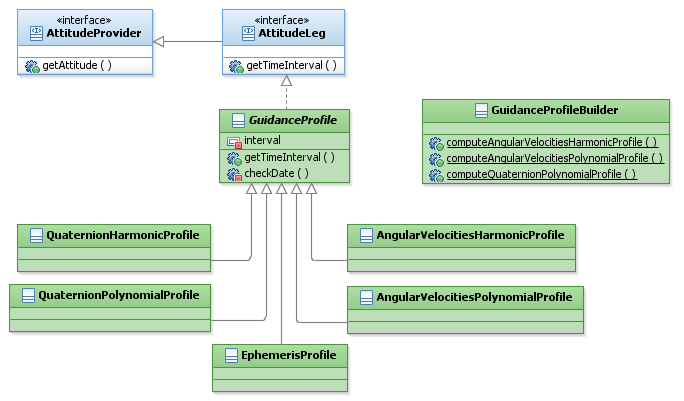
The following diagram shows the guidance package conception:
Features Description
Harmonic guidance profiles
The functions representing the angular velocity of the satellite and the quaternion (or the Euler angles) expressing its orientation can be represented by an harmonic profile. The harmonic profile is a [MAT_TPOL_Home#HFourierSeries Fourier decomposition] of a periodic function:
[math] S_n\left(f(x)\right) = a_0(f) + \sum_{k=1}^n\left(a_k(f)\cos\left(k x {2\pi\over T}\right) + b_k(f)\sin\left(k x {2\pi\over T}\right)\right) [/math]
The period T is generally computed knowing the nodes crossing periods.
The Fourier coefficients (n > 0) of [math]f[/math] (the angular velocity / quaternions / Euler angles function) are given by :
[math] a_0(f) = {1\over T}\int_{-T/2}^{T/2} \! f(t) \, \mathrm{d}t [/math]
[math] b_0(f) = 0 [/math]
[math] a_n(f) = {2\over T}\int_{-T/2}^{T/2} \! f(t) \cos\left(n t {2\pi\over T}\right) \, \mathrm{d}t [/math]
[math] b_n(f) = {2\over T}\int_{-T/2}^{T/2} \! f(t) \sin\left(n t {2\pi\over T}\right) \, \mathrm{d}t [/math]
Polynomial guidance profiles
A polynomial guidance profile is generally composed by several segments (a segment corresponds to a time interval). Each segment contains the coefficients for the computation of a polynomial law representing the quaternion (or the Euler angles), or the angular velocity of the satellite; this polynomial law is valid only inside the time interval associated to the segment.
For a quaternion, the polynomials are defined as :
[math]Qc_k(t) = \begin{pmatrix} \displaystyle\sum_{i=0}^n {a_0}_k^i \left( t-t_k \over {\Delta t} \right) \\ \displaystyle\sum_{i=0}^n {a_1}_k^i \left( t-t_k \over {\Delta t} \right) \\ \displaystyle\sum_{i=0}^n {a_2}_k^i \left( t-t_k \over {\Delta t} \right) \\ \displaystyle\sum_{i=0}^n {a_3}_k^i \left( t-t_k \over {\Delta t} \right) \end{pmatrix}[/math]
And for the angular velocity :
[math]\Omega c_k(t) = \begin{pmatrix} \displaystyle\sum_{i=0}^n {a_x}_k^i \left( \frac{t-t_k}{\Delta t} \right) \\ \displaystyle\sum_{i=0}^n {a_y}_k^i \left( \frac{t-t_k}{\Delta t} \right) \\ \displaystyle\sum_{i=0}^n {a_z}_k^i \left( \frac{t-t_k}{\Delta t} \right) \end{pmatrix}[/math]
Getting Started
Build an harmonic guidance profile from an attitude law
Given :
- an AttitudeLawLeg,
- a PVCoordinatesProvider,
- a Frame,
- a reference date
tref, - a spin function period,
- a spin decomposition order,
- an integration type,
- an integration step,
one can build an angular velocities guidance profile using the code snippet below :
profile = GuidanceProfileBuilder.computeAngularVelocitiesHarmonicProfile(attitude, prop, gcrf, tref, period, order, IntegrationType.WILCOX_4, KinematicsToolkit.DEFAULT_8HZ);
Contents
Interfaces
None.
Classes
| Class | Summary | Javadoc |
|---|---|---|
| KinematicsToolkit | This class contains static methods performing kinematics operations. | ... |
| GuidanceProfile | Abstract class representing a guidance profile. | ... |
| GuidanceProfileBuilder | This class creates guidance profiles from an attitude law. | ... |
| QuaternionHarmonicProfile | Object representing a quaternion guidance profile, calculated with Fourier series. | ... |
| QuaternionPolynomialProfile | Object representing a quaternion guidance profile, calculated with polynomials. | ... |
| QuaternionPolynomialSegment | Object representing a quaternion polynomial guidance profile on a segment. | ... |
| AngularVelocitiesHarmonicProfile | Represents an angular velocities guidance profile, calculated with Fourier series. | ... |
| AngularVelocitiesPolynomialProfile | Represents an angular velocities guidance profile, calculated with polynomial functions. | ... |
| AngularVelocitiesPolynomialSegment | Object representing an angular velocity polynomial guidance profile on a segment. | ... |
