User Manual 4.6 Numerical propagation

Introduction

Scope

This section describes the numerical propagator provided by the Patrius Library: basic orbit propagation, mass, partial derivatives and additional equations. Generic features about propagators as well as other types of propagators are detailed [ORB_PGEN_Home here].

Javadoc

Some of the numerical propagation packages available are listed here :

Library	Javadoc
Orekit	Package fr.cnes.sirius.patrius.propagation.numerical

Links

You can find more general information on propagation on the [ORB_PGEN_Home Propagation page ].

Useful Documents

None as of now.

Package Overview

Partial Derivatives

The PATRIUS library offers a comprehensive API that allows computing derivatives using Finite Differences, but also retreiving analytically computed partial derivatives where applicable. The supportParameters() and supportJacobiansParameters() methods from the interfaces given hereunder indicate the user if finite differences and jacobians can be computed.

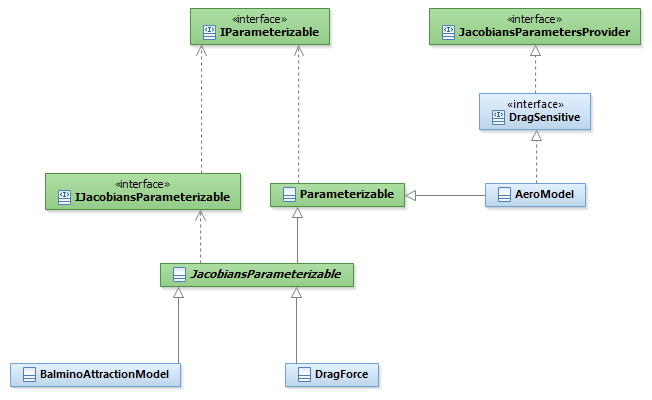
Features description

Propagation

See : [FDY_SST_Home SpacecraftState description]

Numerical propagation can be executed in cartesian, equinoctial, keplerian and circular parameters. By default, equinoctial parameters are used.

A loss of accuracy occurs when a numerical propagator using a fixed step RK4 integrator propagates a bulletin using cartesian parameters.

Dormand-Prince integrators

Adaptive stepsize Dormand-Prince integrators are commonly use in space mechanics. A 5th order and a 8th order Dormand-Prince integrator is available.
They have the particularity to have an adaptive step size: during the integration, the integrator tries to keep the integration step as large as possible to save some computation time. The integrator computes the integration step to use by estimating the error made compared to a threshold. The smaller the stepsize, the higher the dynamics of the system.
As a result, the user is required to provide the following information:

The minimum and maximum allowed step size. The minimum step size should be small enough to handle any integration of the user dynamics. The maximum step size should be high enough to reduce computation times when the dynamics is slow.
The absolute and relative tolérances. These tolerances are used to estimate the current integration step: the integrator reduces the step size until estimated error is below these tolerances. Warning: it does not mean the accuracy of your integration will be below these tolerances! But only that over one integration step, the use of this integrator should not degrade the accuracy of the result more than the fixed tolerance.

As a rule of thumb, the following instantiation is good for orbit dynamics (stepsize in [0.01s, 500s], absolute tolerance being { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8} and relative tolerance being 1e-10:

final double[] vecAbsoluteTolerance = { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8};
final double[] vecRelativeTolerance = { 1e-10, 1e-10, 1e-10, 1e-10, 1e-10, 1e-10};
final FirstOrderIntegrator integrator = new DormandPrince853Integrator(0.01, 500., vecAbsoluteTolerance, vecRelativeTolerance);

When dealing with another dynamics (semi-analytical propagation, etc.), other parameterization may be more suitable. Alike the code example above, one has to specify in which parameters type the propagation has to be performed, calling setOrbitType(OrbitType) on the propagator (Orbitype.CARTESIAN for cartesian parameters for example).

Important notice

Dormand-Prince integrators (as well as Higham-hall integrator) uses only states whose tolerance has been defined to estimate error and deduce integration step.
Tolerance is defined if not set to [absolute tolerance = +inf, relative tolerance = 0].
By default, tolerances are not set for partial derivatives. As a result, propagation with or without partial dérivatives will return the exact same PV coordinates.

Note that if provided tolerance requires a time step lower than provided minimum stepsize then an exception will be thrown by default. Every adaptive stepsize integrator provides constructors to circumvent this behavior: in that case, if a lower time step than minimum stepsize is required then minimum stepsize is used (hence tolerance is not respected for this step). This is particularly useful for some particular dynamics such as reentry.

Cowell integrator

CowellIntegrator

is a very efficient second order variable-step integrator which uses a predictor-corrector scheme. This integrator is a second order, which means it directly integrate an equation y" = f(y, y', t).

Two parameters are to be provided to the integrator:

Integrator order up to order 20
Integrator absolute and relative tolerances

Best results are obtained with following parameters:

Integrator order: 9
Tolerances: between 1E-10 and 1E-12

With these parameters, accuracy is between 0.1mm an 10mm for a one-day propagation, independently of force models.

Getting Started

Propagation

Basic propagation

Here is presented a basic instanciation of the numerical propagator with an input state built from an orbit and a mass provider.

See : [SPC_VBU_Home Building assembly]

// Initial orbit
final AbsoluteDate date = new AbsoluteDate(2000, 3, 1, TimeScalesFactory.getTT());
final double mu = Constants.EGM96_EARTH_MU;
final Frame referenceFrame = FramesFactory.getGCRF();
final Orbit orbit = new KeplerianOrbit(7500000, 0.001, 0.40, 0, 0, 0,PositionAngle.MEAN, referenceFrame, date, mu);
 
// Initial mass provider
final MassProvider massModel = new MassModel(assembly);
 
// Initial SpacecraftState 
final SpacecraftState initialState = new SpacecraftState(orbit, massModel);
 
// integrator tolerances for the orbital parameters
final double[] vecAbsoluteTolerance = { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8};
final double[] vecRelativeTolerance = { 1e-10, 1e-10, 1e-10, 1e-10, 1e-10, 1e-10};
// integrator and propagator
final FirstOrderIntegrator integrator = new DormandPrince853Integrator(0.01, 500., vecAbsoluteTolerance, vecRelativeTolerance);
final NumericalPropagator p = new NumericalPropagator(integrator);
 
// Propagate in cartesian parameters
p.setOrbitType(OrbitType.CARTESIAN);
 
// Initialize state
p.setInitialState(initialState);
 
// add equations associated with mass model : compulsory if maneuvers are present !!! Mass provider must be mass provider used in force models.
p.setMassProviderEquation(massModel);
 
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));

In order to add force models to your propagator use the method NumericalPropagator.addForceModel(). Advice: in order to minimize absorption effects leading to reduced accuracy, add force models from least perturbing force to highest perturbing force.
Example: for LEO orbits, drag should be added in last.

Adding mass to state vector

Mass is a particular additional state, since it is common state in orbital propagation. Propagation with other additional states is detailed in next section.

Including mass states in propagation requires two step:

Add mass initial states to state vector:

This is performed by providing a MassProvider to the initial SpacecraftState. Mass information is automaticaly stored as additional states of the SpacecraftState.

Add mass equations to propagator:

For each mass additional state associated with the SpacecraftState, the corresponding additional equation are added to the numerical propagator using setMassProviderEquation(MassProvider). Important notice: this method should be called only once and provided mass provider must be mass provider used in force models for global propagation consistency.

An example using mass propagation is detailed in next section.

Propagation with additional states

It is possible to propagate the complete SpacecraftState including additional states. It could be particularly interesting to propagate additional states if, for example, some other variables need the dynamical spacecraft state to be computed. These additional states are related to differential equations that have to be given to the numerical propagator. They will be integrated with the same integrator scheme as the motion equations and at the same time. It is also possible to define variation tolerance values specifically for each additional state, so that a variable step integrator can take these into account and reduce its step to compute additional states accurately.

In practical terms, the user has to build the additional equation by implementing the interface "AdditionalEquation".

These additional equations are given to the propagator thanks to the following methods :

addAdditionalEquation(AdditionalEquation)
addAttitudeEquation(AttitudeEquation) (see next part)
setMassProviderEquation(MassProvider) (This method should be called only once, see above section)

The initial value of the additional states are stored in the initial SpacecraftState given to the propagator. The method "setAdditionalStateTolerance(String, double[], double[])" may be used to add variation tolerance values (absolute and relative) for the state. An additional equation should be identified by the user in an unequivocal way by a name (String) which is a mandatory attribute. The link between the additional state and the additional equation is done at the beginning of the propagation. At the beginning of the propagation, it is also checked that the additional states size correspond with the additional tolerances fixed in the propagator.
The following example shows how to propagate a SpacecraftState with a mass and one additional state.

// Initial SpacecraftState 
SpacecraftState initialState = new SpacecraftState(orbit, massModel);
 
// add additional state (of size 3) to the SpacecraftState
final String stateName = "state1";
initialState = initialState.addAdditionalState(stateName, new double[]{1., 2., 3.});
 
// Initialize state
p.setInitialState(initialState);
 
// add equations associated with mass model (Mass provider must be mass provider used in force models)
p.setMassProviderEquation(massModel);
 
// add additional equation associated with the additional state
p.addAdditionalEquations(additionalEquation);
 
// tolerances (of size 3) for the additional state :
final double[] absoluteTol = { 1e-5, 1e-5, 1e-5 };
final double[] relativeTol = { 1e-10, 1e-10, 1e-10 };
p.setAdditionalStateTolerance(stateName, absoluteTol, relativeTol);
 
// Propagate in cartesian parameters
p.setOrbitType(OrbitType.CARTESIAN);
 
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));

It is possible to get a feedback of the additional states evolution throughout the propagation. To that purpose, the user should create a step handler which implements the interface "PatriusStepHandler" and set the propagator to "master mode". The main method of the step handler is the method "handleStep(PatriusStepInterpolator, boolean) " which has to be designed by the user according to what he wants to do at the end of each integration step. For example, in order to get a feedback of the additional states once the propagation is performed, the user could design this method in the following manner :

        @Override
        public void handleStep(final PatriusStepInterpolator interpolator, final boolean isLast)
                throws PropagationException {
 
            SpacecraftState currentState;
            Map<String, double[]> addStates;
            try {
 
                currentState = interpolator.getInterpolatedState();
                addStates = currentState.getAdditionalStates();
 
                datesList.add(currentState .getDate());
                pv.add(currentState.getPVCoordinates());
                addStatesMap.add(currentState.getAdditionalStates());
 
            } catch (PatriusException e) {
                e.printStackTrace();
            }
        }

If you want to keep the provided interpolator for later use, add in handleStep method:

((AdaptedStepHandler) interpolator).copy();

To continue the previous example :

// propagation
final StateObserver stepHandler = new StateObserver();
 
p.setMasterMode(stepHandler);
 
p.resetInitialState(new SpacecraftState(orbit));
 
p.propagate(date.shiftedBy(propagationDuration));
 
final List<AbsoluteDate> dates = stepHandler.getDatesList();
final List<Double> mass = stepHandler.getAddStateList();
final List<PVCoordinates> pv = stepHandler.getDatesList();

Warning : when using a fixed step Handler (PatriusFixedStepHandler), users must access to the additional states (such as the thruster' s mass during a maneuver) by the spacecraft AND NOT using the Assembly since the Assembly is synchronized only once per integration step. In any other case (using an PatriusStepHandler for instance), both assembly and spacecraft can be used to retrieve additional states.

Propagation of the attitudes : two possible treatments

To propagate the Attitude, two treatments could be applied :

compute the attitude with an AttitudeProvider :setAttitudeProvider(AttitudeProvider).
It is possible to deals with :
- a single attitude by calling setAttitudeProvider(AttitudeProvider)
- two attitudes by calling setAttitudeProviderForces(AttitudeProvider) or setAttitudeProviderEvents(AttitudeProvider). It is not possible to call setAttitudeProvider(AttitudeProvider) and setAttitudeProviderForces(AttitudeProvider) (or setAttitudeProviderEvents(AttitudeProvider))
propagate the attitude as a 7-dimension additional state :addAttitudeEquation(AttitudeEquation).
In practical terms, the user has to build the additional equation by extending the abstract class AttitudeEquation, call addAttitudeEquation(AttitudeEquation). The additional state corresponding with the attitude is automatically add to the additional states map of the initial SpacecraftState. An AttitudeEquation is associated with an AttitudeType :
- ATTITUDE : if a single attitude treatment is done. If the user wants to propagate only one attitude.
- ATTITUDE_FORCES and ATTITUDE_EVENTS : if a double attitude treatment is done. If the user wants to propagate the attitude for forces computation and the attitude for events computation. See : [FDY_SST_Home SpacecraftState description]
  It is not possible to add an attitude equation in type ATTITUDE and one in type ATTITUDE_FORCES or ATTITUDE_EVENTS.

The following example shows how to propagate a SpacecraftState with an attitude added to the additional states map.

// Initial SpacecraftState
SpacecraftState initialState = new SpacecraftState(orbit, attitude);
// Initialize state
p.setInitialState(initialState);
// add equation associated with the attitude
p.addAttitudeEquation(new AttitudeEquation(AttitudeType.ATTITUDE) {
   public void computeDerivatives(SpacecraftState s, TimeDerivativesEquations adder) throws PatriusException {...}
});
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));

The following example shows how to propagate a SpacecraftState with two attitude (one added to the additional states map, the other computed with the AttitudeProvider).

// Initial SpacecraftState
SpacecraftState initialState = new SpacecraftState(orbit, attitudeForces, attitudeEvents);
// Initialize state
p.setInitialState(initialState);
 
// add equations associated with attitude for forces computation
p.addAttitudeEquation(new AttitudeEquation(AttitudeType.ATTITUDE_FORCES) {
    public void computeDerivatives(SpacecraftState s, TimeDerivativesEquations adder) throws PatriusException {...}
});
 
// add attitude provider for events computation : attitude law aligned with EME2000
final AttitudeProvider attProv = new ConstantAttitudeLaw(FramesFactory.getEME2000(), Rotation.IDENTITY);
p.setAttitudeProviderEvents(attProv);
 
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));

Partial derivatives equations

PATRIUS provides an implementation of the interface "AdditionalEquation". This set of additional equations computes the partial derivatives of the state (orbit) with respect to initial state and force models parameters.

This set of equations is automatically added to a numerical propagator in order to compute partial derivatives of the orbit during a propagation. This is useful in orbit determination applications. The force models implement analytical methods to compute partial derivatives with respect to state or force models parameters. If not, the finite difference method is applied.

Partial derivatives with respect to state (position or velocity) can be tuned or disabled:

They can be disabled for every force inheriting GradientModel using the provided constructors.
For potential models (excluding Droziner model), order and degree can be tuned differently for acceleration computation and partial dérivatives computation.

The general principles are described in the above section Additional state. An example is given here to see how to propagate jacobians throughout an orbit. We call dYdY0 the partial derivatives of the state with respect to initial state and dYdP the partial derivatives of the state with respect to force models parameters.

First, the user has to add the partial derivatives equations of the state. Upon construction, this set of equations is automatically added to the propagator by calling its "NumericalPropagator.addAdditionalEquations(AdditionalEquations)" method. So there is no need to call this method explicitly for these equations.

After that, the user has to set the initial value of the jacobians with respect to state and parameters, using the "PartialDerivativesEquations.setInitialJacobians(SpacecraftState, int)" method (or "setInitialJacobians(SpacecraftState, double[][])"). This method is equivalent to call "setInitialJacobians(SpacecraftState, double[][], double[][])" with dYdY0 set to the identity matrix and dYdP set to a zero matrix. Other similar methods are provided if the user wants to specifically set initial Jacobians with respect to state or to one particular parameter ("setInitialJacobians(SpacecraftState, Parameter, double[])".

A set to a zero matrix. Other similar methods are provided if the user wants to specifically set initial Jacobians with respect to state or to one particular parameter ("setInitialJacobians(SpacecraftState, Parameter, double[])".

To use the jacobians, it is necessary to define a mapper between one-dimensional additional state and two-dimensional jacobians.

// we assume that a propagator "propagator" has been built with its initial state "initialState"
 
// add the partial derivatives of the state with respect to initial state,
// with a name to identify it     
final PartialDerivativesEquations partials = new PartialDerivativesEquations("PDE", propagator);
 
// set the initial value of the jacobians
// here state dimension = 6 and parameter dimension = 0
partials.setInitialJacobians(initialState, 0);
// get a mapper between two-dimensional jacobians and one-dimensional additional state
// with the same name as the instance
final JacobiansMapper mapper = partials.getMapper();
[...]

In order to get the jacobians throughout the propagation, the user can create a step handler which implements the interface "PatriusStepHandler" and set the propagator to "master mode". The example shows how to get jacobians during the propagation. The following class "JacobiansHandler" implements "PatriusStepHandler" (the main methods are given hereafter).

        // step handler constructor
        public JacobiansHandler(final JacobiansMapper inMapper, final AbsoluteDate inDate) {
            this.mapper = inMapper;
            this.date = inDate;
            dYdY0 = new double[mapper.getStateDimension()][mapper.getStateDimension()];
            dYdP = new double[mapper.getStateDimension()][mapper.getParameters()];
        }
 
 
        @Override
        public void handleStep(final PatriusStepInterpolator interpolator, final boolean isLast)
                throws PropagationException {
            try {
                if (date == null) {
                    // we want to pick up the Jacobians at the end of last step
                    if (isLast) {
                        // set the interpolated date which is the current grid date (the last step)
                        interpolator.setInterpolatedDate(interpolator.getCurrentDate());
                    }
                } else {
                    // we want to pick up some intermediate Jacobians
                    final double dt0 = date.durationFrom(interpolator.getPreviousDate());
                    final double dt1 = date.durationFrom(interpolator.getCurrentDate());
                    if (dt0* dt1 > 0) {
                        // the current step does not cover the pickup date
                        return;
                    } else {
                        // set the interpolated date
                        interpolator.setInterpolatedDate(date);
                    }
                }
                // get the interpolated state at the current interpolated date
                final SpacecraftState state = interpolator.getInterpolatedState();
                // get the Jacobian with respect to state-> dYdY0 array
                dYdY0 = mapper.getStateJacobian(state);
                // get the Jacobian with respect to parameters-> dYdP array
                dYdP = mapper.getParametersJacobian(state);
                // get the Jacobian with respect to parameter 1-> dYdP1 array
                dYdP1 = mapper.getParametersJacobian(parameter1, state);
            } catch (PropagationException pe) {
                throw pe;
            } catch (PatriusException oe) {
                throw new PropagationException(oe);
            }
 
        } 
 
        // Method to get the jacobian with respect to initial state
        public double[][] getdYdY0() {
            return dYdY0;
        }

To continue with the main program, a way to get the jacobians and to use it could be the following:

[...]
        // add a step handler to get the jacobian matrix corresponding to the last date
        // can be used to get the jacobians corresponding to a given date
        final JacobiansHandler jacobiHandler = new JacobiansHandler(mapper, initialDate.shiftedBy(dt));
        propagator.setMasterMode(jacobiHandler);
 
        // propagate the orbit until initialDate+dt
        final SpacecraftState finalState = propagator.propagate(initialDate.shiftedBy(dt));
 
        // get the jacobian matrix with respect to initial state at the final date
        final double[][] dYdY0 = jacobiHandler.getdYdY0();
 
        // examples using jacobians...
 
        // convert dYdY0 into a RealMatrix
        final RealMatrix mat = new Array2DRowRealMatrix(dYdY0);
 
        // invert mat, using LU decomposition
        final RealMatrix matInverse = new LUDecomposition(mat).getSolver().getInverse();
[...]

Note : the dYdY0 terms are given according to the orbit type known to the propagator. If one wants to compute the partial derivatives with equinoctial parameters, then one should specify it to the propagator first, using the method NumericalPropagator.setOrbitType(OrbitType). Additionally, it is also important to specify the correct orbit position angle type (true, mean or eccentric- if the orbit requires it), using the methods NumericalPropagator.setPositionAngleType(PositionAngle).

Interface	Summary	Javadoc
AdditionalStateProvider	This interface represents providers for additional state data beyond SpacecraftState.	...
AdditionalEquations	This interface allows users to add their own differential equations to a numerical propagator.	...
ModeHandler	Common interface for all propagator mode handlers initialization.	...
TimeDerivativesEquations	Interface summing up the contribution of several forces into orbit and mass derivatives.	...

Classes

Class	Summary	Javadoc
NumericalPropagator	This class propagates SpacecraftState using numerical integration.	...
AttitudeEquation	This class represents attitude differential equations.	...
IntegratedEphemeris	This class stores sequentially generated orbital parameters for later retrieval.	...
SimpleAdditionalStateProvider	This class implements AdditionalStateProvider interface. It simply handles a list of dates associated to additional state vectors. For a given date it returns the associated additional state vector or a propagation exception if this date is not found. This class will be basically used with a PVCoordinatePropagator.	...

User Manual 4.6 Numerical propagation

Sommaire

Introduction

Scope

Javadoc

Links

Useful Documents

Package Overview

Partial Derivatives

Features description

Propagation

Dormand-Prince integrators

Cowell integrator

Getting Started

Propagation

Basic propagation

Adding mass to state vector

Propagation with additional states

Propagation of the attitudes : two possible treatments

Partial derivatives equations

Contents

Interfaces

Classes

Menu de navigation

Outils personnels

Espaces de noms

Variantes

Affichages

Plus

Rechercher

PATRIUS

Evolutions

User Manual

Tutorials

Links

Navigation

Outils

Imprimer / exporter