User Manual 3.3 Force models : Différence entre versions
(→Solar radiation pressure) |
(→Solar radiation pressure with ellipsoid occulting body) |
||
| Ligne 376 : | Ligne 376 : | ||
===== Solar radiation pressure with ellipsoid occulting body ===== | ===== Solar radiation pressure with ellipsoid occulting body ===== | ||
| − | Before implementing the solar radiation pressure (that takes into account Earth flattening), one has to define a vehicle with radiative properties. To do so, it is advised to consult the page which describes how to build and use [[User Manual 3.3 Assemblies in PATRIUS: Presentation|the Assembly]] ([User Manual 3.3 Assemblies in PATRIUS: Building and using an assembly|see also...]). | + | Before implementing the solar radiation pressure (that takes into account Earth flattening), one has to define a vehicle with radiative properties. To do so, it is advised to consult the page which describes how to build and use [[User Manual 3.3 Assemblies in PATRIUS: Presentation|the Assembly]] ([[User Manual 3.3 Assemblies in PATRIUS: Building and using an assembly|see also...]]). |
The following code snippet allows the user to create an instance of the ForceModel class that can be passed to the NumericalPropagator. This instance will calculate the SRP by computing penumbra and umbra events for a flattened Earth. | The following code snippet allows the user to create an instance of the ForceModel class that can be passed to the NumericalPropagator. This instance will calculate the SRP by computing penumbra and umbra events for a flattened Earth. | ||
Version du 1 mars 2018 à 13:46
Introduction
Scope
The scope of this section is to present the force models available in PATRIUS. Forces models can be added to Patrius Numerical propagator.
Javadoc
| Library | Javadoc |
|---|---|
| Orekit | NOTFOUND |
| Orekit | Package fr.cnes.sirius.patrius.forces.drag |
| Orekit | Package fr.cnes.sirius.patrius.forces.gravity |
| Orekit | Package fr.cnes.sirius.patrius.forces.gravity.potential |
| Orekit addons | Package fr.cnes.sirius.patrius.forces.gravity.variations |
| Orekit addons | Package fr.cnes.sirius.patrius.forces.gravity.variations.coefficients |
| Orekit addons | Package fr.cnes.sirius.patrius.forces.gravity.tides |
| Orekit | Package fr.cnes.sirius.patrius.forces.radiation |
| Orekit addons | Package org.orekit.forces.radiation |
| pbase | Package fr.cnes.sirius.patrius.forces |
Links
Algorithms used
The algorithms used for the tides (earth and ocean) are taken from the FORTRAN code in ZOOM- see Manuel algorithmique OBELIX below. The routines used as references are given hereunder :
- f_maroce.f90
- fmf_ccadmt.f90
- obelixutil.f90
- mc_argfond.f90
The algorithms used for the rediffused radiation pressure are taken from OBELIX library. The routines used as references are given hereunder :
- fpr_elements
- fai_daccdd
The method used to compute the resulting acceleration is the same as that used in the Cunnigham attraction model.
Other Documents
- Manuel algorithmique OBELIX (Obelix-NT-12-1, version 4 révision 0 du 30/03/2012)
Useful Documents
- Cunningham; Leland E., On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite (Celestial Mechanics 2), Lockheed Missiles and Space Company, Sunnyvale and Astronomy Department University of California, Berkeley), 1970. Available here.
- Drozyner; A., Recurrent calculation of gravitational acceleration of a satellite, Acta Astronomica, vol. 27, no. 1, 1977, p. 15-22. Available here.
Package Overview
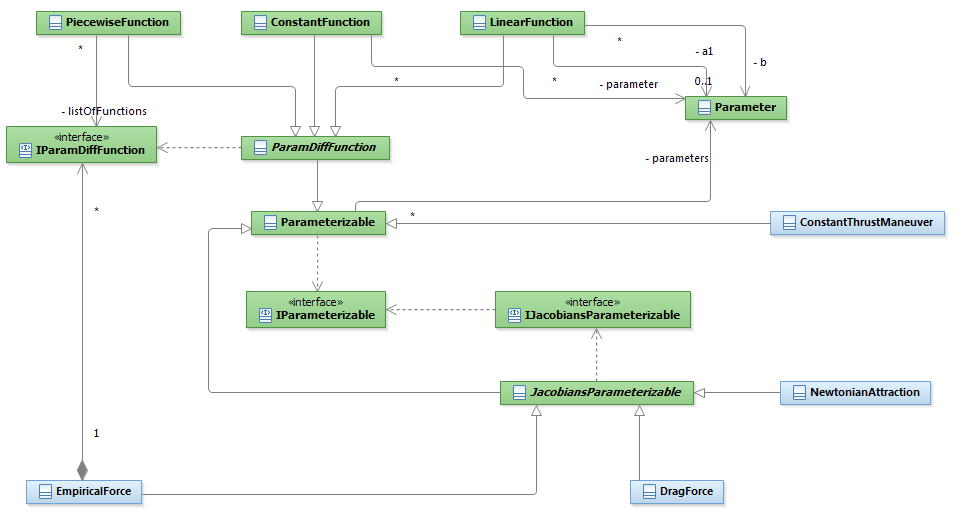
Parameterizable models
Parameterizable models are supported.
A parameter of a model can be define as Paramater (given its name and value), a constant function, a linear function or a piecewise function.
All parameters are handled in a the Parameterizable class.
In case of a using a function for a model's paramater (Fx), the Parameter defined are automatically stored in the super class Parameterizable.
Note that in this case, it is not Fx that is stored but ax and bx (with Fx = ax*t + bx).
Tides
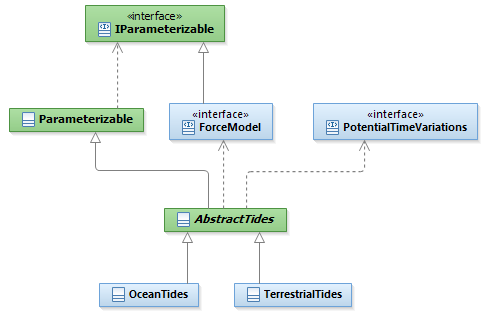
The architecture of the org.orekit.forces.gravity.tides package is given hereunder. The classes OceanTides and TerrestrialTides extend AbstractTides.
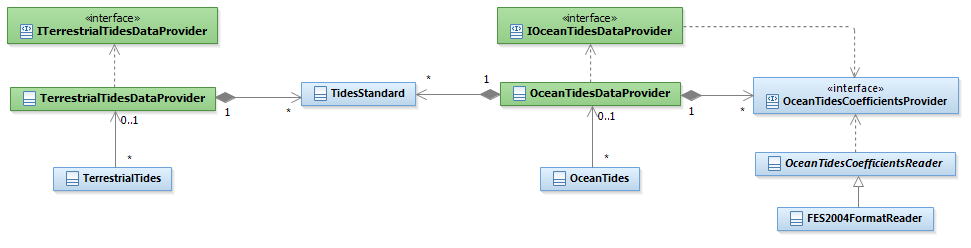
The architecture of the org.orekit.forces.gravity.tides.coefficients package is given hereunder. The user must use the OceanTidesCoefficientsFactory class to get an instance of the OceanTidesCoefficientsProvider interface, and pass it as an argument to the constructor of the OceanTidesDataProvider class.
Features Description
Available force models
The force models implemented are :
- Central gravity force :
- Normalized attraction model : Balmino
- Unnormalized attraction models : Cunningham and Droziner
- Third body gravity force
- Atmospheric drag
- Based on DTM2000, JB2006, US76 and MSIS2000 atmosphere models and solar activity data
- Solar radiation pressure force
- Terrestrial tides: the earth tide is the deformation of the solid earth caused by the gravitational attraction of the Sun and moon. The standard used for constants and Love numbers is IERS 2003. The potential of the earth deformation is composed of 3 terms:
- the potential of earth tide: the potential is computed for degree 2 and takes into account complex Love numbers for long period (k20), diurnal (k21) and semi-diurnal (k22) terms. The potential for degree 3 is optional.
- the frequency correction of the Love numbers is also optional. It is applied on diurnal Love number (k21) [see Wahr and Zhu theory].
- the ellipticity correction is also optional. The ellipticity effect involves corrections on terms of degree 4 [see Wahr theory, 1981]
- Ocean Tides
- Solar pressure rediffused by the earth (albedo pressure and infrared emissivity pressure)
- Empirical forces
- Relativistic effects :
- Schwarzschild effect : the most important effect
- Coriolis effect (or geodetic precession)
- Lense-Thirring effect : due to the rotation of central body
The acceleration derivatives implemented are :
|=(% colspan="6" %)Force model|=(% colspan="6" %)wrt Position|=(% colspan="3" %)wrt Velocity|=(% colspan="9" %)wrt additional parameters |=(% colspan="15" %)|=(% colspan="3" %)Parameter|=(% colspan="3" %)ParamDiffFunction|=(% colspan="3" %)Parameter or ParamDiffFunction from a model |(% colspan="6" %)Cunningham attraction|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Balmino attraction|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Droziner attraction|(% colspan="6" %)no|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Newtonian attraction|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)MU|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Variable potential model|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Third body attraction|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Drag force|(% colspan="6" %)yes|(% colspan="3" %)yes|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)DragSensitive(AeroModel: Cx, Cn, Ct) |(% colspan="6" %)Direct solar radiation|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)Reference flux|(% colspan="3" %)no|(% colspan="3" %)RadiationSensitive(DirectRadiativeModel : k0, ka, ks, kd) |(% colspan="6" %)Rediffused solar radiation|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)RediffusedRadiationSensitive(RediffusedRadiativeModel : k0Ir, k0Al, ka, ks, kd) |(% colspan="6" %)Empirical force|(% colspan="6" %)NA(null derivatives)|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)AX_COEFFICIENT, AY_COEFFICIENT, AZ_COEFFICIENT, BX_COEFFICIENT, BY_COEFFICIENT, BZ_COEFFICIENT, CX_COEFFICIENT, CY_COEFFICIENT, CZ_COEFFICIENT|(% colspan="3" %)no |(% colspan="6" %)Ocean tides|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Terrestrial tides|(% colspan="6" %)yes|(% colspan="3" %)NA(null derivatives)|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Schwarzschild|(% colspan="6" %)yes|(% colspan="3" %)yes|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Coriolis|(% colspan="6" %)NA(null derivatives)|(% colspan="3" %)yes|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no |(% colspan="6" %)Lense-Thirring|(% colspan="6" %)yes|(% colspan="3" %)yes|(% colspan="3" %)no|(% colspan="3" %)no|(% colspan="3" %)no
Note : The partial derivatives of the Balmino acceleration model are that of the Cunningham attraction model. They are thus limited in degree and order (sum should be lower or equal than approx. 160).
Gravity potential
Modèle:SpecialInclusion prefix=$theme sub section="Gravity potential"/
Tides
In the very same way, the user access point to Ocean Tides Coefficients is the OceanTidesCoefficientsFactory which automatically detects available files and uses the adequate loader. If no file is specified by the user, this factory uses the first available file. The loaded data can then be used by the OceanTides model.
// Directory containing the file fes2004_gr final File tiDir = new File("/my/data/gravity/tides"); // The directory is given to the Orekit data loader DataProvidersManager.getInstance().addProvider(new DirectoryCrawler(tiDir)); // The FES2004 file is registered in the OceanTidesCoefficientsFactory OceanTidesCoefficientsFactory.addOceanTidesCoefficientsReader(new FES2004FormatReader("fes2004_gr")); // A provider for the FES2004 data is created final OceanTidesCoefficientsProvider provider = OceanTidesCoefficientsFactory.getCoefficientsProvider(); // Get the C± ans S± coefficients and C± and ε± for a given Doodson number final double doodson = 65.555; final int order = 2; final int degree = 1; final double[] CS = provider.getCpmSpm(doodson, order, degree); final double[] CE = provider.getCpmEpm(doodson, order, degree);
The OceanTides uses a OceanTidesDataProvider which uses itself a OceanTidesCoefficientsProvider, such as the FES 2004 format reader class, and calls the getCpmSpm(double, double, double) methods internally. When the user has created an instance of the OceanTidesDataProvider class, he can pass it on to the constructor of OceanTides, like so :
final Frame earthFrame = FramesFactory.getITRF(); final double earthRadius = 6378136.; final double mu = Constants.EIGEN5C_EARTH_MU; final double density = 1025; final int degree = 10; final int order = 10; final boolean ignoreSecondaryWaves = true; final OceanTidesCoefficientsProvider coefficientsProvider = OceanTidesCoefficientsFactory.getCoefficientsProvider(); final TidesStandard convention = TidesStandard.GINS2004; final OceanTidesDataProvider dataProvider = new OceanTidesDataProvider(coefficientsProvider, convention); final OceanTides tides = new OceanTides(earthFrame, earthRadius, mu, density, degree, order, ignoreSecondaryWaves, dataProvider);
The TerrestrialTides uses a TerrestrialTidesDataProvider. When the user has created an instance of the TerrestrialTidesDataProvider class, he can pass it on to the constructor of OceanTides, like so :
final List<CelestialBody> bodies = new ArrayList<CelestialBody>(); bodies.add(CelestialBodyFactory.getSun()); bodies.add(CelestialBodyFactory.getMoon()); final TerrestrialTides terrestrialTides = new TerrestrialTides(earthFrame, earthRadius, mu, bodies, false, false, false, new TerrestrialTidesDataProvider());
Drag force
Before implementing the drag force, one has to define a vehicle with aerodynamic properties. To do so, it is advised to consult the page about [SPC_FORCES_Home assembly models for force models]. Given an assembly with the right aerodynamic properties, the user can create an instance of AeroModel or DragLiftModel, and use it to create an instance of DragForce :
// sun ephemerides CelestialBodyFactory.clearCelestialBodyLoaders(); final JPLEphemeridesLoader loader = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.SUN); final JPLEphemeridesLoader loaderEMB = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.EARTH_MOON); final JPLEphemeridesLoader loaderSSB = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.SOLAR_SYSTEM_BARYCENTER); CelestialBodyFactory.addCelestialBodyLoader(CelestialBodyFactory.EARTH_MOON, loaderEMB); CelestialBodyFactory.addCelestialBodyLoader(CelestialBodyFactory.SOLAR_SYSTEM_BARYCENTER, loaderSSB); loader.loadCelestialBody(CelestialBodyFactory.SUN); final PVCoordinatesProvider sun = CelestialBodyFactory.getSun(); // DTM2000 atmosphere final Frame itrf = FramesFactory.getITRF(); final OneAxisEllipsoid earth = new OneAxisEllipsoid(6378136.460, 1.0 / 298.257222101, itrf); SolarActivityDataFactory.addSolarActivityDataReader(new ACSOLFormatReader( SolarActivityDataFactory.ACSOL_FILENAME)); final SolarActivityDataProvider data = SolarActivityDataFactory.getSolarActivityDataProvider(); final DTM2000SolarData in = new DTM2000SolarData(data); earth.setAngularThreshold(1e-10); final DTM2000 atm = new DTM2000(in, sun, earth); // aero model of the assembly final AeroModel model = new AeroModel(createAssemblyWithAeroProperties()); // force final ForceModel drag = new DragForce(atm, model);
The implementation of the DragForce class allows at construction to take in account a multiplicative coefficient on the drag acceleration.
Let k be this coefficient, then the attribute k instance of IParamDiffFunction can be instantiated in the following constructors :
// Simple constructor with multiplicative factor k = 1.0 public DragForce(final Atmosphere atmosphere, final DragSensitive spacecraft) // Constructor for k being a double public DragForce(final double k, final Atmosphere atmosphere, final DragSensitive spacecraft) // Constructor for k being a Parameter public DragForce(final Parameter k, final Atmosphere atmosphere, final DragSensitive spacecraft) // General constructor for k being an IParamDiffFunction // This constructor is called by the others public DragForce(final IParamDiffFunction k, final Atmosphere atmosphere, final DragSensitive spacecraft)
In the main constructor, the derivable parameters of function k are stored in the jacobians parameters list the via the method
addJacobiansParameter , the other in the parameters list via addParameter .
Partial derivatives
The drag force model allows the user to compute the partial derivatives of the atmospheric drag acceleration, only for a spherical spacecraft; the available derivatives are the following:
- with respect to the spacecraft position in the inertial frame;
- with respect to the spacecraft velocity in the inertial frame;
- with respect to the drag coefficient (Cx);
- with respect to parameters of function k which are derivable.
Partial derivatives with respect to spacecraft position
Concerning the derivatives with respect to position, their default value is set to zero. This choice has been made because the exact equations to compute them require the derivative of the atmospheric density with respect to the altitude [math]\frac{\partial \rho }{\partial h}[/math], which is not easily available.
Another set of approximated equations to compute the partial derivatives with respect to position has been implemented; these equations do not need the [math]\frac{\partial \rho }{\partial h}[/math] term, but the scale factor [math]\beta[/math]:
[math]\frac{\partial \frac{\partial^{2} {x}_{p}}{\partial {t}^{2}}}{\partial {x}_{p}}=-\frac{\beta {x}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{x}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {x}_{p}}{\partial {t}^{2}}}{\partial {y}_{p}}=-\frac{\beta {y}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{x}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {x}_{p}}{\partial {t}^{2}}}{\partial {z}_{p}}=-\frac{\beta {z}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{x}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {y}_{p}}{\partial {t}^{2}}}{\partial {x}_{p}}=-\frac{\beta {x}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{y}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {y}_{p}}{\partial {t}^{2}}}{\partial {y}_{p}}=-\frac{\beta {y}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{y}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {y}_{p}}{\partial {t}^{2}}}{\partial {z}_{p}}=-\frac{\beta {z}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{y}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {z}_{p}}{\partial {t}^{2}}}{\partial {x}_{p}}=-\frac{\beta {x}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{z}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {z}_{p}}{\partial {t}^{2}}}{\partial {y}_{p}}=-\frac{\beta {y}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{z}_{p}}{\partial {t}^{2}}[/math];
[math]\frac{\partial \frac{\partial^{2} {z}_{p}}{\partial {t}^{2}}}{\partial {z}_{p}}=-\frac{\beta {z}_{p}}{\sqrt{{{x}_{p}}^{2}+{{y}_{p}}^{2}+{{z}_{p}}^{2}}} \frac{\partial^{2}{z}_{p}}{\partial {t}^{2}}[/math];
To use these equations, the user should initialise the value of [math]\beta[/math], which is contained in the AeroSphereProperty class.
The following lines show how to set the proper configuration in order to compute the derivatives using the previous equations:
// create the spherical spacecraft: final AssemblyBuilder builder = new AssemblyBuilder(); // add main part (one sphere) builder.addMainPart("MAIN_BODY"); // sphere property final double radius = 10.; final double cx = 2.; final AeroSphereProperty asp = new AeroSphereProperty(radius, AeroSphereProperty.STANDARD_SCALE_HEIGHT, cx); builder.addProperty(asp, "MAIN_BODY"); // adding aero properties // one facet final Vector3D normal = Vector3D.PLUS_J; final double area = 10.; final Facet facet = new Facet(normal, area); // aero facet property final double cn = 2., ct = 1.; final IPartProperty aeroFacetProp = new AeroFacetProperty(facet, cn, ct); builder.addProperty(aeroFacetProp, "MAIN_BODY"); // adding mass properties final IPartProperty massMainProp = new MassProperty(100.); builder.addProperty(massMainProp, "MAIN_BODY"); // assembly creation final Assembly assembly = builder.returnAssembly(); final AeroModel aeroModel = new AeroModel(assembly); // create the atmosphere: final double ae = Constants.GRIM5C1_EARTH_EQUATORIAL_RADIUS; final Atmosphere atmosphere = new SimpleExponentialAtmosphere( new OneAxisEllipsoid(ae, 1.0 / 298.257222101, FramesFactory.getITRF()), 0.0004, 42000.0, 7500.0); // create the drag force: final DragForce force = new DragForce(atmosphere, aeroModel);
When the AeroSphereProperty instance is initialized without the value of the atmospheric scale height, the derivatives with respect to position are always equal to zero:
final AeroSphereProperty asp = new AeroSphereProperty(radius, cx);
NB: the atmospheric scale height depends on the altitude, but in the Patrius implementation is a constant : for this reason, the result of these equations will be more precise when the orbit is circular. It is suggested not to use them when the considered orbit is highly excentric.
Partial derivatives with respect to spacecraft velocity
The partial derivatives of the drag force with respect to the spacecraft velocity in the inertial frame are computed using the exact equations.
Partial derivatives with respect to the drag coefficient (Cx)
The partial derivatives of the drag force with respect to the drag coefficient are computed using the exact equations.
Note that the ballistic coefficient for a spherical spacecraft is equal to [math]{B}_{c}=\frac{S {C}_{X}}{M}[/math], where [math]S[/math] is the cross-sectional area of the sphere, [math]{C}_{X}[/math] is the drag coefficient and [math]M[/math] is the mass.
Partial derivatives with respect to k parameters
The partial derivatives of the drag force with respect to k parameters are simply computed by multiplying the drag acceleration by the partial derivative value of k with respect to the considered parameter.
Solar radiation pressure
Before implementing the solar radiation pressure or the rediffused solar radiation pressure, one has to define a vehicle with radiative properties. To do so, it is advised to consult the page about forces models using the assembly.
Direct solar radiation pressure
Solar radiation pressure with circular occulting body
Example for the solar radiation pressure implementation :
// Earth equatorial radius from grim4s4_gr GRGS file final double requa = 6378136.0; // dRef reference distance for the solar radiation pressure (m) final double dRef = 149597870000.0; // pRef reference solar radiation pressure at dRef (N/m2) final double pRef = 4.5605E-6; // mass of the spacecraft final double mass = 1000.; // set up JPL ephemeris for the Sun final JPLEphemeridesLoader loader_sun = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.SUN); final CelestialBody sun = loader_sun.loadCelestialBody(CelestialBodyFactory.SUN); // build the assembly final AssemblyBuilder builder = new AssemblyBuilder(); ... final Assembly assembly = builder.returnAssembly(); final RadiationSensitive radiativeModel = new DirectRadiativeModel(assembly); // SRP final SolarRadiationPressure SRP = new SolarRadiationPressure(dRef, pRef, sun, requa, radiativeModel );
Solar radiation pressure with ellipsoid occulting body
Before implementing the solar radiation pressure (that takes into account Earth flattening), one has to define a vehicle with radiative properties. To do so, it is advised to consult the page which describes how to build and use the Assembly (see also...).
The following code snippet allows the user to create an instance of the ForceModel class that can be passed to the NumericalPropagator. This instance will calculate the SRP by computing penumbra and umbra events for a flattened Earth.
// Constants final double ae = 6.3781360000000000E+06; final double f = 3.3528040724231161E-03; // ITRF frame final Frame itrf = FramesFactory.getITRF(); // Sun and Earth final CelestialBody sun = CelestialBodyFactory.getSun(); final GeometricBodyShape earth = new ExtendedOneAxisEllipsoid(ae, f, itrf, "earth"); // Assembly definition final AssemblyBuilder builder = new AssemblyBuilder(); final String mainPart = "satellite"; builder.addMainPart(mainPart); builder.addProperty(new RadiativeProperty(1, 0, 0), mainPart); builder.addProperty(new MassProperty(mass), mainPart); builder.addProperty(new RadiativeSphereProperty(1), mainPart); // The RadiationSensitive instance final DirectRadiativeModel sc = new DirectRadiativeModel(builder.returnAssembly()); // SRP srp = new PatriusSolarRadiationPressure(sun, earth, sc);
Rediffused solar radiation pressure
Example for the rediffused solar radiation pressure implementation :
// sun ephemerides CelestialBodyFactory.clearCelestialBodyLoaders(); final JPLEphemeridesLoader loader = new JPLEphemeridesLoader("unxp2000.405", JPLEphemeridesLoader.EphemerisType.SUN); final CelestialBody sun = loader.loadCelestialBody(CelestialBodyFactory.SUN); // emissivity model final IEmissivityModel modelE = new KnockeRiesModel(); // build the assembly final AssemblyBuilder builder = new AssemblyBuilder(); . . . final Assembly assembly = builder.returnAssembly(); // RSRP model (albedo=true/false, ir=true/false, albedo global multiplicative factor=1, //infrared global multiplicative factor=1 final RediffusedRadiativeModel RSRP = new RediffusedRadiativeModel(albedo, ir, 1, 1, assembly); // RSRP force, number of corona, number of meridian=10 final RediffusedRadiationPressure f = new RediffusedRadiationPressure(sun, FramesFactory.getITRF(), 10, 10, modelE, RSRP);
It is also possible to compute these forces using assemblies, as seen in the spacecraft chapter.
Relativistic Effects
The computation of the relativistic effects is available in PATRIUS, in the force models. The model used to represent these effects is composed of 3 terms :
- the Schwarzschild term, which is the most important
- the Coriolis term, also known as the geodetic precession term
- the Lense-Thirring term, involving the rotation of the considered central body
Three classes (one for each effect) are implemented in the package org.orekit.forces.relativistic of Orekit-addons. The SchwarzschildRelativisticEffect, CoriolisRelativisticEffect, and LenseThirringRelativisticEffect implement the ForceModel and GradientModel interfaces like all force models classes, and extend JacobianParameterizable.
The following sections focus on each relativistic effect.
Implementing the same ForceModel interface, the computation of the acceleration is available via the method computeAcceleration(final SpacecraftState s).
Also, the computation of the acceleration partial derivatives with respect to state (position and velocity) is available via addDAccDState(final SpacecraftState s, final double[][] dAccdPos, final double[][] dAccdVel).
The computation of partial derivatives with respect to parameters in addDAccDParam(final SpacecraftState s, final Parameter param, final double[] dAccdParam) raise an exception since no parameter is supported by these force models.
Schwarzschild effect
An instance of the class SchwarzschildRelativisticEffect can be created using one of the following constructor:
public SchwarzschildRelativisticEffect(final double mu, final boolean computePartialDerivativesPos, final boolean computePartialDerivativesVel)
public SchwarzschildRelativisticEffect(final double mu)
where mu is the central attraction coefficient, the boolean allowing the computation (or not) of the partial derivatives. In the second constructor, booelan are set to true.
The acceleration due to the Schwarzschild effect is analytically computed using the formula:
[math]\vec{a}_{sch} = \frac{\mu} {c^{2} r^{3}} ((4 \frac{{\mu}}{r}- v^{2}) \vec{r} + 4 (\vec{v}.\vec{r}) \vec{v})[/math]
where :
- [math]\vec{r}[/math] is the spacecraft position in an inertial centered central body frame
- [math]\vec{v}[/math] is the spacecraft velocity in an inertial centered central body frame
- [math]\mu[/math] is the attraction coefficient of the central body [math](m^3 s^{-2})[/math]
- [math]c[/math] the constant speed of light
The partial derivatives with respect to state are computed with the following formulae :
[math](\frac{\partial a_{i,sch}}{\partial r_j})_{1 \leq i,j \leq 3} = \frac{-3 r_j}{r^2} a_{i,sch} + \frac{\mu} {c^{2} r^{3}} (\frac{-4 \mu r_j}{r^3} r_i + (4 \frac{\mu}{r}- v^2) \delta_{ij} + 4 v_j v_i)[/math]
[math](\frac{\partial a_{i,sch}}{\partial v_j})_{1 \leq i,j \leq 3} = \frac{\mu} {c^{2} r^{3}} (-2 v_j r_i + 4 r_j v_i + 4 (\vec{v}.\vec{r}) \delta_{ij})[/math]
[math]\delta_{ij}[/math] being the Kronecker symbol.
Coriolis effect
An instance of the class CoriolisRelativisticEffect can be created using one of the following constructor:
public CoriolisRelativisticEffect(final double muSun, final PVCoordinatesProvider sun, final boolean computePartialDerivativesVel)
public CoriolisRelativisticEffect(final double muSun, final PVCoordinatesProvider sun)
where
- muSun is the central attraction coefficient of the Sun
- sun represent the sun PV coordinates in an inertial body centered frame
- axis is an orthogonal axis to the ecliptic plane of the body.
In the second constructor, booelan is set to true.
The acceleration due to the Coriolis effect is analytically computed using the formula:
[math]\vec{a}_{cor} = 2 \vec{\Omega}_{cor} \times \vec{v}[/math]
with :
- [math]\mu_{Sun}[/math] the attraction coefficient of the Sun
- [math]{r}_{body/Sun}[/math] the distance between Sun and the central body
- [math]\vec{u}_{z,ecl}[/math] the normal axis to the ecliptic plane of the body
[math]\vec{\Omega}_{cor} = \frac{-3}{2} \frac{\mu_{Sun}}{c^2 {r^3}_{Sun}} (\vec{v}_{Sun} \times \vec{r}_{Sun})[/math]
Note that this formula for [math]\vec{\Omega}_{cor}[/math] is valid for a IERS2003 model.
with :
- [math]\vec{r}_{Sun}[/math] the position of the Sun in an inertial body centered frame
- [math]\vec{v}_{Sun}[/math] the velocity of the Sun in an inertial body centered frame
The partial derivatives with respect to velocity are computed with the following formula :
[math](\frac{\partial a_{i,cor}}{\partial v_j})_{1 \leq i,j \leq 3} = 2 \left( \begin{array}{ccc} 0 &-\Omega_{cor,3} & \Omega_{cor,2} \\ \Omega_{cor,3} & 0 &-\Omega_{cor,1} \\ -\Omega_{cor,2} & \Omega_{cor,1} & 0 \end{array} \right)[/math]
if we denote [math]\vec{\Omega}_{cor} = (\Omega_{cor,1} \hspace{0.4cm} \Omega_{cor,2} \hspace{0.4cm} \Omega_{cor,3})^T[/math]. We show easily that the derivatives with respect to the position are null.
Lense-Thirring effect
An instance of the class LenseThirringRelativisticEffect can be created using one of the following constructor:
public LenseThirringRelativisticEffect(final double mu, final Frame frame, final boolean computePartialDerivativesPos, final boolean computePartialDerivativesVel)
public LenseThirringRelativisticEffect(final double mu, final Frame frame)
where
- mu is the central attraction coefficient
- frame defines pole of the central body
In the second constructor, booelan are set to true.
The acceleration due to the Lense-Thirring effect is analytically computed using the formula (IERS 20003 standard):
[math]\vec{a}_{LT} = 2 \frac{\mu}{c^2 r^3} (\frac{3}{r^2} (\vec{r}.\vec{J}) \vec{r}- \vec{J}) \times \vec{v}[/math]
where :
- [math]\vec{J} = 9.8* 10^8 \hspace{0.4cm} \vec{u}_{z,Earth}[/math] is the Earth angular momentum.
Finally, the partial derivatives are computed with the following formulae:
[math](\frac{\partial a_{i,LT}}{\partial r_j})_{1 \leq i,j \leq 3} = \frac{-3 r_j}{r} a_{i,LT} + \frac{6 \mu} {c^2 r^5} ((J_j- \frac{2 r_j} {r^2} (\vec{r}.\vec{J})) (\vec{r} \times \vec{v})_i + (\vec{r}.\vec{J}) \frac{\partial}{\partial r_j} (\vec{r} \times \vec{v})_i)[/math]
[math](\frac{\partial a_{i,LT}} {\partial v_j})_{1 \leq i,j \leq 3} = \left( \begin{array}{ccc} 0 &-\Omega_{LT,3} & \Omega_{LT,2} \\ \Omega_{LT,3} & 0 &-\Omega_{LT,1} \\ -\Omega_{LT,2} & \Omega_{LT,1} & 0 \end{array} \right)[/math]
where
[math](\frac{\partial}{\partial r_j} (\vec{r} \times \vec{v})_i)_{1 \leq i,j \leq 3} = \left( \begin{array}{ccc} 0 & v_3 &-v_2 \\ -v_3 & 0 &-v_1 \\ v_2 & v_1 & 0 \end{array} \right)[/math]
and [math]\Omega_{LT} = \frac{\mu}{c^2 r^3} ( \frac{3}{r^2}(\vec{r}.\vec{J}) \vec{r}- \vec{J})[/math]
Thrust
Thrust models include:
- Constant thrust maneuver
- Variable thrust maneuver
- Constant thrust error
Note that impulse thrust are defined as events.
Variable thrust maneuver
The VariableThrustManeuver class implements the ForceModel interface like the ConstantThrustManeuver class; the difference between the two is that the thrust, the ISP and the acceleration direction are constant values in ConstantThrustManeuver, while in VariableThrustManeuver they are represented by the following interfaces: IDependentVariable<SpacecraftState> (thrust and ISP) and IDependentVectorVariable<SpacecraftState> (acceleration direction): this way the algorithms describing the three parameters can be customized.
Constant thrust error
The ConstantThrustError class implements the ForceModel interface like the ConstantThrustManeuver class. The constant thrust error model is a fictitious force model used to compute the difference between the expected maneuver and the actual one. The user defines the three functions representing the three components (x, y, z) of the error as well as the thrust start and end (which can be defined either by its start date and its duration or using event detectors). These functions can depend on parameters. Thrust start and stop criterion can be defined in two different ways (see below).
Being a force model, an acceleration value (the error value) can be computed at any date. Moreover, the partial derivatives of the error at any date with respect to the parameters are available via the method computeDerivative(SpacecraftState, Parameter)
Here is an example of how to define a constant thrust error model:
AbsoluteDate date = new AbsoluteDate(2005, 03, 01, TimeScalesFactory.getTAI()); double duration = 360; Parameter ax = new Parameter("ax", 1.e-12); Parameter ay = new Parameter("ay", 2.e-12); Parameter az = new Parameter("az", 3.e-12); Parameter bx = new Parameter("bx", 4.e-12); Parameter by = new Parameter("by", 5.e-12); Parameter bz = new Parameter("bz", 6.e-12); Parameter cx = new Parameter("cx", 7.e-12); Parameter cy = new Parameter("cy", 8.e-12); Parameter cz = new Parameter("cz", 9.e-12); IParamDiffFunction fx = new QuadraticFunction(date, ax, bx, cx); IParamDiffFunction fy = new QuadraticFunction(date, ay, by, cy); IParamDiffFunction fz = new QuadraticFunction(date, az, bz, cz); ConstantThrustError error = new ConstantThrustError(date, duration, LOFType.TNW, fx, fy, fz);
Maneuver start and stop criterion can either be defined:
◦ With a start date and a duration (former method)
◦ With event detectors, first detector for starting the thrust, second detector for stopping the thrust. Action.STOP is required to trigger (start/stop) the thrust. Any other action will be discarded.
When using event detectors, pay attention to events that may occur several times. If you want the thrust to perform only once, the event detectors the event detectors have to be included in a nth occurrence detector or its shouldBeRemoved() method have to return true. Otherwise the thrust may be performed more than once: if a thrust starts at the perigee (using a perigee detector) and stops at the apogee (using an apogee detector), then the thrust will start at every perigee and stop at every apogee.
Empirical force
The EmpiricalForce class provides a model describing a generic empirical force; an empirical force is a "pseudo acceleration" with the same frequency of the spacecraft orbital frequency (or a multiple of this frequency). One or more instances of this force can be added to a propagator in order to represent a more complex empirical force model.
Given a local frame (usually a LOF frame), and three vectors A, B and C defined in this frame, the acceleration in this local frame due to empirical force is the following:
[math]\overrightarrow{a}_{local}=\overrightarrow{A}\cos(n\omega t) + \overrightarrow{B}\sin(n\omega t) + \overrightarrow{C}[/math]
n is the harmonic factor and [math]\omega[/math] is the orbital period.
As [math]\omega[/math] is usually unknown, [math]\cos(n\omega t)[/math] and [math]\sin(n\omega t)[/math] are computed from the orbital position of the spacecraft:
- when the orbit is highly inclined, the orbital position can be computed from the position of the ascending node;
- when the orbit is heliosyncronous, the orbital position can be computed from the projection of the Sun in the orbital plane;
The user is free to choose a reference vector [math]\overrightarrow{S}[/math] that, once projected in the orbital plane, defines a reference direction used to compute the spacecraft position and then [math]\cos(n\omega t)[/math] and [math]\sin(n\omega t)[/math].
Components of the vectors A, B and C can be defined as parameter and/or parameterizable functions :
final int harmoCoef = 1; EmpiricalForce f = new EmpiricalForce(harmoCoef, Vector3D.PLUS_K, new LinearFunction(new AbsoluteDate(), new Parameter("ax", 1), new Parameter("bx", 2)), new ConstantFunction(new Parameter("ay", 1)), new ConstantFunction(new Parameter("az", 0)), new LinearFunction(new AbsoluteDate(), new Parameter("by", 1), new Parameter("b", 2)), new ConstantFunction(new Parameter("by", 1)), new ConstantFunction(new Parameter("bz", 0)), new LinearFunction(new AbsoluteDate(), new Parameter("bz", 1), new Parameter("b", 2)), new ConstantFunction(new Parameter("cy", 1)) , new ConstantFunction(new Parameter("cz", 0)), LOFType.TNW);
Getting Started
Forces in Orekit implement the ForceModel interface (true for all forces except ImpulseManeuver). They are intended to be used with the NumericalPropagator. The addForceModel(ForceModel) will add a ForceModel to the list of forces the propagator uses at each step.
The simplest way to include a force in the dynamic model is to make an instance of it and to add it to the propagator. Given a ForceModel force, one can use the following code :
myPropagator.addForceModel(force);
Please refer to the Modèle:SiteLink label="Propagation tutorial" jd="OR" suffix="tutorial/propagation.html"/ for more information.
Nota : The ImpulseManeuver force does not implement the ForceModel interface. It implements the EventDetector and should be handled as such (see code below). For more information about Events, please refer to the [MIS_EVT_Home Events section].
myPropagator.addEventDetector(myImpulse);
Important note: forces implement also the GradientModel necessary to provide partial dérivatives computation information. If creating a force model and wishing to compute partial dérivatives, the created force should both inherit ForceModel and GradientModel.
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| ForceModel | This interface represents a force modifying spacecraft motion. | ... |
| GradientModel | This interface provides information about partial dérivatives computation. | ... |
| AttractionModel | This interface represents a gravitational attraction force model. | ... |
| RadiationSensitive | This interface is used to provide an direct solar radiative pressure model. | ... |
| RediffusedRadiationSensitive | This interface is used to provide an rediffused radiative pressure model. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| DragForce | Atmospheric drag force model. | ... |
| EarthGravitationalModelFactory | Factory to provide earth gravitational model. | ... |
| CunninghamAttractionModel | This class represents the gravitational field of a celestial body. It uses unnormalized zonal, tesseral and sectorial coefficients. | ... |
| DrozinerAttractionModel | This class represents the gravitational field of a celestial body. It uses unnormalized zonal, tesseral and sectorial coefficients. | ... |
| BalminoAttractionModel | This class represents the Balmino attraction model of a gravitational field of a celestial body. It uses normalized zonal, tesseral and sectorial coefficients. | ... |
| VariablePotentialAttractionModel | This class represents a variable gravity field. It computes a static potential and a time variable potential. | ... |
| NewtonianAttraction | Force model for Newtonian central body attraction. | ... |
| AbstractTides | This class implements the methods for perturbating force due to tides. | ... |
| OceanTides | This class implements the perturbating force due to ocean tides. | ... |
| TerrestrialTides | This class implements the perturbating force due to terrestrial tides. | ... |
| ThirdBodyAttraction | Third body attraction force model. | ... |
| SolarRadiationPressure | Direct solar radiation pressure force model. | ... |
| PatriusSolarRadiationPressure | Direct solar radiation pressure force model, with Earth flattening. | ... |
| RediffusedRadiationPressure | PATRIUS Rediffused solar pressure force model. | ... |
| EmpiricalForce | Empirical force model. | ... |
| ConstantThrustError | Model of the error of a simple maneuver with constant thrust. | ... |
| SchwarzschildRelativisticEffect | This class computes the relativistic Schwarzschild effect. | ... |
| CoriolisRelativisticEffect | This class computes the relativistic Coriolis effect. | ... |
| LenseThirringRelativisticEffect | This class computes the relativistic Lense-Thirring effect. | ... |