« User Manual 3.3 Numerical propagation » : différence entre les versions
| (6 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 35 : | Ligne 35 : | ||
The PATRIUS library offers different propagators : | The PATRIUS library offers different propagators : | ||
* Numerical propagator | * Numerical propagator | ||
* Analytical propagators (Keplerian, Eckstein-Hechler, J2 secular, Lyddane secular and long period) (see [ | * Analytical propagators (Keplerian, Eckstein-Hechler, J2 secular, Lyddane secular and long period) (see [[User Manual 3.3 Analytical propagation|dedicated User Manual]].) | ||
* Analytical 2D propagator (see [ | * Analytical 2D propagator (see [[User Manual 3.3 Analytical propagation|dedicated User Manual]]) | ||
* TLE propagator (Two Line Element) (see [ | * TLE propagator (Two Line Element) (see [[User Manual 3.3 Analytical propagation|dedicated User Manual]]) | ||
* Precomputed ephemeris propagator (see [ | * Precomputed ephemeris propagator (see [[User Manual 3.3 Analytical propagation|dedicated User Manual]]) | ||
* The STELA propagator (see [ | * The STELA propagator (see [[User Manual 3.3 Semi-analytical propagation|dedicated User Manual]]) | ||
=== Partial Derivatives=== | === Partial Derivatives=== | ||
| Ligne 114 : | Ligne 114 : | ||
|[{{JavaDoc3.3}}/org/orekit/propagation/precomputed/IntegratedEphemeris.html ...] | |[{{JavaDoc3.3}}/org/orekit/propagation/precomputed/IntegratedEphemeris.html ...] | ||
|- | |- | ||
|'''SimpleAdditionalStateProvider''' | |'''SimpleAdditionalStateProvider''' | ||
|This class implements AdditionalStateProvider interface. It simply handles a list of dates associated to additional state vectors. For a given date it returns the associated additional state vector or a propagation exception if this date is not found. This class will be basically used with a PVCoordinatePropagator. | |This class implements AdditionalStateProvider interface. It simply handles a list of dates associated to additional state vectors. For a given date it returns the associated additional state vector or a propagation exception if this date is not found. This class will be basically used with a PVCoordinatePropagator. | ||
| Ligne 137 : | Ligne 136 : | ||
See : {{siteLink label="propagation mode description" jd="OR" suffix="architecture/propagation.html"/}}. Note : Two errors are in that tutorial : getITRF2005() was replaced by getITRF(). VisibilityDetector was replaced by VisibilityFromStationDetector | See : {{siteLink label="propagation mode description" jd="OR" suffix="architecture/propagation.html"/}}. Note : Two errors are in that tutorial : getITRF2005() was replaced by getITRF(). VisibilityDetector was replaced by VisibilityFromStationDetector | ||
|= | {| class="wikitable" | ||
| | |- | ||
| | ! scope="col"| Use case | ||
| | ! scope="col"| without dense output | ||
! scope="col"| with dense output | |||
! scope="col"| with event detection | |||
! scope="col"| with step handler | |||
|- | |||
|slave | |||
| + faster than the others since it has no step handler | |||
| - not adapted when it comes to generate a dense output | |||
| + adapted | |||
| - not adapted | |||
|- | |||
|master | |||
| - not really adapted | |||
| - not really adapted (could be adapted with a specific step handler) | |||
| + adapted | |||
| + adapted | |||
|- | |||
|ephemeris generation | |||
| - not really adapted | |||
| + adapted | |||
| + adapted | |||
| - not adapted | |||
|} | |||
| Ligne 157 : | Ligne 178 : | ||
==== Propagation ==== | ==== Propagation ==== | ||
See : [ | See : [[User Manual 3.3 SpacecraftState|SpacecraftState description]] | ||
Numerical propagation can be executed in cartesian, equinoctial, keplerian and circular parameters. By default, equinoctial parameters are used. | Numerical propagation can be executed in cartesian, equinoctial, keplerian and circular parameters. By default, equinoctial parameters are used. | ||
| Ligne 166 : | Ligne 187 : | ||
Here is presented a basic instanciation of the numerical propagator with an input state built from an [{{JavaDoc3.3}}/org/orekit/orbits/Orbit.html orbit] and a [{{JavaDoc3.3}}/org/orekit/propagation/MassProvider.html mass provider]. | Here is presented a basic instanciation of the numerical propagator with an input state built from an [{{JavaDoc3.3}}/org/orekit/orbits/Orbit.html orbit] and a [{{JavaDoc3.3}}/org/orekit/propagation/MassProvider.html mass provider]. | ||
See : [ | See : [[User Manual 3.3 Assemblies in PATRIUS: Building and using an assembly|Building assembly]] | ||
<syntaxhighlight lang="java"> | <syntaxhighlight lang="java"> | ||
| Ligne 334 : | Ligne 355 : | ||
===== Propagation of the attitudes : two possible treatments ===== | ===== Propagation of the attitudes : two possible treatments ===== | ||
To propagate the [{{JavaDoc3.3}}/org/orekit/attitudes/Attitude.html Attitude], two treatments could be applied : | To propagate the [{{JavaDoc3.3}}/org/orekit/attitudes/Attitude.html Attitude], two treatments could be applied : | ||
* compute the attitude with an [{{JavaDoc3.3}}/org/orekit/attitudes/AttitudeProvider.html AttitudeProvider] : '''''setAttitudeProvider(AttitudeProvider)'''''. | * compute the attitude with an [{{JavaDoc3.3}}/org/orekit/attitudes/AttitudeProvider.html AttitudeProvider] : '''''setAttitudeProvider(AttitudeProvider)'''''.<br>It is possible to deals with : | ||
It is possible to deals with : | ** a single attitude by calling '''''setAttitudeProvider(AttitudeProvider)''''' | ||
** | ** two attitudes by calling '''''setAttitudeProviderForces(AttitudeProvider)''''' or '''''setAttitudeProviderEvents(AttitudeProvider)'''''. It is not possible to call '''''setAttitudeProvider(AttitudeProvider)''''' and '''''setAttitudeProviderForces(AttitudeProvider)''''' (or '''''setAttitudeProviderEvents(AttitudeProvider)''''') | ||
** | * propagate the attitude as a 7-dimension additional state : '''''addAttitudeEquation(AttitudeEquation)'''''.<br>In practical terms, the user has to build the additional equation by extending the abstract class [{{JavaDoc3.3}}/org/orekit/propagation/numerical/AttitudeEquation.html AttitudeEquation], call '''''addAttitudeEquation(AttitudeEquation)'''''. The additional state corresponding with the attitude is automatically add to the additional states map of the initial SpacecraftState. An AttitudeEquation is associated with an AttitudeType : | ||
* propagate the attitude as a 7-dimension additional state : '''''addAttitudeEquation(AttitudeEquation)'''''. | |||
In practical terms, the user has to build the additional equation by extending the abstract class [{{JavaDoc3.3}}/org/orekit/propagation/numerical/AttitudeEquation.html AttitudeEquation], call '''''addAttitudeEquation(AttitudeEquation)'''''. The additional state corresponding with the attitude is automatically add to the additional states map of the initial SpacecraftState. An AttitudeEquation is associated with an AttitudeType : | |||
** ATTITUDE : if a single attitude treatment is done. If the user wants to propagate only one attitude. | ** ATTITUDE : if a single attitude treatment is done. If the user wants to propagate only one attitude. | ||
** ATTITUDE_FORCES and ATTITUDE_EVENTS : if a double attitude treatment is done. If the user wants to propagate the attitude for forces computation and the attitude for events computation. See : [ | ** ATTITUDE_FORCES and ATTITUDE_EVENTS : if a double attitude treatment is done. If the user wants to propagate the attitude for forces computation and the attitude for events computation. See : [[User Manual 3.3 SpacecraftState|SpacecraftState description]] | ||
It is not possible to add an attitude equation in type ATTITUDE and one in type ATTITUDE_FORCES or ATTITUDE_EVENTS. | It is not possible to add an attitude equation in type ATTITUDE and one in type ATTITUDE_FORCES or ATTITUDE_EVENTS. | ||
| Ligne 378 : | Ligne 397 : | ||
</syntaxhighlight> | </syntaxhighlight> | ||
==== Partial derivatives equations | ==== Partial derivatives equations ==== | ||
OREKIT provides an implementation of the interface "'''''AdditionalEquation'''''". This set of additional equations computes the partial derivatives of the state (orbit) with respect to initial state and force models parameters. | OREKIT provides an implementation of the interface "'''''AdditionalEquation'''''". This set of additional equations computes the partial derivatives of the state (orbit) with respect to initial state and force models parameters. | ||
| Ligne 499 : | Ligne 518 : | ||
Note : the dYdY0 terms are given according to the orbit type known to the propagator. If one wants to compute the partial derivatives with equinoctial parameters, then one should specify it to the propagator first, using the method NumericalPropagator.setOrbitType(OrbitType). Additionally, it is also important to specify the correct orbit position angle type (true, mean or eccentric- if the orbit requires it), using the methods NumericalPropagator.setPositionAngleType(PositionAngle). | Note : the dYdY0 terms are given according to the orbit type known to the propagator. If one wants to compute the partial derivatives with equinoctial parameters, then one should specify it to the propagator first, using the method NumericalPropagator.setOrbitType(OrbitType). Additionally, it is also important to specify the correct orbit position angle type (true, mean or eccentric- if the orbit requires it), using the methods NumericalPropagator.setPositionAngleType(PositionAngle). | ||
== Tutorials == | == Tutorials == | ||
Dernière version du 3 avril 2018 à 14:16
Introduction
Scope
This section describes the numerical propagator provided by the Orekit Library: basic orbit propagation, mass, partial derivatives and additional equations. Analytical propagators are détails in Analytical propagation.
Javadoc
Some of the propagation packages available in the Orekit library are listed here :
| Library | Javadoc |
|---|---|
| Orekit | Package org.orekit.propagation |
| Orekit | Package org.orekit.propagation.numerical |
Links
Other useful links can be found here :
- Modèle:SiteLink label="Propagation architecture description" jd="OR" suffix="architecture/propagation.html"/
- Modèle:SiteLink label="Propagation tutorial" jd="OR" suffix="tutorial/propagation.html"/.
Useful Documents
None as of now.
Package Overview
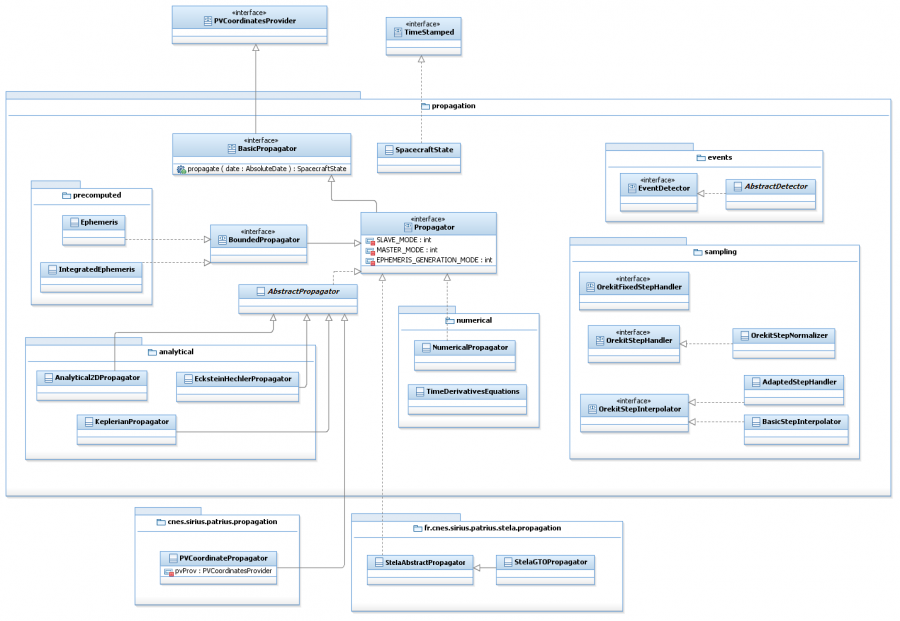
Features Description
Propagators
The PATRIUS library offers different propagators :
- Numerical propagator
- Analytical propagators (Keplerian, Eckstein-Hechler, J2 secular, Lyddane secular and long period) (see dedicated User Manual.)
- Analytical 2D propagator (see dedicated User Manual)
- TLE propagator (Two Line Element) (see dedicated User Manual)
- Precomputed ephemeris propagator (see dedicated User Manual)
- The STELA propagator (see dedicated User Manual)
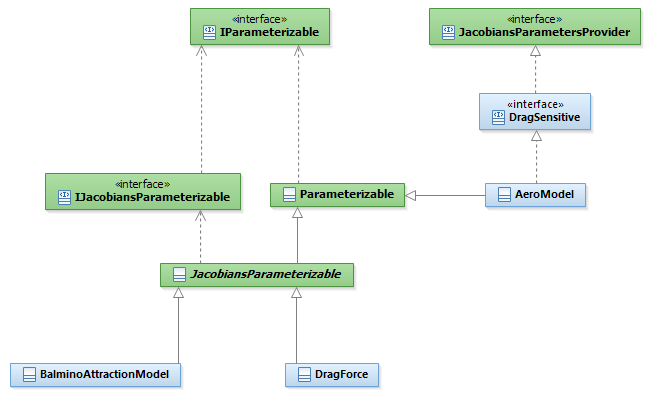
Partial Derivatives
The PATRIUS library offers a comprehensive API that allows computing derivatives using Finite Differences, but also retreiving analytically computed partial derivatives where applicable. The supportParameters() and supportJacobiansParameters() methods from the interfaces given hereunder indicate the user if finite differences and jacobians can be computed.
Getting Started
Modèle:SpecialInclusion prefix=$theme sub section="GettingStarted"/
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| AdditionalStateProvider | This interface represents providers for additional state data beyond SpacecraftState. | ... |
| BoundedPropagator | This interface is intended for ephemerides valid only during a time range. | ... |
| Propagator | This interface provides a way to propagate an orbit at any time. | ... |
Interfaces specific to Numerical propagators
| Interface | Summary | Javadoc |
|---|---|---|
| AdditionalEquations | This interface allows users to add their own differential equations to a numerical propagator. | ... |
| ModeHandler | Common interface for all propagator mode handlers initialization. | ... |
| TimeDerivativesEquations | Interface summing up the contribution of several forces into orbit and mass derivatives. | ... |
Classes
| Class | Summary | Javadoc |
|---|---|---|
| SpacecraftState | This class is the representation of a complete state holding orbit, attitude for forces and for events computation and additional states at a given date. | ... |
| NumericalPropagator | This class propagates SpacecraftState using numerical integration. | ... |
| AttitudeEquation | This class represents attitude differential equations. | ... |
| IntegratedEphemeris | This class stores sequentially generated orbital parameters for later retrieval. | ... |
| SimpleAdditionalStateProvider | This class implements AdditionalStateProvider interface. It simply handles a list of dates associated to additional state vectors. For a given date it returns the associated additional state vector or a propagation exception if this date is not found. This class will be basically used with a PVCoordinatePropagator. | ... |
Using the Propagators
For more information about the propagators of Orekit, please refer to the Modèle:SiteLink label="propagation architecture description" jd="OR" suffix="architecture/propagation.html"/ and the Modèle:SiteLink label="propagation tutorial" jd="OR" suffix="tutorial/propagation.html"/.
Propagation mode
There are three different propagation modes : slave, master and ephemeris generation.
Set to slave mode, the propagator computes the final orbit for a given date and returns it to the user without any intermediate feedback.
When the user wants to call some specific function at the end of each successful step or at the end of a given fixed step during the integration, the propagator has to be set to master mode and a step handler which represents the specific function has to be designed by the user and given to the propagator.
The ephemeris generation mode is used when the user needs random access to the orbit state at any date after the propagation. Be aware that this mode may be memory intensive since all intermediate results are stored.
See : Modèle:SiteLink label="propagation mode description" jd="OR" suffix="architecture/propagation.html"/. Note : Two errors are in that tutorial : getITRF2005() was replaced by getITRF(). VisibilityDetector was replaced by VisibilityFromStationDetector
| Use case | without dense output | with dense output | with event detection | with step handler |
|---|---|---|---|---|
| slave | + faster than the others since it has no step handler | - not adapted when it comes to generate a dense output | + adapted | - not adapted |
| master | - not really adapted | - not really adapted (could be adapted with a specific step handler) | + adapted | + adapted |
| ephemeris generation | - not really adapted | + adapted | + adapted | - not adapted |
NB : To get a dense output, the user should not propagate on a series of time intervals to get intermediate results because at the end of any propagation, the last step is likely readjusted to reach exactly the propagation end date. This behavior differs from the expected one : the integrator parametrization is bypassed, this behavior should remain rare.
Propagation frame
Both analytical and numerical propagators are able to propagate orbits which are defined in a not inertial or pseudo-inertial frame.
However, the propagation has to be performed in an inertial frame, as a result:
- If initial state frame is inertial and user did not specify propagation frame, then propagation will be performed in initial state frame
- If initial state frame is not inertial and user did not specify propagation frame, then an exception will be thrown
- If the user specified a propagation frame, then propagation is performed in specified frame, independently of initial state frame
Propagation frame can be specified using method setOrbitFrame(final Frame frame) of propagators.
Propagation
See : SpacecraftState description
Numerical propagation can be executed in cartesian, equinoctial, keplerian and circular parameters. By default, equinoctial parameters are used.
A loss of accuracy occurs when a numerical propagator using a fixed step RK4 integrator propagates a bulletin using cartesian parameters.
Basic propagation
Here is presented a basic instanciation of the numerical propagator with an input state built from an orbit and a mass provider.
See : Building assembly
// Initial orbit
final AbsoluteDate date = new AbsoluteDate(2000, 3, 1, TimeScalesFactory.getTT());
final double mu = Constants.EGM96_EARTH_MU;
final Frame referenceFrame = FramesFactory.getGCRF();
final Orbit orbit = new KeplerianOrbit(7500000, 0.001, 0.40, 0, 0, 0,PositionAngle.MEAN, referenceFrame, date, mu);
// Initial mass provider
final MassProvider massModel = new MassModel(assembly);
// Initial SpacecraftState
final SpacecraftState initialState = new SpacecraftState(orbit, massModel);
// integrator tolerances for the orbital parameters
final double[] vecAbsoluteTolerance = { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8};
final double[] vecRelativeTolerance = { 1e-10, 1e-10, 1e-10, 1e-10, 1e-10, 1e-10};
// integrator and propagator
final FirstOrderIntegrator integrator = new DormandPrince853Integrator(0.01, 500., vecAbsoluteTolerance, vecRelativeTolerance);
final NumericalPropagator p = new NumericalPropagator(integrator);
// Propagate in cartesian parameters
p.setOrbitType(OrbitType.CARTESIAN);
// Initialize state
p.setInitialState(initialState);
// add equations associated with mass model : compulsory if maneuvers are present !!! Mass provider must be mass provider used in force models.
p.setMassProviderEquation(massModel);
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));
Using Dormand-Prince integrators
Adaptive stepsize Dormand-Prince integrators are commonly use in space mechanics. A 5th order and a 8th order Dormand-Prince integrators are available in Commons-Math.
They have the particularity to have an adaptive step size: during the integration, the integrator tries to keep the integration step as large as possible to save some computation time. The integrator computes the integration step to use by estimating the error made compared to a threshold. The smaller the stepsize, the higher the dynamics of the system.
As a result, the user is required to provide the following information:
- The minimum and maximum allowed step size. The minimum step size should be small enough to handle any integration of the user dynamics. The maximum step size should be high enough to reduce computation times when the dynamics is slow.
- The absolute and relative tolérances. These tolerances are used to estimate the current integration step: the integrator reduces the step size until estimated error is below these tolerances. Warning: it does not mean the accuracy of your integration will be below these tolerances! But only that over one integration step, the use of this integrator should not degrade the accuracy of the result more than the fixed tolerance.
As a rule of thumb, the following instantiation is good for orbit dynamics (stepsize in [0.01s, 500s], absolute tolerance being { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8} and relative tolerance being 1e-10:
final double[] vecAbsoluteTolerance = { 1e-5, 1e-5, 1e-5, 1e-8, 1e-8, 1e-8};
final double[] vecRelativeTolerance = { 1e-10, 1e-10, 1e-10, 1e-10, 1e-10, 1e-10};
final FirstOrderIntegrator integrator = new DormandPrince853Integrator(0.01, 500., vecAbsoluteTolerance, vecRelativeTolerance);
When dealing with another dynamics (semi-analytical propagation, etc.), other parameterization may be more suitable.
Alike the code example above, one has to specify in which parameters type the propagation has to be performed, calling setOrbitType(OrbitType) on the propagator (Orbitype.CARTESIAN for cartesian parameters for example).
Important notice
Dormand-Prince integrators (as well as Higham-hall integrator) uses only states whose tolerance has been defined to estimate error and deduce integration step.
Tolerance is defined if not set to [absolute tolerance = +inf, relative tolerance = 0].
By default, tolerances are not set for partial derivatives. As a result, propagation with or without partial dérivatives will return the exact same PV coordinates.
Adding mass to state vector
Mass is a particular additional state, since it is common state in orbital propagation. Propagation with other additional states is detailed in next section.
Including mass states in propagation requires two step:
- Add mass initial states to state vector:
This is performed by providing a MassProvider to the initial SpacecraftState. Mass information is automaticaly stored as additional states of the SpacecraftState.
- Add mass equations to propagator:
For each mass additional state associated with the SpacecraftState, the corresponding additional equation are added to the numerical propagator using setMassProviderEquation(MassProvider). Important notice: this method should be called only once and provided mass provider must be mass provider used in force models for global propagation consistency.
An example using mass propagation is detailed in next section.
Propagation with additional states
It is possible to propagate the complete SpacecraftState including additional states. It could be particularly interesting to propagate additional states if, for example, some other variables need the dynamical spacecraft state to be computed. These additional states are related to differential equations that have to be given to the numerical propagator. They will be integrated with the same integrator scheme as the motion equations and at the same time. It is also possible to define variation tolerance values specifically for each additional state, so that a variable step integrator can take these into account and reduce its step to compute additional states accurately.
In practical terms, the user has to build the additional equation by implementing the interface "AdditionalEquation".
These additional equations are given to the propagator thanks to the following methods :
- addAdditionalEquation(AdditionalEquation)
- addAttitudeEquation(AttitudeEquation) (see next part)
- setMassProviderEquation(MassProvider) (This method should be called only once, see above section)
The initial value of the additional states are stored in the initial SpacecraftState given to the propagator. The method "setAdditionalStateTolerance(String, double[], double[])" may be used to add variation tolerance values (absolute and relative) for the state. An additional equation should be identified by the user in an unequivocal way by a name (String) which is a mandatory attribute. The link between the additional state and the additional equation is done at the beginning of the propagation. At the beginning of the propagation, it is also checked that the additional states size correspond with the additional tolerances fixed in the propagator.
The following example shows how to propagate a SpacecraftState with a mass and one additional state.
// Initial SpacecraftState
SpacecraftState initialState = new SpacecraftState(orbit, massModel);
// add additional state (of size 3) to the SpacecraftState
final String stateName = "state1";
initialState = initialState.addAdditionalState(stateName, new double[]{1., 2., 3.});
// Initialize state
p.setInitialState(initialState);
// add equations associated with mass model (Mass provider must be mass provider used in force models)
p.setMassProviderEquation(massModel);
// add additional equation associated with the additional state
p.addAdditionalEquations(additionalEquation);
// tolerances (of size 3) for the additional state :
final double[] absoluteTol = { 1e-5, 1e-5, 1e-5 };
final double[] relativeTol = { 1e-10, 1e-10, 1e-10 };
p.setAdditionalStateTolerance(stateName, absoluteTol, relativeTol);
// Propagate in cartesian parameters
p.setOrbitType(OrbitType.CARTESIAN);
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));
It is possible to get a feedback of the additional states evolution throughout the propagation. To that purpose, the user should create a step handler which implements the interface "OrekitStepHandler" and set the propagator to "master mode". The main method of the step handler is the method "handleStep(OrekitStepInterpolator, boolean)" which has to be designed by the user according to what he wants to do at the end of each integration step. For example, in order to get a feedback of the additional states once the propagation is performed, the user could design this method in the following manner :
@Override
public void handleStep(final OrekitStepInterpolator interpolator, final boolean isLast)
throws PropagationException {
SpacecraftState currentState;
Map<String, double[]> addStates;
try {
currentState = interpolator.getInterpolatedState();
addStates = currentState.getAdditionalStates();
datesList.add(currentState .getDate());
pv.add(currentState.getPVCoordinates());
addStatesMap.add(currentState.getAdditionalStates());
} catch (OrekitException e) {
e.printStackTrace();
}
}
If you want to keep the provided interpolator for later use, add in handleStep method:
((AdaptedStepHandler) interpolator).copy();
To continue the previous example :
// propagation
final StateObserver stepHandler = new StateObserver();
p.setMasterMode(stepHandler);
p.resetInitialState(new SpacecraftState(orbit));
p.propagate(date.shiftedBy(propagationDuration));
final List<AbsoluteDate> dates = stepHandler.getDatesList();
final List<Double> mass = stepHandler.getAddStateList();
final List<PVCoordinates> pv = stepHandler.getDatesList();
Propagation of the attitudes : two possible treatments
To propagate the Attitude, two treatments could be applied :
- compute the attitude with an AttitudeProvider : setAttitudeProvider(AttitudeProvider).
It is possible to deals with :- a single attitude by calling setAttitudeProvider(AttitudeProvider)
- two attitudes by calling setAttitudeProviderForces(AttitudeProvider) or setAttitudeProviderEvents(AttitudeProvider). It is not possible to call setAttitudeProvider(AttitudeProvider) and setAttitudeProviderForces(AttitudeProvider) (or setAttitudeProviderEvents(AttitudeProvider))
- propagate the attitude as a 7-dimension additional state : addAttitudeEquation(AttitudeEquation).
In practical terms, the user has to build the additional equation by extending the abstract class AttitudeEquation, call addAttitudeEquation(AttitudeEquation). The additional state corresponding with the attitude is automatically add to the additional states map of the initial SpacecraftState. An AttitudeEquation is associated with an AttitudeType :- ATTITUDE : if a single attitude treatment is done. If the user wants to propagate only one attitude.
- ATTITUDE_FORCES and ATTITUDE_EVENTS : if a double attitude treatment is done. If the user wants to propagate the attitude for forces computation and the attitude for events computation. See : SpacecraftState description
It is not possible to add an attitude equation in type ATTITUDE and one in type ATTITUDE_FORCES or ATTITUDE_EVENTS.
The following example shows how to propagate a SpacecraftState with an attitude added to the additional states map.
// Initial SpacecraftState
SpacecraftState initialState = new SpacecraftState(orbit, attitude);
// Initialize state
p.setInitialState(initialState);
// add equation associated with the attitude
p.addAttitudeEquation(new AttitudeEquation(AttitudeType.ATTITUDE) {
public void computeDerivatives(SpacecraftState s, TimeDerivativesEquations adder) throws OrekitException {...}
});
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));
The following example shows how to propagate a SpacecraftState with two attitude (one added to the additional states map, the other computed with the AttitudeProvider).
// Initial SpacecraftState
SpacecraftState initialState = new SpacecraftState(orbit, attitudeForces, attitudeEvents);
// Initialize state
p.setInitialState(initialState);
// add equations associated with attitude for forces computation
p.addAttitudeEquation(new AttitudeEquation(AttitudeType.ATTITUDE_FORCES) {
public void computeDerivatives(SpacecraftState s, TimeDerivativesEquations adder) throws OrekitException {...}
});
// add attitude provider for events computation : attitude law aligned with EME2000
final AttitudeProvider attProv = new ConstantAttitudeLaw(FramesFactory.getEME2000(), Rotation.IDENTITY);
p.setAttitudeProviderEvents(attProv);
// propagation
final SpacecraftState finalState = p.propagate(date.shiftedBy(propagationDuration));
Partial derivatives equations
OREKIT provides an implementation of the interface "AdditionalEquation". This set of additional equations computes the partial derivatives of the state (orbit) with respect to initial state and force models parameters.
This set of equations is automatically added to a numerical propagator in order to compute partial derivatives of the orbit during a propagation. This is useful in orbit determination applications. The force models implement analytical methods to compute partial derivatives with respect to state or force models parameters. If not, the finite difference method is applied.
Partial derivatives with respect to state (position or velocity) can be tuned or disabled:
- They can be disabled for every force inheriting
GradientModelusing the provided constructors. - For potential models (excluding Droziner model), order and degree can be tuned differently for acceleration computation and partial dérivatives computation.
The general principles are described in the above sectionAdditional state. An example is given here to see how to propagate jacobians throughout an orbit. We call dYdY0 the partial derivatives of the state with respect to initial state and dYdP the partial derivatives of the state with respect to force models parameters.
First, the user has to add the partial derivatives equations of the state. Upon construction, this set of equations is automatically added to the propagator by calling its "NumericalPropagator.addAdditionalEquations(AdditionalEquations)" method. So there is no need to call this method explicitly for these equations.
After that, the user has to set the initial value of the jacobians with respect to state and parameters, using the "PartialDerivativesEquations.setInitialJacobians(SpacecraftState, int)" method (or "setInitialJacobians(SpacecraftState, double[][])"). This method is equivalent to call "setInitialJacobians(SpacecraftState, double[][], double[][])" with dYdY0 set to the identity matrix and dYdP set to a zero matrix. Other similar methods are provided if the user wants to specifically set initial Jacobians with respect to state or to one particular parameter ("setInitialJacobians(SpacecraftState, Parameter, double[])".
To use the jacobians, it is necessary to define a mapper between one-dimensional additional state and two-dimensional jacobians.
// we assume that a propagator "propagator" has been built with its initial state "initialState"
// add the partial derivatives of the state with respect to initial state,
// with a name to identify it
final PartialDerivativesEquations partials = new PartialDerivativesEquations("PDE", propagator);
// set the initial value of the jacobians
// here state dimension = 6 and parameter dimension = 0
partials.setInitialJacobians(initialState, 0);
// get a mapper between two-dimensional jacobians and one-dimensional additional state
// with the same name as the instance
final JacobiansMapper mapper = partials.getMapper();
[...]
In order to get the jacobians throughout the propagation, the user can create a step handler which implements the interface "OrekitStepHandler" and set the propagator to "master mode". The example shows how to get jacobians during the propagation. The following class "JacobiansHandler" implements "OrekitStepHandler" (the main methods are given hereafter).
// step handler constructor
public JacobiansHandler(final JacobiansMapper inMapper, final AbsoluteDate inDate) {
this.mapper = inMapper;
this.date = inDate;
dYdY0 = new double[mapper.getStateDimension()][mapper.getStateDimension()];
dYdP = new double[mapper.getStateDimension()][mapper.getParameters()];
}
@Override
public void handleStep(final OrekitStepInterpolator interpolator, final boolean isLast)
throws PropagationException {
try {
if (date == null) {
// we want to pick up the Jacobians at the end of last step
if (isLast) {
// set the interpolated date which is the current grid date (the last step)
interpolator.setInterpolatedDate(interpolator.getCurrentDate());
}
} else {
// we want to pick up some intermediate Jacobians
final double dt0 = date.durationFrom(interpolator.getPreviousDate());
final double dt1 = date.durationFrom(interpolator.getCurrentDate());
if (dt0* dt1 > 0) {
// the current step does not cover the pickup date
return;
} else {
// set the interpolated date
interpolator.setInterpolatedDate(date);
}
}
// get the interpolated state at the current interpolated date
final SpacecraftState state = interpolator.getInterpolatedState();
// get the Jacobian with respect to state-> dYdY0 array
dYdY0 = mapper.getStateJacobian(state);
// get the Jacobian with respect to parameters-> dYdP array
dYdP = mapper.getParametersJacobian(state);
// get the Jacobian with respect to parameter 1-> dYdP1 array
dYdP1 = mapper.getParametersJacobian(parameter1, state);
} catch (PropagationException pe) {
throw pe;
} catch (OrekitException oe) {
throw new PropagationException(oe);
}
}
// Method to get the jacobian with respect to initial state
public double[][] getdYdY0() {
return dYdY0;
}
To continue with the main program, a way to get the jacobians and to use it could be the following:
[...]
// add a step handler to get the jacobian matrix corresponding to the last date
// can be used to get the jacobians corresponding to a given date
final JacobiansHandler jacobiHandler = new JacobiansHandler(mapper, initialDate.shiftedBy(dt));
propagator.setMasterMode(jacobiHandler);
// propagate the orbit until initialDate+dt
final SpacecraftState finalState = propagator.propagate(initialDate.shiftedBy(dt));
// get the jacobian matrix with respect to initial state at the final date
final double[][] dYdY0 = jacobiHandler.getdYdY0();
// examples using jacobians...
// convert dYdY0 into a RealMatrix
final RealMatrix mat = new Array2DRowRealMatrix(dYdY0);
// invert mat, using LU decomposition
final RealMatrix matInverse = new LUDecomposition(mat).getSolver().getInverse();
[...]
Note : the dYdY0 terms are given according to the orbit type known to the propagator. If one wants to compute the partial derivatives with equinoctial parameters, then one should specify it to the propagator first, using the method NumericalPropagator.setOrbitType(OrbitType). Additionally, it is also important to specify the correct orbit position angle type (true, mean or eccentric- if the orbit requires it), using the methods NumericalPropagator.setPositionAngleType(PositionAngle).
Tutorials
Tutorial 1
Modèle:SpecialInclusion prefix=$theme sub section="Tuto1"/
Tutorial 2
Modèle:SpecialInclusion prefix=$theme sub section="Tuto2"/
 Tips & Tricks
Tips & Tricks
| Propagator | Constructor | Comment |
|---|---|---|
| KeplerianPropagator | KeplerianPropagator(Orbit, AttitudeProvider) | This constructor internally creates a SpacecraftState instance with the user specified AttitudeProvider. Note : if the setAttitudeProvider method is used, the initialState is not updated with the new AttitudeProvider. In that case, the user should manually create a new SpacecraftState instance and give it the propagator using the resetInitialState method. Finally, one should not that the standard gravitational parameter and the spacecraft mass are not important here because this propagator will only change the mean anomaly depending on the time elapsed since the orbit date. |
| NumericalPropagator | NumericalPropagator(FirstOrderIntegrator) | After creating the NumericalPropagator instance, the user must provide an initial SpacecraftState. The user can also provide more parameters, such as AttitudeProviders, ForceModels and so on (see javadoc for more details). |