User Manual 4.6 Propagation : Différence entre versions

De Wiki
Aller à : navigation, rechercher
(Page créée avec « == Introduction == === Scope === This section makes a general presentation of propagators : explanations about using them are given with practical examples of use illustr... »)
 
(Aucune différence)

Version actuelle en date du 26 août 2020 à 14:04

Introduction

Scope

This section makes a general presentation of propagators : explanations about using them are given with practical examples of use illustrated by code chuncks.

The PATRIUS library offers different propagators :

Features presented in this section are available to all propagators.

Javadoc

Some of the propagation packages available in the Patrius library are listed here :

Library Javadoc
Patrius Package fr.cnes.sirius.patrius.propagation

Links

None as of now.

Useful Documents

None as of now.

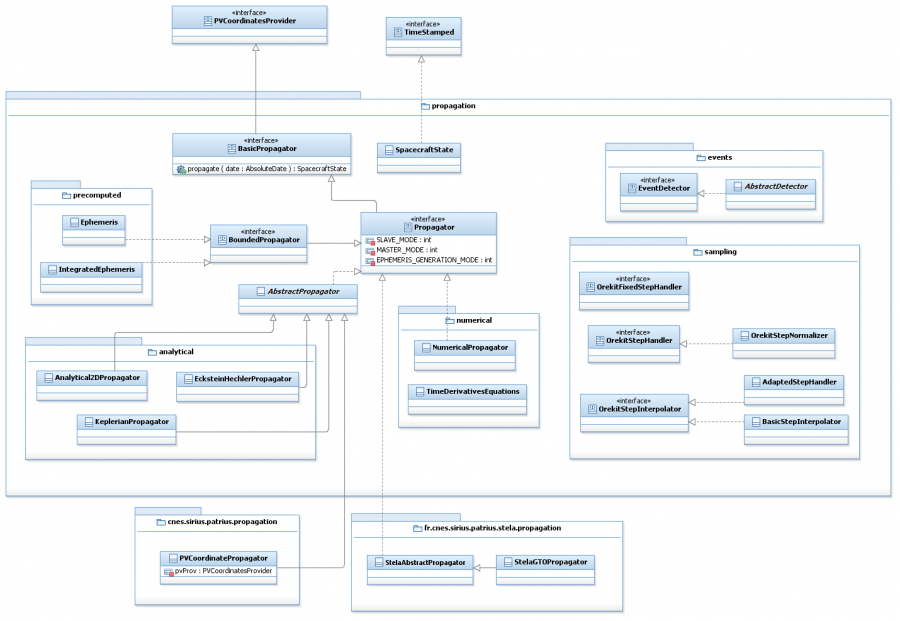
Package overview

Hereunder is given an UML overview of the propagator package :

Propagators2.png

Features description

Propagation mode

There are three different propagation modes : slave, master and ephemeris generation.

Slave mode

Set to slave mode, the propagator computes the final orbit for a given date and returns it to the user without any intermediate feedback.

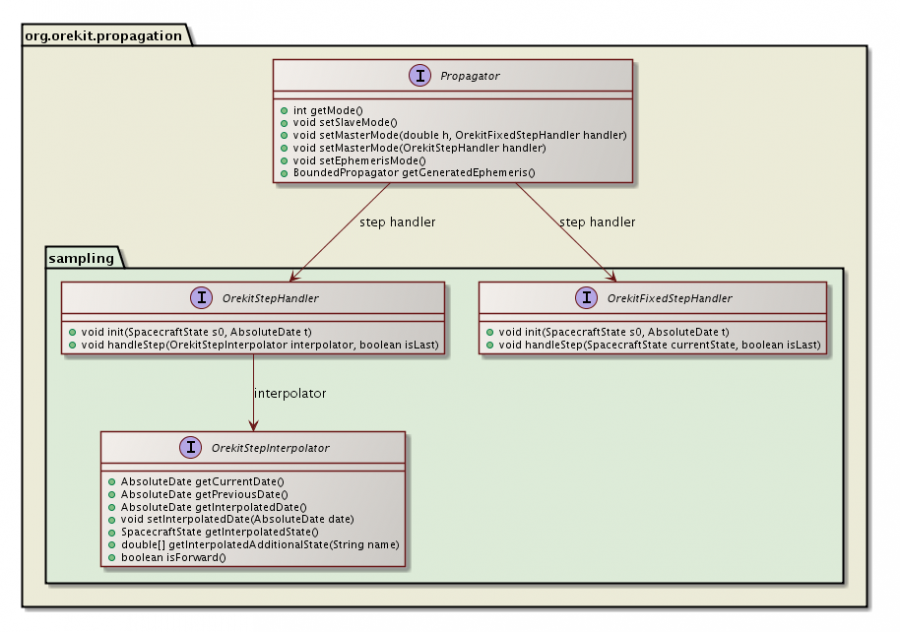
Master mode : using step handlers

When the user wants to call some specific function at the end of each successful step or at the end of a given fixed step during the integration, the propagator has to be set to master mode and a step handler which represents the specific function has to be designed by the user and given to the propagator : the associated method is handleStep(). The package view for step handler classes is presented here :

Sampling-class-diagram.png

To illustrate how to use this mode on a pratical example, let's define some initial state with :

  • an inertial frame
  • a date in some time scale
  • a central attraction coefficient
  • an orbit defined by its keplerian parameters 
// Inertial frame
Frame inertialFrame = FramesFactory.getEME2000();
// Initial date
TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate initialDate = new AbsoluteDate(2004, 01, 01, 23, 30, 00.000,utc);
// Central attraction coefficient
double mu =  3.986004415e+14;
// Initial orbit
double a = 24396159;                // semi major axis in meters
double e = 0.72831215;              // eccentricity
double i = Math.toRadians(7);       // inclination
double omega = Math.toRadians(180); // perigee argument
double raan = Math.toRadians(261);  // right ascention of ascending node
double lM = 0;                      // mean anomaly
Orbit initialOrbit = new KeplerianOrbit(a, e, i, omega, raan, lM, PositionAngle.MEAN, 
                                        inertialFrame, initialDate, mu);
// Initial state definition
SpacecraftState initialState = new SpacecraftState(initialOrbit);

Here we use a more sophisticated NumericalPropagator based on an some adaptive step integrator provided by the math package, but no matter which integrator is used. 

// Adaptive step integrator
// with a minimum step of 0.001 and a maximum step of 1000
double minStep = 0.001;
double maxstep = 1000.0;
double positionTolerance = 10.0;
OrbitType propagationType = OrbitType.KEPLERIAN;
double[][] tolerances =
    NumericalPropagator.tolerances(positionTolerance, initialOrbit, propagationType);
AdaptiveStepsizeIntegrator integrator =
    new DormandPrince853Integrator(minStep, maxstep, tolerances[0], tolerances[1]);

We set up the integrator, and force it to use Keplerian parameters for propagation. 

NumericalPropagator propagator = new NumericalPropagator(integrator);
propagator.setOrbitType(propagationType);

A force model, reduced here to a single perturbing gravity field, is taken into account. More precisions on force models can be found in [ORB_FORCE_Home in Force models page]. 

Frame ITRF = FramesFactory.getITRF(); // terrestrial frame
double ae  =  6378137.;                       // equatorial radius in meter
double c20 = -1.08262631303e-3;               // J2 potential coefficient
 
// potential coefficients arrays (only J2 is considered here)
double[][] c = new double[3][1];
c[0][0] = 0.0;
c[2][0] = c20;
double[][] s = new double[3][1];
ForceModel cunningham = new CunninghamAttractionModel(ITRF, ae, mu, c, s);

This force model is simply added to the propagator: 

propagator.addForceModel(cunningham);

The propagator operating mode is set to master mode with fixed step and a TutorialStepHandler which implements the interface PatriusFixedStepHandler in order to fulfill the handleStep method to be called within the loop. For the purpose of this tutorial, the handleStep method will just print the current state at the moment. 

propagator.setMasterMode(60., new TutorialStepHandler());

Then, the initial state is set for the propagator: 

propagator.setInitialState(initialState);

Finally, the propagator is just asked to propagate, from the initial state, for a given duration. 

SpacecraftState finalState =
    propagator.propagate(new AbsoluteDate(initialDate, 630.));

Clearly, with a few lines of code, the main application delegates to the propagator the care of handling regular outputs through a variable step integration loop.

The only need is to derived some class from the interface PatriusFixedStepHandler to realize a handleStep method, as follows: 

private static class TutorialStepHandler implements PatriusFixedStepHandler {
 
    public void handleStep(SpacecraftState currentState, boolean isLast) {
        System.out.println(" time : " + currentState.getDate());
        System.out.println(" " + currentState.getOrbit());
        if (isLast) {
            System.out.println(" this was the last step ");
        }
    }
}

For the same result, with the slave mode, it would have required much more programming.

The printed results are shown below: 

 time : 2004-01-01T23:30:00.000
 keplerian parameters: {a: 2.4396159E7; e: 0.72831215; i: 7.0; pa: 180.0; raan: 261.0; v: 0.0;}
 time : 2004-01-01T23:31:00.000
 keplerian parameters: {a: 2.439564424480015E7; e: 0.7283054179012741; i: 6.999949573716115; pa: 180.01089879431635; raan: 260.9999744509341; v: 5.270522984259634;}
 time : 2004-01-01T23:32:00.000
 keplerian parameters: {a: 2.4394130981544524E7; e: 0.7282856263106472; i: 6.999800432744152; pa: 180.02168751826343; raan: 260.9997982967906; v: 10.50387496695558;}
 time : 2004-01-01T23:33:00.000
 keplerian parameters: {a: 2.4391710665289845E7; e: 0.7282539637676634; i: 6.999563066306985; pa: 180.03226220891892; raan: 260.99933874845317; v: 15.664604011799053;}
 time : 2004-01-01T23:34:00.000
 keplerian parameters: {a: 2.438852138985819E7; e: 0.7282122258929671; i: 6.9992532645274546; pa: 180.04252939476373; raan: 260.9984960696569; v: 20.720499012905563;}
 time : 2004-01-01T23:35:00.000
 keplerian parameters: {a: 2.438473009191154E7; e: 0.7281625851163973; i: 6.998890000900681; pa: 180.05240967921347; raan: 260.9972118041821; v: 25.643756282394765;}
 time : 2004-01-01T23:36:00.000
 keplerian parameters: {a: 2.4380513619406037E7; e: 0.7281073453198131; i: 6.998493179635541; pa: 180.06183982161005; raan: 260.9954699357843; v: 30.411707875362936;}
 time : 2004-01-01T23:37:00.000
 keplerian parameters: {a: 2.4376042162606522E7; e: 0.7280487266192758; i: 6.998081669198389; pa: 180.0707733525973; raan: 260.9932919569584; v: 35.00709604303499;}
 time : 2004-01-01T23:38:00.000
 keplerian parameters: {a: 2.4371467133870374E7; e: 0.727988707383731; i: 6.997671877833683; pa: 180.07917999091737; raan: 260.99072804117174; v: 39.41795154717632;}
 time : 2004-01-01T23:39:00.000
 keplerian parameters: {a: 2.4366914169719197E7; e: 0.7279289324335715; i: 6.99727695633292; pa: 180.08704419756123; raan: 260.98784670576674; v: 43.63716855903322;}
 time : 2004-01-01T23:40:00.000
 keplerian parameters: {a: 2.436248074752743E7; e: 0.7278706810843818; i: 6.996906568384245; pa: 180.09436319418123; raan: 260.9847250080804; v: 47.66188030915512;}
 this was the last step 
 Final date  : 2004-01-01T23:40:30.000
 Final state : keplerian parameters: {a: 2.4360331834936075E7; e: 0.7278424290862751; i: 6.996732681960374; pa: 180.097820317503; raan: 260.98309840201875; v: 49.6013850854552;}

Ephemeris mode

The ephemeris generation mode is used when the user needs random access to the orbit state at any date after the propagation. Be aware that this mode may be memory intensive since all intermediate results are stored.

To illstrate it, let's also first define some initial state with :

  • an inertial frame
  • a date in some time scale
  • a central attraction coefficient
  • an orbit defined by its keplerian parameters 
// Inertial frame
Frame inertialFrame = FramesFactory.getEME2000();
// Initial date
TimeScale utc = TimeScalesFactory.getUTC();
AbsoluteDate initialDate = new AbsoluteDate(2004, 01, 01, 23, 30, 00.000,utc);
// Central attraction coefficient
double mu =  3.986004415e+14;
// Initial orbit
double a = 24396159;                // semi major axis in meters
double e = 0.72831215;              // eccentricity
double i = Math.toRadians(7);       // inclination
double omega = Math.toRadians(180); // perigee argument
double raan = Math.toRadians(261);  // right ascention of ascending node
double lM = 0;                      // mean anomaly
Orbit initialOrbit = new KeplerianOrbit(a, e, i, omega, raan, lM, PositionAngle.MEAN, 
                                        inertialFrame, initialDate, mu);
// Initial state definition
SpacecraftState initialState = new SpacecraftState(initialOrbit);

Here we use a simple NumericalPropagator, without perturbation, based on a classical fixed step Runge-Kutta integrator provided by the math package. 

double stepSize = 10;
FirstOrderIntegrator integrator = new ClassicalRungeKuttaIntegrator(stepSize);
NumericalPropagator propagator = new NumericalPropagator(integrator);

The initial state is set for this propagator: 

propagator.setInitialState(initialState);

Then, the propagator operating mode is simply set to ephemeris mode: 

propagator.setEphemerisMode();

And the propagation is performed for a given duration. 

SpacecraftState finalState =
    propagator.propagate(new AbsoluteDate(initialDate, 6000));

This finalState can be used for anything, to be printed for example just like below: 

 Numerical propagation :
 Final date : 2004-01-02T01:10:00.000
 equinoctial parameters: {a: 2.4396159E7;
                           ex: 0.11393312156755062; ey: 0.719345418868777;
                           hx: -0.009567941763699867; hy: -0.06040960680288257;
                           lv: 583.1250344407331;}

Throughout the propagation, intermediate states are stored within an ephemeris which can be recovered now just with one instruction: 

BoundedPropagator ephemeris = propagator.getGeneratedEphemeris();
System.out.println(" Ephemeris defined from " + ephemeris.getMinDate() +
                   " to " + ephemeris.getMaxDate());

The ephemeris is defined as a BoundedPropagator, which means that it is valid only between the propagation initial and final dates. The code above give the following result: 

Ephemeris defined from 2004-01-01T23:30:00.000 to 2004-01-02T01:10:00.000

Between these dates, the ephemeris can be used as any propagator to propagate the orbital state towards any intermediate date just with one instruction: 

SpacecraftState intermediateState = ephemeris.propagate(intermediateDate);

Here are results obtained with intermediate dates set to 3000 second after start date and to exactly the final date: 

 Ephemeris propagation :
 date :  2004-01-02T00:20:00.000
 equinoctial parameters: {a: 2.4396159E7;
                           ex: 0.11393312156755062; ey: 0.719345418868777;
                           hx: -0.009567941763699867; hy: -0.06040960680288257;
                           lv: 559.0092657655284;}
  date :  2004-01-02T01:10:00.000
  equinoctial parameters: {a: 2.4396159E7;
                           ex: 0.11393312156755062; ey: 0.719345418868777;
                           hx: -0.009567941763699867; hy: -0.06040960680288257;
                           lv: 583.1250344407331;}

The following shows the error message we get when we try to use a date outside of the ephemeris range (in this case, the intermediate date was set to 1000 seconds before ephemeris start: 

out of range date for ephemerides: 2004-01-01T23:13:20.000

Choosing the suitable mode

Here are given advantages and drawbacks of each mode according the context : be sure to use the suitable one reading it !

Use case without dense output with dense output with event detection with step handler
slave + faster than the others since it has no step handler - not adapted when it comes to generate a dense output + adapted - not adapted
master - not really adapted - not really adapted (could be adapted with a specific step handler) + adapted + adapted
ephemeris generation - not really adapted + adapted + adapted - not adapted

NB : To get a dense output, the user should not propagate on a series of time intervals to get intermediate results because at the end of any propagation, the last step is likely readjusted to reach exactly the propagation end date. This behavior differs from the expected one : the integrator parametrization is bypassed, this behavior should remain rare.

Propagation frame

Both analytical and numerical propagators are able to propagate orbits which are defined in a not inertial or pseudo-inertial frame. However, the propagation has to be performed in an inertial frame, as a result:

  • If initial state frame is inertial and user did not specify propagation frame, then propagation will be performed in initial state frame
  • If initial state frame is not inertial and user did not specify propagation frame, then an exception will be thrown
  • If the user specified a propagation frame, then propagation is performed in specified frame, independently of initial state frame

Propagation frame can be specified using method setOrbitFrame(final Frame frame) of propagators.

Events management

This paragraph aims to show the power and simplicity of the event handling mechanism. One needs to check the visibility between a satellite and a ground station during some time range.
We will use, and extend, the predefined ElevationDetector to perform the task. The goal is not to make a complete presentation of events detectors but to introduce it in the context of propagators :
events detectors are spreadly developped at the [MIS_EVT_Home dedicated Events detection page]. First, let's set up an initial state for the satellite defined by a position and a velocity at one date in some inertial frame. 

Vector3D position  = new Vector3D(-6142438.668, 3492467.560, -25767.25680);
Vector3D velocity  = new Vector3D(505.8479685, 942.7809215, 7435.922231);
PVCoordinates pvCoordinates = new PVCoordinates(position, velocity);
AbsoluteDate initialDate =
    new AbsoluteDate(2004, 01, 01, 23, 30, 00.000, TimeScalesFactory.getUTC());
Frame inertialFrame = FramesFactory.getEME2000();

We also need to set the central attraction coefficient to define the initial orbit as a KeplerianOrbit. 

double mu =  3.986004415e+14;
Orbit initialOrbit =
    new KeplerianOrbit(pvCoordinates, inertialFrame, initialDate, mu);

As a propagator, we consider a KeplerianPropagator to compute the simple keplerian motion. It could be more elaborate without modifying the general purpose of this speech. 

Propagator kepler = new KeplerianPropagator(initialOrbit);

Then, let's define the ground station by its coordinates as a GeodeticPoint: 

double longitude = Math.toRadians(45.);
double latitude  = Math.toRadians(25.);
double altitude  = 0.;
GeodeticPoint station1 = new GeodeticPoint(latitude, longitude, altitude);

And let's associate to it a TopocentricFrame related to a BodyShape in some terrestrial frame. 

double ae =  6378137.0;                // equatorial radius in meter
double f  =  1.0 / 298.257223563;      // flattening
Frame ITRF = FramesFactory.getITRF();  // terrestrial frame at an arbitrary date
BodyShape earth = new OneAxisEllipsoid(ae, f, ITRF);
TopocentricFrame sta1Frame = new TopocentricFrame(earth, station1, "station1");

More precisions on BodyShape and GeodeticPoint can be found in [FDY_BODY_Home Bodies page]. More precisions on TopocentricFrame can be found in [FDY_FRAME_Home Frames page].

An EventDetector is defined as a VisibilityFromStationDetector which is derived from an ElevationDetector with the same specific parameters. 

double maxcheck  = 1.;
double elevation = Math.toRadians(5.);
EventDetector sta1Visi = new VisibilityFromStationDetector(maxcheck, elevation, sta1Frame);

This EventDetector is added to the propagator: 

kepler.addEventDetector(sta1Visi);

Finally, the propagator is simply asked to perform until some final date, in slave mode by default.

It will propagate from the initial date to the first raising or for the fixed duration according to the behavior implemented in the VisibilityDetector class. 

SpacecraftState finalState =
    kepler.propagate(new AbsoluteDate(initialDate, 1500.));

The main application code is very simple, all the work is done inside the propagator thanks to the VisibilityDetector class especially created for the purpose.

This class extends the ElevationDetector class, by overriding the eventOccurred method with the special ability to print the results of the visibility check, both the raising and the setting time, and to stop the propagation just after the setting detection.

The printed result is shown below. We can see that the propagation stopped just after detecting the raising: 

Visibility on station1 begins at 2004-01-01T23:31:52.097
Visibility on station1 ends at 2004-01-01T23:42:48.850
Final state : 2004-01-01T23:42:48.850

Content

Interfaces

Interface Summary Javadoc
BoundedPropagator This interface is intended for ephemerides valid only during a time range. ...
Propagator This interface provides a way to propagate an orbit at any time. ...

Classes

Class Summary Javadoc
SpacecraftState This class is the representation of a complete state holding orbit, attitude for forces and for events computation and additional states at a given date. ...
Récupérée de « http://patrius.cnes.fr/index.php?title=User_Manual_4.6_Propagation&oldid=2770 »