« User Manual 4.15 Semi-analytical propagation » : différence entre les versions
Aucun résumé des modifications |
Aucun résumé des modifications |
||
| Ligne 564 : | Ligne 564 : | ||
|- | |- | ||
|'''MSISE2000''' | |'''MSISE2000''' | ||
|Classe de modélisation pour le modèle d'atmosphère | |Classe de modélisation pour le modèle d'atmosphère MSIS00 (ex MSIS00Adapter du code de STELA). | ||
|[{{JavaDoc4.15}}/fr/cnes/sirius/patrius/forces/atmospheres/MSISE2000.html ...] | |[{{JavaDoc4.15}}/fr/cnes/sirius/patrius/forces/atmospheres/MSISE2000.html ...] | ||
|} | |} | ||
Dernière version du 28 novembre 2024 à 09:35
Introduction
Scope
This section describes the semi-analytical propagator stemming from Stela software. Its propagator and force model will be briefly explained hereafter. Generic features about propagators as well as other type of propagators are detailed [ORB_PGEN_Home here].
Warnings
Assembly
Stela propagator uses Assembly. Beware as the implemented STELA force models are only validated for a spherical spacecraft. Usage of more elaborate assemblies is not validated, and as such, is not guaranteed to provide satisfactory results.
Javadoc
The packages associated to Stela propagator are :
Links
Stela page
Stela Software and its release notes, User Manual and Javadoc can be found following this link :
Contact IF you are experiencing any issue with STELA Library, feel free to contact the STELA team using the email address below:
Useful Documents
Some useful links are given hereunder.
Algorithms used
The algorithms used are described in the following documents :
- STELA-NT-PRODUIT-7-CN
- STELA-NT-ETUDES-72-IMCCE01/02
- STELA-NT-ETUDES-86-IMCCE05/00
- STELA-NT-PRODUIT-134-CNES
Package Overview
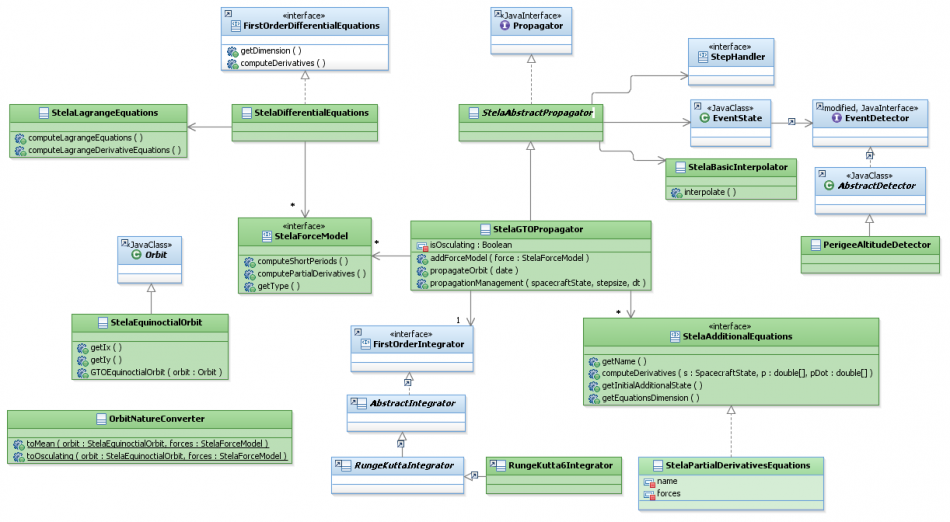
General architecture
This figure shows the general architecture of Stela GTO extrapolator.
Please note that not all implementations are present in the following diagram for the sake of clarity.
Features Description
Extrapolation
STELA propagator is built on-top of Patrius propagation framework. In particular it extends AbstractPropagator class and classic event detection can be performed.
Frames and Time Scales
STELA equations are integrated in CIRF frame. Reference system can be chosen by the user (among GCRF, CIRF, MOD).
Stela uses a simplified Precession/Nutation model (to perform GCRF <-> CIRF conversion) for faster computation. This model is called StelaPrecessionNutationModel.
STELA propagator uses a constant UTC- TAI shift. UTC - UT1 shift is considered as 0.
Implementation of frames and time scales configuration is detailed in next section.
Integrator
All integrators included can be used with STELA propagator. Nevertheless as the original tool has been validated with the 6^^th^^ order Runge-Kutta RungeKutta6Integrator, it is strongly recommanded to use it.
For more information on integrators, please refer to the [MAT_ODE_Home#HIntegrators ordinary differential equations] page.
Propagator
STELA propagator StelaGTOPropagator extends the abstract class StelaAbstractPropagator, this class is very close to the AbstractPropagator and implements the interface Propagator. Therefore it takes advantage of the Patrius propagation functionalities such as events detection, steps handling and it can use different first order integrators.
Propagation is performed using STELA mean elements.
Partial Derivatives
Partial Derivatives can be computed adding some additional equations to the propagator; the user willing to compute state partial derivatives can create an instance of StelaPartialDerivativesEquations and then add it to the propagator using the method addAdditionalEquations(StelaAdditionalEquations).
Their computation depends on the force model included in the propagator. Beware that some force models do not provide partial derivatives computation (see forces section below).
Partial derivatives are with respect to mean elements.
Time partial derivatives
Time partial derivatives can be retrieved from the propagator. Ask for time derivatives recording with:
StelaGTOPropagator.setStoreTimeDerivatives(boolean)
Then retrieve time partial derivatives using: StelaGTOPropagator.getTimeDerivativesList()
Time partial derivatives are with respect to mean elements.
StepHandlers
The step handlers in the STELA propagator should be used in the same way as the other propagators.
STELA step handlers provides mean elements as input.
EventDetectors
A specific PerigeeAltitudeDetector has been created to handle atmospheric reentry in the same fashion as Stela software. When using this detector, please enable the division of integration steps of last steps mecanism in the propagator.
Event detectors in STELA provide mean elements as input of init() and g() functions.
Additional Equations
A specific StelaAdditionalEquations interface has been created. This class is very close to the AdditionalEquations. A specific StelaAttitudeAdditionalEquations allows to build specific additional equation for attitude.
Forces
Forces can be chosen from these presented hereafter. Forces are simply added to the propagator calling the addForceModel() method. If no force is added, the propagation will follow a simple Keplerian motion.
Central Body
Various potential coefficients are implemented, hence can be chosen amongst the models implemented in the Library. Original STELA model is Grim_C5.
Zonal terms
Zonal terms can be computed using StelaZonalAttraction in a closed form of eccentricity up to J15. J2^^2^^ can also be taken into account. Partial Derivatives up to J7 and Short periodic terms are displayed as well.
Tesseral terms
Tesseral terms can be computed as well using StelaTesseralAttraction. Each effect of the tesseral harmonics terms which as a period greater than a user tunable value expressed as a multiple of the integrator step will be included. Maximum tesseral order is 15. Detailed algorithm can be found in STELA-NT-PRODUIT-134-CNES (see [ORB_GTO_Home#HUsefulDocuments useful documents]).
Solid tides
Solid tides from both Sun and Moon can be computed using SolidTidesAcc. Any Third body ephemerids can be used (implementing CelestialBody interface). Original STELA model is Meeus model. Short Periodic terms and Partial derivatives are not available.
Third Body
Third body perturbation can be computed using StelaThirdBodyAttraction. It includes Sun and Moon perturbation (although any celestial body perturbation can be taken into account since java interfaces are used). The theory is developped in Legendre polynomials hence the model can be customised through the degree of the polynomial used. Any Third body ephemerids can be used (implementing CelestialBody interface). Original STELA model is Meeus model. Short periodic terms and partial derivatives are available.
Solar radiation pressure (SRP)
Sun position is computed using provided Sun ephemerids model. Original STELA model is Meeus model.
Two different SRP models are available. A third one has been added to gather STELA features in one single model (perturbation taking into account eclipse, partial dérivatives not taking eclipses into account).
SRPPotential
This class compute the SRP force without eclipses. This can be used for a faster computation. Short periods are not implemented for this class.
SRPSquaring
The SRP is computed using Simpson Squaring (see [ORB_GTO_Home#HUsefulDocuments useful documents] for detailed algorithm). Sun eclipses are taken into account. Partial derivatives and short periods are not implemented for this class.
StelaSRPSquaring
This class implements the original Stela SRP force model: perturbation is computed using SRPSquaring class whereas partial derivatives are computed using SRPPotential class.
Atmospheric Drag
Atmospheric Drag is computed using a Simpson squaring method using StelaAtmosphericDrag class. Any atmospheric model can be used (implementing Atmosphere interface). Original STELA model is MSIS-00. For partial derivatives computation, two mecanisms are available (computation of variation of atmospheric density with respect either to altitude or to x, y, z position).
The drag coefficient used to compute the atmospheric drag can be constant or a function of spacecraft altitude.
Non-inertial contribution
Stela equations of motion are integrated in CIRF frame. The integration frame being non-inertial, acceleration accounting for non-inertial contribution can be added to the equations of motion. This is simply done by adding a NonInertialContribution instance to Stela force models. The user can choose the reference frame considered as inertial (between CIRF, GCRF and MOD). This contribution is computed thanks to Simpson squaring method. Partial derivatives are not computed.
Orbits
Conversions Mean <-> Osculating
Conversion is performed by taking into account provided forces short periodic terms. Integration of the équations of motion is performed in mean elements. Osculating elements are only used for user input/output and for computing atmospheric drag.
Stela Equinoctial Elements
Stela equinoctial elements slightly differ from Patrius equinoctial elements. They are defined as follow:
| Parameter | Definition |
|---|---|
| a | Semi-major axis |
| [math]\displaystyle{ \xi }[/math] | [math]\displaystyle{ \xi =\omega +\Omega+M }[/math] |
| ex | [math]\displaystyle{ e_x = e \cos( \Omega + \omega ) }[/math] |
| ey | [math]\displaystyle{ e_y = e \sin( \Omega + \omega ) }[/math] |
| ix | [math]\displaystyle{ i_x = \sin(i / 2) \cos( \Omega ) }[/math] |
| iy | [math]\displaystyle{ i_y = \sin(i / 2) \sin( \Omega ) }[/math] |
Getting Started
This section shows how to configure Stela dynamical model in Patrius. The example here below intends to have a configuration as close as possible to original STELA Software. Please keep in mind that a great majority of elements such as atmosphere or third bodies respect Patrius interfaces hence enabling the use of non-Stela specific elements.
Configuration: Frames and Time scales
Frames configuration
A specific frames configuration is provided to match STELA frames configuration. This configuration is used calling: FramesFactory.setConfiguration(FramesConfigurationFactory.getStelaConfiguration());
Time scales
STELA uses a constant UTC-TAI shift. This can be set using the following code:
TimeScalesFactory.clearUTCTAILoaders();
TimeScalesFactory.addUTCTAILoader(new MyUTCTAILoader());
With MyUTCTAILoader class being:
private class MyUTCTAILoader implements UTCTAILoader {
public MyUTCTAILoader() {}
public boolean stillAcceptsData() { return false; }
public void loadData(InputStream input, String name) throws IOException, ParseException, PatriusException { }
public SortedMap<DateComponents, Integer> loadTimeSteps() {
SortedMap<DateComponents, Integer> entries = new TreeMap<DateComponents, Integer>();
for (int i = 1969; i < 2200; i++) {
// UTC-TAI shift is set constant to 35s
// Here a UTC-TAI constant value is provided between years 1969 and year 2200. If propagation is performed out of these dates, more values should be provided
entries.put(new DateComponents(i, 1, 1), 35);
}
return entries;
}
public String getSupportedNames() { return ""; }
}
Propagator
The propagator is defined using a numerical integrator. Any fixed-stepsize integrator can be used. Adaptative stepsize integrator should not be used. The two last parameters in StelaGTOPropagator constructor define the behaviour of the propagator in case of re-entry problems (see StelaGTOPropagator Javadoc for more information). To sum-up, re-entry fails because of integration step which is too large (usually a day). As a result the reentry strategy is to reduce the integration step (division by 2) until some physical result is obtained. The first parameter "maxShiftIn" indicates the maximum number of integration steps STELA will try to correct (default is 5). The second parameter "minStepSizeIn" indicates the smallest step size allowed by the user (default is 1 second). If STELA could not find a suitable solution using the smallest allowed stepsize and in number of corrected integration step, an exception will be thrown. In the example bellow, the maximum number of integration step is 5 and the smallest allowed stepsize is 1s.
// Propagator
final Orbit initialOrbit = new StelaEquinoctialOrbit(7000000, 0, 0, 0, 0, 0, FramesFactory.getMOD(false), AbsoluteDate.J2000_EPOCH, Constants.EGM96_EARTH_MU);
final SpacecraftState initialState = new SpacecraftState(initialOrbit);
final double mass = 1000.;
final boolean isOsculating = false;
final double dt = 86400.;
final RungeKutta6Integrator rk6 = new RungeKutta6Integrator(dt);
final double maxShiftIn = 5; // Maximum number of integration steps STELA will try to correct
final double minStepSizeIn = 1; // Smallest step size allowed (in s)
final StelaGTOPropagator propagator = new StelaGTOPropagator(rk6, maxShiftIn, minStepSizeIn);
propagator.setInitialState(initialState, mass, isOsculating);
Force Model
The code example here after follows the creation of the propagator and adds different forces. When giving the PotentialCoefficientsProvider provider (see the [ORB_PHY_Home#HEarthpotential Earth Potential] section for more information) with Stela Software values, this is a normal Stela Software propagation, meaning that the partial derivatives of the state elements are not computed. Please look at the Javadoc associated with every [ORB_GTO_Home#HForcesModel Force Model] constructors to have an overall look at the offered possibilities.
// Force Model
// Earth potential model (coefficients C and S should have been added beforehand in GravityFieldFactory)
final PotentialCoefficientsProvider provider = GravityFieldFactory.getPotentialProvider();
// zonal perturbation
final int zonalOrder = 7;
final boolean isJ2SquareComputed = true;
final int shortPeriodsDegree = 2;
final int partialDerivativesZOnalOrder = 0;
final boolean isPartialDerivativesJ2SquareComputed = false;
final StelaZonalAttraction zonaux = new StelaZonalAttraction(provider, zonalOrder, isJ2SquareComputed, shortPeriodsDegree, partialDerivativesZOnalOrder, isPartialDerivativesJ2SquareComputed);
propagator.addForceModel(zonaux);
// tesseral perturbation
final int tesseralOrder = 7;
final int qmaxKaula = 5;
final double integrationStep = 86400.;
final int maxIntegrationStep = 2;
final StelaTesseralAttraction tesseraux = new StelaTesseralAttraction(provider, tesseralOrder, qmaxKaula, integrationStep, maxIntegrationStep);
propagator.addForceModel(tesseraux);
// atmospheric drag
final CelestialBody sun = new MeeusSun(MODEL.STELA);
// earth- stela values
final double f = 0.29825765000000E+03;
final double ae = 6378136.46;
// Constant solar activity:
final ConstantSolarActivity solarActivity = new ConstantSolarActivity(140, 15);
// Atmosphere:
final Atmosphere atmosphere = new MSISE2000(new ClassicalMSISE2000SolarData(solarActivity), new OneAxisEllipsoid(ae, 1 / f, FramesFactory.getTIRF()), sun);
final double dragCoef = 2.2;
final double dragArea = 10.;
final StelaCd cd = new StelaCd(dragCoef);
final StelaAeroModel sp = new StelaAeroModel(mass, cd, dragArea, atmosphere, 50);
final StelaAtmosphericDrag atmosphericDrag = new StelaAtmosphericDrag(sp, atmosphere, 33, 6378000, 2500000, 2);
propagator.addForceModel(atmosphericDrag);
// SRP
final double refCoef = 1.5;
final double refArea = 10.;
final StelaSRPSquaring srpStela = new StelaSRPSquaring(mass, refArea, refCoef, 11, sun);
propagator.addForceModel(srpStela);
// 3rd bodies
// SUN
final StelaThirdBodyAttraction sunPerturbation = new StelaThirdBodyAttraction(sun, 4, 0, 2);
propagator.addForceModel(sunPerturbation);
// MOON
final CelestialBody moon = new MeeusMoonStela(6378136.46);
final StelaThirdBodyAttraction moonPerturbation = new StelaThirdBodyAttraction(moon, 4, 0, 2);
propagator.addForceModel(moonPerturbation);
// Non-inertial contribution (with GCRF reference system)
final NonInertialContribution nonInertialContribution = new NonInertialContribution (11, FramesFactory.getGCRF());
propagator.addForceModel(nonInertialContribution);
// Solid tides
final SolidTidesAcc solidTidesAcc = new SolidTidesAcc(sun, moon);
propagator.addForceModel(solidTidesAcc);
Ephemeris Manager
When the user needs to record all the ephemeris of the propagation, the following code can be implemented. Note that when recording partial derivatives of the state elements as well, the handler is a little bit trickier and will be presented in another paragraph.
// Ephemeris Manager
final List<SpacecraftState> ephemeris = new ArrayList<SpacecraftState>();
PatriusFixedStepHandler handler = new PatriusFixedStepHandler() {
@Override
public void init(final SpacecraftState s0, final AbsoluteDate t) {
}
@Override
public void handleStep(final SpacecraftState currentState, final boolean isLast) throws PropagationException {
ephemeris.add(currentState);
propagator.resetInitialState(currentState);
}
};
propagator.setMasterMode(dt, handler);
Reentry altitude detector
The following detector was created to stop the simulation when the perigee of the orbit is below a chosen re-entry altitude. Please note that you can add other Patrius detectors following the same method.
// reentry altitude
final double reentryAltitude = 80000;
final double earthRadius = 6378136.46;
final double maxCheck = dt;
final double threshold = 0.5;
final OrbitNatureConverter orbConv = new OrbitNatureConverter(propagator.getForceModels());
final PerigeeAltitudeDetector perDet = new PerigeeAltitudeDetector(maxCheck, threshold, reentryAltitude, earthRadius, orbConv);
propagator.addEventDetector(perDet);
Propagation
Propagation is performed in the same manner as with any other propagator:
propagator.propagate(initialState.getDate(), endDate);
Partial Derivatives
The partial derivatives as well as the short periods parameters are handled when creating the different forces. When willing to compute the partial derivatives, one should add the additional equations to the propagator in the following way :
final StelaPartialDerivativesEquations pd = new StelaPartialDerivativesEquations(
propagator.getGaussForceModels(), propagator.getLagrangeForceModels(), 1, propagator);
propagator.addAdditionalEquations(pd);
The new additional states corresponding to these equations should be added to the spacecraftstate as well:
// get a new spacecraftstate adding the new additional states to the initial one:
final SpacecraftState updatedState = pd.addInitialAdditionalState(initialState);
// link the updated spacecraftstate to the propagator:
propagator.resetInitialState(updatedState);
Please note that this step must be done AFTER adding all the forces to the propagator. The stepHandler will then be a bit more complex; all the matrix manipulations are done in order to have a similar presentation to Stela and are not at all compulsory.
final List<SpacecraftState> ephemeris = new ArrayList<SpacecraftState>();
final List<double[]> parDer = new ArrayList<double[]>();
final double[] add1 = { 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1};
parDer.add(add1);
PatriusFixedStepHandler handler = new PatriusFixedStepHandler() {
@Override
public void init(final SpacecraftState s0, final AbsoluteDate t) {
}
@Override
public void handleStep(final SpacecraftState currentState, final boolean isLast)
throws PropagationException {
ephemeris.add(currentState);
double[] addState;
try {
addState = currentState.getAdditionalState("PARTIAL_DERIVATIVES");
// matrix reshapping
double[][] mat = new double[6][6];
JavaMathAdapter.vectorToMatrix(addState.clone(), mat);
double[][] newMat = new double[mat.length][mat[0].length];
double[][] newMat2 = new double[mat.length][mat[0].length];
for (int i = 0; i < mat.length; i++) {
newMat[i][0] = mat[i][0];
newMat[i][1] = mat[i][2];
newMat[i][2] = mat[i][3];
newMat[i][3] = mat[i][4];
newMat[i][4] = mat[i][5];
newMat[i][5] = mat[i][1];
}
for (int i = 0; i < newMat[0].length; i++) {
newMat2[0][i] = newMat[0][i];
newMat2[1][i] = newMat[2][i];
newMat2[2][i] = newMat[3][i];
newMat2[3][i] = newMat[4][i];
newMat2[4][i] = newMat[5][i];
newMat2[5][i] = newMat[1][i];
}
double[] addstate2 = new double[addState.clone().length];
JavaMathAdapter.matrixToVector(newMat2, addstate2, 0);
parDer.add(addstate2);
} catch (PatriusException e) {
e.printStackTrace();
}
propagator.resetInitialState(currentState);
}
};
Contents
Interfaces
| Interface | Summary | Javadoc |
|---|---|---|
| StelaForceModel | Interface for all the forces that can be used. | ... |
| StelaAdditionalEquations | Interface representing additional equations. | ... |
Classes
Stela
| Class | Summary | Javadoc |
|---|---|---|
| JavaMathAdapter | Collection of mathematical methods, mainly matrices computation. | ... |
| PerigeeAltitudeDetector | Detector of perigee altitude. | ... |
| StelaSpacecraftFactory | Builds a simplified assembly for SRP use. | ... |
Bodies
| Class | Summary | Javadoc |
|---|---|---|
| Classes computing earth rotation and earth rotation rate. | ... | |
| GeodPosition | Classes computing geodesic position. | ... |
| MeeusMoonStela | Moon representation with STELA adaptation of meeus algorithm. | ... |
Forces
| Class | Summary | Javadoc |
|---|---|---|
| AbstractStelaLagrangeContribution | Classes that extends this Abstract class will be known as Lagrange equations users. | ... |
| AbstractStelaGaussContribution | Classes that extends this Abstract class will know Gauss equations and its derivatives. | ... |
| StelaLagrangeEquations | Class computing Lagrange planetary equations. | ... |
| Squaring | Class implementaing Simpson squaring method. | ... |
Atmospheres
| Class | Summary | Javadoc |
|---|---|---|
| MSISE2000 | Classe de modélisation pour le modèle d'atmosphère MSIS00 (ex MSIS00Adapter du code de STELA). | ... |
Drag
| Class | Summary | Javadoc |
|---|---|---|
| StelaAtmosphericDrag | Class computing atmospheric drag terms using Simpson Squaring method. | ... |
| StelaAeroModel | Class containing the STELA algorithms for drag acceleration and partial derivatives computation, for a spherical spacecraft. | ... |
| StelaCd | Class managing the variable Cd aerodynamic coefficient. | ... |
Gravity
| Class | Summary | Javadoc |
|---|---|---|
| StelaZonalAttraction | Class computing zonal terms | ... |
| StelaTesseralAttraction | Class computing tesseral terms | ... |
| TesseralQuad | Class computing quad terms for tesseral perturbation computation | ... |
| StelaThirdBodyAttraction | Class computing Third bodies terms. | ... |
Radiation
| Class | Summary | Javadoc |
|---|---|---|
| SRPPotential | Class computing SRP terms as a potential. | ... |
| SRPSquaring | Class computing SRP terms using Simpson Squarring method. | ... |
| StelaSRPSquaring | Class computing SRP terms using Simpson Squarring method. The partial derivatives are computed using an inner SRPPotential field. | ... |
Non-inertial contribution
| Class | Summary | Javadoc |
|---|---|---|
| NonInertialContribution | Class computing non-inertial contribution. | ... |
Tides
| Class | Summary | Javadoc |
|---|---|---|
| SolidTidesAcc | Class computing solid tides perturbation (Moon and Sun contributions) | ... |
Orbits
| Class | Summary | Javadoc |
|---|---|---|
| OrbitNatureConverter | Compute the mean to osculating tranformation with a force model and vice versa. | ... |
| StelaEquinoctialOrbit | Implements Stela particular type of parameters. | ... |
| JacobianConverter | Converts Jacobian matrices between equinoctial and cartesian elements. | ... |
Propagation
| Class | Summary | Javadoc |
|---|---|---|
| StelaAbstractPropagator | Adaptation of AbstractPropagator for semi-analytical propagation | ... |
| StelaBasicInterpolator | Basic Linear interpolator for StelaAbstractPropagator | ... |
| StelaGTOPropagator | Propagator for the GTO extrapolator. | ... |
| StelaDifferentialEquations | Sums all the perturbation from the force model and gives the equation to the integrator. | ... |
| StelaPartialDerivativesEquations | Class representing partial derivatives equations. | ... |
| StelaAttitudeAdditionalEquations | Abstract class containing attitude differential equations to be used in a Stela GTO propagator. | ... |