User Manual 3.4.1 Angles and Intervals

Introduction

Scope

This section describes how angles, intervals and angle intervals are defined and used in the PATRIUS library.

Javadoc

The angle-related objects are available in the package fr.cnes.sirius.patrius.utils in the PATRIUS library. The class defining an interval end point, though, is in the package org.orekit.utils from orekit-addons.

Library	Javadoc
Patrius	Package fr.cnes.sirius.patrius.utils
Orekit addons	Package org.orekit.utils

Links

None as of now.

Useful Documents

None as of now.

Package Overview

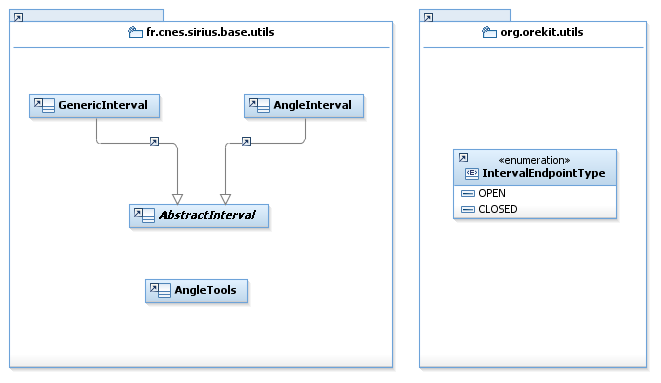
The package org.orekit.utils contains the class IntervalEndPoint that defines the type of boundary (CLOSED, OPEN) of an interval end.

The package fr.cnes.sirius.patrius.utils contains the actual angle-related classes.

Features Description

Generic intervals

An interval is made of two endpoints, and each endpoint may be closed or opened.

This is the most generic implementation of intervals : the class GenericInterval<T>. The enumeration provides the endpoint types : CLOSED and OPEN.

This class is meant to be used as a parent class for all intervals implementations.

This class makes no assumption on the nature of the parameter class T, so it may create intervals of anything- but the functionality for this class is limited (we only have getters for the endpoints values, and their type). That's why it's meant to be used as a parent class.

The class is immutable, in the sense that the endpoints objects are set at the interval creation.

Mutable types should not be used as endpoint value types!

Examples :

       final IntervalEndpointType lowType = IntervalEndpointType.OPEN;
        final Double lowValue = new Double(34.56);
        final IntervalEndpointType upType = IntervalEndpointType.CLOSED;
        final Double upValue = new Double(-2.3e34);
        // Note the order of values is off : this class cannot enforce an order
        final GenericInterval<Double> tgi = new GenericInterval<Double>(lowType, lowValue, upValue, upType);
        final Double gLow = tgi.getLowerData();
        assertTrue(gLow.equals(lowValue));

Please see the Javadoc for more information.

Example with doubles: interval [1.0, 2.0[ :

GenericInterval<Double> interval = new GenericInterval<Double>(IntervalEndpointType.CLOSED, 1.0, 2.0, IntervalEndpointType.OPEN);

Comparable intervals

This implementation of intervals,

ComparableInterval<T extends Comparable<T>>

, is for types implementing the Comparable interface ( for instance : Integer, Double).

This implementation inherits from GenericInterval<T>; in addition to inherited capabilities, it enforces a proper order on the lower and upper endpoints. A ComparableInterval can also tell :

if a given value is inside an interval
if an interval is inside another
if two intervals overlap

Please see the Javadoc for more information.

Angle intervals

The AngleInterval class represents an interval of doubles that shall be used to deal with angles. It contains the end points values and types (enum OPENED and CLOSED, class IntervalEndPointType), the mid value (“reference”) and the interval length.

Angle tools

This class is a toolbox containing static methods to perform operations on angles, for instance :

angleInInterval : sets an angle in an interval modulo 2Pi

Due to numerical quality issues, the algorithm is the following :

- If the interval is of the form [a, a + 2Pi[, then

    if x < a and x + 2Pi >= a + 2Pi, the angle is set to a (numerical quality issue due to the non-iqual repartition of real values around lower and upper boundaries)
    if x = 2Pi, the angle is set to a

- If the interval is of the form ]a, a + 2Pi], then

    if x > a + 2Pi and x – 2Pi <= a, the angle is set to a + 2Pi (numerical quality issue due to the non-iqual repartition of real values around lower and upper boundaries)
    if x = a, the angle is set to a + 2Pi

- Else

    if x < a, the angle is set to x + 2Pi
    if x > a + 2Pi, the angle is set to x- 2Pi
    else the angle is x

angle comparisons
supplementary, complementary angles computation

Getting Started

Comparable intervals

Hereunder is given a code example illustrating how the Modèle:Code language="java"ComparableIntervalModèle:/code object behaves:

(% class="box code" %) (((

       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double d1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(-4.44);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double d2 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(2.22);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double d3 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(6.23);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double d4 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(8.72);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) IntervalEndpointType open (% style="color: rgb(102, 102, 102);" %)=(%%) IntervalEndpointType(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)OPEN(% style="color: rgb(102, 102, 102);" %);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) IntervalEndpointType closed (% style="color: rgb(102, 102, 102);" %)=(%%) IntervalEndpointType(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)CLOSED(% style="color: rgb(102, 102, 102);" %);(%%)
       (% style="color: rgb(64, 128, 128);" %)~/~/ Interval : [ -4.44 ; 2.22 [

(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>(%%) ti1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>((%%)closed(% style="color: rgb(102, 102, 102);" %),(%%) d1(% style="color: rgb(102, 102, 102);" %),(%%) d2(% style="color: rgb(102, 102, 102);" %),(%%) open(% style="color: rgb(102, 102, 102);" %));(%%)

       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double inside1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(-4.44);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double inside2 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(-2.24);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double outside1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(-0.2313E96);(%%)
       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) Double outside2 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) Double(% style="color: rgb(102, 102, 102);" %)(-4.45);(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)((%%)ti1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)contains(% style="color: rgb(102, 102, 102);" %)((%%)inside1(% style="color: rgb(102, 102, 102);" %)));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)((%%)ti1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)contains(% style="color: rgb(102, 102, 102);" %)((%%)inside2(% style="color: rgb(102, 102, 102);" %)));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)(!(%%)ti1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)contains(% style="color: rgb(102, 102, 102);" %)((%%)outside1(% style="color: rgb(102, 102, 102);" %)));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)(!(%%)ti1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)contains(% style="color: rgb(102, 102, 102);" %)((%%)outside2(% style="color: rgb(102, 102, 102);" %)));(%%)
       (% style="color: rgb(64, 128, 128);" %)~/~/ Two open overlapping intervals

(%%) (% style="color: rgb(64, 128, 128);" %)~/~/ ] d1 ; d3 [ (%%) (% style="color: rgb(64, 128, 128);" %)~/~/ ...] d2 ; d4 [ (%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>(%%) ovo1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>((%%)open(% style="color: rgb(102, 102, 102);" %),(%%) d1(% style="color: rgb(102, 102, 102);" %),(%%) d3(% style="color: rgb(102, 102, 102);" %),(%%) open(% style="color: rgb(102, 102, 102);" %));(%%)

       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>(%%) ovo2 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>((%%)open(% style="color: rgb(102, 102, 102);" %),(%%) d2(% style="color: rgb(102, 102, 102);" %),(%%) d4(% style="color: rgb(102, 102, 102);" %),(%%) open(% style="color: rgb(102, 102, 102);" %));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)((%%)ovo1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)overlaps(% style="color: rgb(102, 102, 102);" %)((%%)ovo2(% style="color: rgb(102, 102, 102);" %)));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)((%%)ovo2(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)overlaps(% style="color: rgb(102, 102, 102);" %)((%%)ovo1(% style="color: rgb(102, 102, 102);" %)));(%%)
       (% style="color: rgb(64, 128, 128);" %)~/~/ Two closed intervals, first includes second

(%%) (% style="color: rgb(64, 128, 128);" %)~/~/ [ d1 .....;..... d4 ] (%%) (% style="color: rgb(64, 128, 128);" %)~/~/ .....[ d2 ; d3 ] (%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>(%%) clos1 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>((%%)closed(% style="color: rgb(102, 102, 102);" %),(%%) d1(% style="color: rgb(102, 102, 102);" %),(%%) d4(% style="color: rgb(102, 102, 102);" %),(%%) closed(% style="color: rgb(102, 102, 102);" %));(%%)

       (% style="font-weight: bold; color: rgb(0, 128, 0);" %)final(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>(%%) clos2 (% style="color: rgb(102, 102, 102);" %)=(%%) (% style="font-weight: bold; color: rgb(0, 128, 0);" %)new(%%) ComparableInterval(% style="color: rgb(102, 102, 102);" %)<(%%)Double(% style="color: rgb(102, 102, 102);" %)>((%%)closed(% style="color: rgb(102, 102, 102);" %),(%%) d2(% style="color: rgb(102, 102, 102);" %),(%%) d3(% style="color: rgb(102, 102, 102);" %),(%%) closed(% style="color: rgb(102, 102, 102);" %));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)((%%)clos1(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)includes(% style="color: rgb(102, 102, 102);" %)((%%)clos2(% style="color: rgb(102, 102, 102);" %)));(%%)
       assertTrue(% style="color: rgb(102, 102, 102);" %)(!(%%)clos2(% style="color: rgb(102, 102, 102);" %).(% style="color: rgb(125, 144, 41);" %)includes(% style="color: rgb(102, 102, 102);" %)((%%)clos1(% style="color: rgb(102, 102, 102);" %)));

)))

Class	Summary	Javadoc
IntervalEndpointType	Defines an interval end point as OPEN or CLOSED.	...
AngleInterval	Implements an interval of angles, taking angles' modulus into account.	...
AngleTools	Provides several angle-related utility methods.	...
GenericInterval	Implements a generic interval.	...
AbsoluteDateInterval	This class implements an interval based on the AbsoluteDate class using the ComparableInterval class.	...
ComparableInterval	The class describe an interval of Comparable data.	...

Angle intervals

Two constructors are available for an AngleInterval instance :

One needing directly the end points values and types. Its signature is in the writing order. For example, to create [0.0, 2PI[ :

AngleInterval angleInterval1 = new AngleInterval(IntervalEndpointType.CLOSED, 0.0,
   MathUtils.TWO_PI, IntervalEndpointType.OPEN);

One needing the reference and length values, and the end points nature. Here, the signature is : “reference”, “length”, “lower end point type”, “upper end point type”. To create [-PI, PI[ :

AngleInterval angleInterval1 = new AngleInterval(0.0, MathUtils.TWO_PI,
   IntervalEndpointType.CLOSED, IntervalEndpointType.OPEN);

Those constructors throw an exception « MathIllegalArgumentException » if the interval is not valid. It is considered not valid if :

The length is strictly greater than 2PI
The length is equal to 2PI and both end points are “closed”
The length is negative
The length is zero and at least one end point is opened (an interval with only one double in it is accepted)

Those intervals are impossible to modify once created : they have no setters. To get an interval with different values, a new one shall be constructed.

Angle tools

The method "angleInInterval"

The method « angleInInterval » computes the (2PI) modulus of an angle (given as a double) in an angle interval (AngleInterval object) :

If a (2PI) modulus of the input angle exists in the interval, its value is returned. Because the angles have a maximum length of 2PI with at least an open end point, there can be only one solution.
If no value in the interval is a solution, it means the operation is impossible with the given inputs, and a « MathIllegalArgumentException » is thrown.

Use example :

try {
// Angle
double angle = 6*FastMath.PI;
 
// Interval creation 
AngleInterval angleInterval = new AngleInterval(IntervalEndpointType.OPEN, 
- MathUtils.HALF_PI, MathUtils.HALF_PI, IntervalEndpointType.OPEN);
 
// angle in interval
double result = AngleTools.angleInInterval(angle, angleInterval);
}
catch (MathIllegalArgumentException e) {
 // correct catch!
}

« result » value is here 0.0 : the modulus of 6PI in ]-PI/2,-PI/2[

Comparisons methods

The comparison methods available in the AngleTools class are the same as the one for doubles in the « Comparators » class : relative comparisons using a default epsilon. Input angles are only expressed in the input interval before the comparison.

If the computation in the interval of one of the input angles is not possible, a « MathIllegalArgumentException » is thrown.

Use example :

try {
// Angle
double angle1 = 6*FastMath.PI;
double angle2 = 4*FastMath.PI + 0.1;
 
// Interval creation 
AngleInterval angleInterval = new AngleInterval(IntervalEndpointType.OPEN, 
- MathUtils.HALF_PI, MathUtils.HALF_PI, IntervalEndpointType.OPEN);
 
// angle in interval
boolean isLowerOrEqual = AngleTools.lowerOrEqual(angle1, angle2, angleInterval);
}
catch (MathIllegalArgumentException e) {
 // correct catch !
}

Both angles are here computable in the given interval. The first one is lower than the second once in the interval : the returned result is “true”

Supplementary, complementary and opposite angles

The tools box AngleTools proposes the methods to compute supplementary (method supplementaryAngle), complementary (method complementaryAngle) and opposite (method oppositeAngle) angles, taking into account an angle interval (of the type AngleInterval previously described)

Those methods first compute a common supplementary, complementary or opposite angle, and then try to express the result in the given interval. If this last operation is not possible, an exception is thrown (MathIllegalArgumentException).

Use example :

try {
 // Interval creation
 AngleInterval angleInterval = new AngleInterval(IntervalEndpointType.OPEN, 
- MathUtils.HALF_PI, MathUtils.HALF_PI, IntervalEndpointType.OPEN);
 
 // computation
 double angle = 3.0/4.0*FastMath.PI + 6.0*FastMath.PI;
 double res = AngleTools.supplementaryAngle(angle, angleInterval);
 
}
catch (MathIllegalArgumentException e) {
 // correct catch !
 
}

The result is here computable, its value is PI/4.

User Manual 3.4.1 Angles and Intervals

Sommaire

Introduction

Scope

Javadoc

Links

Useful Documents

Package Overview

Features Description

Generic intervals

Comparable intervals

Angle intervals

Angle tools

Getting Started

Comparable intervals

Contents

Interfaces

Classes

Angle intervals

Angle tools

The method "angleInInterval"

Comparisons methods

Supplementary, complementary and opposite angles

Menu de navigation

Outils personnels

Espaces de noms

Variantes

Affichages

Plus

Rechercher

PATRIUS

Evolutions

User Manual

Tutorials

Links

Navigation

Outils

Imprimer / exporter